Στη Γεωμετρία του Ευκλείδη, δύο τρίγωνα θεωρούνται ίσα όταν με κατάλληλη “μετατόπιση” συμπίπτουν. Εδώ, μετατόπιση σημαίνει αλλαγή της θέσης του τριγώνου, “άκαμπτα”, χωρίς, δηλαδή, να αλλάζουν οι αποστάσεις για οποιαδήποτε δύο σημεία του.
Πρακτικά, η μετατόπιση ενός τριγώνου, με την έννοια που περιγράφηκε παραπάνω, μπορεί να αναπαρασταθεί με τη βοήθεια ενός διαφανούς χαρτιού, αποτυπώνοντας, πάνω σ’ αυτό, το τρίγωνο κι έπειτα μεταφέροντας, στρέφοντας ή, ακόμη, αναστρέφοντας το χαρτί. Σε κάθε περίπτωση, από τη σκοπιά της Γεωμετρίας, το αποτυπωμένο τρίγωνο παραμένει αναλλοίωτο.
Αν ένα τρίγωνο μετατοπιστεί και οι κορυφές του ταυτιστούν, μία προς μία, με τις κορυφές ενός άλλου τριγώνου, τότε, τα δύο συμπίπτοντα τρίγωνα θα έχουν τα αντίστοιχα κύρια και δευτερεύοντα στοιχεία τους ίσα, ένα προς ένα, δηλαδή, τις αντίστοιχες πλευρές τους ίσες, μία προς μία, τις αντίστοιχες γωνίες τους ίσες, μία προς μία, τις αντίστοιχες διαμέσους τους ίσες, μία προς μία, κ.τ.λ..
Αντίστροφα, ενδιαφέρον παρουσιάζει η διερεύνηση κριτηρίων, βάσει των οποίων μπορεί κανείς, προκαταβολικά, να είναι σε θέση να αποφανθεί αν δύο τρίγωνα είναι ή όχι ίσα. Πρόκειται για τα Κριτήρια Ισότητας Τριγώνων τα οποία, αρχικά, θα μπορούσαν να αναζητηθούν μεταξύ κατάλληλων συνθηκών σε σχέση με τα κύρια στοιχεία των τριγώνων (πλευρές – γωνίες).
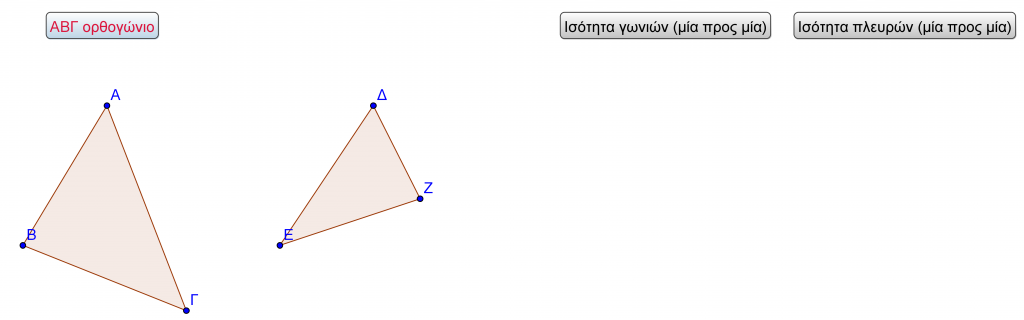
Δραστηριότητα: Στο ακόλουθο γραφικό,
με το οποίο μπορείτε να αλληλεπιδράσετε, παριστάνονται δύο τρίγωνα ΑΒΓ και ΔΕΖ. Το ΑΒΓ μπορεί να επιλεγεί είτε τυχαίο είτε ορθογώνιο.
Να επαναπροσδιορίσετε ορισμένα από τα στοιχεία του ΔΕΖ ώστε το τρίγωνο να μετασχηματιστεί σε τρίγωνο ίσο με το ΑΒΓ.
- Να δοκιμάσετε, πάλι, αλλάζοντας, ενδεχομένως, τα αρχικά τρίγωνα. Να επιχειρήσετε να τροποποιήσετε κάποιες απ’ τις συνθήκες που επιλέξατε.
- Να αφαιρέσετε τυχόν περιττές συνθήκες και να καταγράψετε τις απαραίτητες.
- Να βεβαιωθείτε ότι η ισότητα των τριγώνων επιβάλλεται απ’ τις συνθήκες, που κάθε φορά επιλέγετε, κι ότι δεν είναι απλή σύμπτωση.
- Πειραματιστείτε …
Ανακαλύψατε κάποιο κριτήριο;
Άσκηση 1: Να προσπαθήσετε να διατυπώσετε κατάλληλες συνθήκες σε σχέση και με τα δευτερεύοντας στοιχεία των τριγώνων (διάμεσοι, ύψη, διχοτόμοι), ώστε δύο τρίγωνα να είναι ίσα.
Άσκηση 2: Η έννοια της ισότητας επεκτείνεται με τον ίδιο τρόπο και στα τετράπλευρα. Να προσπαθήσετε να διατυπώσετε κριτήριο ισότητας τετραπλεύρων αξιοποιώντας κάποιο από τα κριτήρια ισότητας τριγώνων που ανακαλύψατε προηγουμένως.
(Υπόδειξη: Βρείτε πρώτα κατάλληλα τρίγωνα που “κρύβονται” στα τετράπλευρά σας.)
Copyright © 2013. Με την επιφύλαξη όλων των δικαιωμάτων.