Ο Θαλής ο Μιλήσιος γεννήθηκε στη Μίλητο της Μ. Ασίας περίπου το 624 π.Χ.. Ήταν ο πρώτος απ’ τους επτά σοφούς της αρχαιότητας, ο πρώτος Έλληνας φιλόσοφος και, ίσως, ο πρώτος μαθηματικός, αφού εισήγαγε την απόδειξη στη Γεωμετρία. Θεωρείται ότι διδάχθηκε Γεωμετρία στον τόπο γέννησής της, δηλαδή στην Αίγυπτο.
Ποια ανάγκη, όμως, είχε ωθήσει τους Αιγύπτιους στη δημιουργία των πρώτων γεωμετρικών εννοιών; Η απάντηση πρέπει να αναζητηθεί σ’ ένα πρόβλημα πρακτικής φύσης. Οι Αιγύπτιοι κάθε φορά που πλημμύριζε ο Νείλος, έπρεπε να αποκαταστήσουν τα σύνορα των ιδιοκτησιών τους. Αυτό τους οδήγησε στο να ανακαλύψουν ένα σύνολο εμπειρικών κανόνων με πρακτικές εφαρμογές, κυρίως, σε μετρήσεις επί του εδάφους:
«γη» + «μέτρηση» = «γεωμετρία».
Ο Θαλής έμαθε τις πρώτες γεωμετρικές τεχνικές από τους Αιγύπτιους ιερείς και, προχωρώντας ένα βήμα πιο πέρα, τις μετέφερε στο χαρτί, αντικαθιστώντας αντικείμενα της εμπειρίας όπως πάσσαλοι, σχοινιά, κυκλικές περιφέρειες εδαφικών εκτάσεων, από σημεία, ευθύγραμμα τμήματα, ευθείες γραμμές και κύκλους. Έτσι, θεμελίωσε το υπόβαθρο πάνω στο οποίο έπρεπε να γίνει η καταγραφή αλλά και η αιτιολόγηση αυτών των κανόνων. Με την επιστροφή του στην αρχαία Ελλάδα, οι εμπειρικοί κανόνες των Αιγυπτίων άρχισαν να μετασχηματίζονται στα πρώτα γεωμετρικά θεωρήματα.
Ενδεικτικά, ας αναφερθεί ότι αν και οι πέντε προτάσεις που ακολουθούν πρέπει να ήταν γνωστές στους Αιγύπτιους, ωστόσο, οι αποδείξεις τους αποδίδονται από ορισμένους ιστορικούς των Μαθηματικών στον Θαλή:
- Κάθε διάμετρος χωρίζει τον κύκλο σε δύο ίσα τόξα (ημικύκλια).
- Οι προσκείμενες στη βάση γωνίες ισοσκελούς τριγώνου είναι ίσες.
- Η εγγεγραμμένη γωνία που βαίνει σε ημικύκλιο είναι ορθή.
- Οι κατακορυφήν γωνίες είναι ίσες.
- Αν μία πλευρά ενός τριγώνου είναι ίση με μία πλευρά ενός δεύτερου τριγώνου και οι προσκείμενες γωνίες στις πλευρές αυτές είναι ίσες μία προς μία, τότε τα δύο τρίγωνα είναι ίσα.
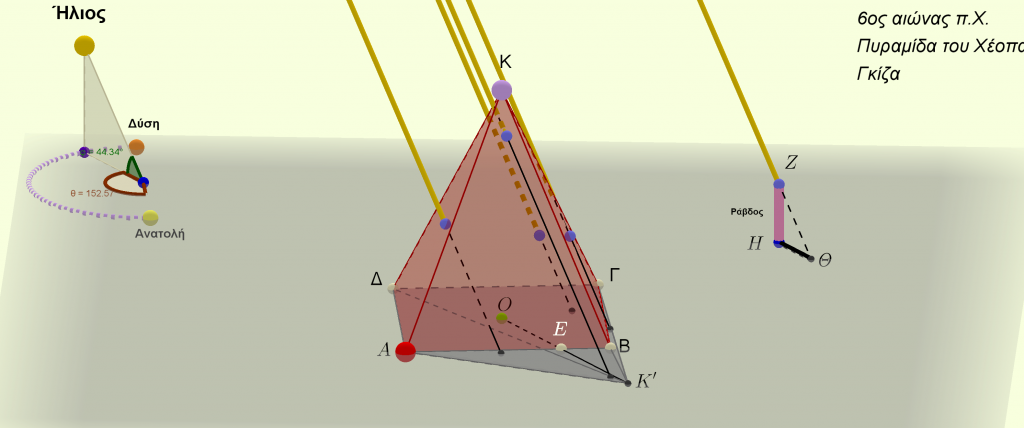
Ο αρχαίος Έλληνας ιστορικός Διογένης ο Λαέρτιος αναφέρει ότι ο Θαλής, κατά τη διάρκεια της παραμονής του στην Αίγυπτο, κατάφερε να μετρήσει το ύψος της Πυραμίδας του Χέοπα. Σύμφωνα με εκείνον, ο Θαλής πραγματοποίησε τη μέτρηση χρησιμοποιώντας τη σκιά του εαυτού του, παρατηρώντας ότι αν κάποια μέρα η σκιά του γινόταν ίση με το ύψος του, τότε το ίδιο θα συνέβαινε και με τη σκιά του ύψους της πυραμίδας.
Επομένως, η μέτρηση του ύψους της πυραμίδας μπορούσε, τελικά, να γίνει στο έδαφος. Όμως, ποια γωνία θα σχημάτιζαν, τότε, οι ακτίνες του ήλιου με το έδαφος; Θα μπορούσε να συμβεί κάτι τέτοιο; Αν ναι, πότε; Τι προσανατολισμό έπρεπε να έχει η σκιά της πυραμίδας, ώστε να είναι δυνατό να μετρηθεί η σκιά του ύψους της; Πώς μπορούσε ο Θαλής, έστω και στο έδαφος, να μετρήσει τη σκιά του ύψους της πυραμίδας, αφού ένα μέρος της σκιάς του δεν ήταν ορατό;
Το ακόλουθο γραφικό, με το οποίο μπορείτε να αλληλεπιδράσετε, βοηθά στο να κατανοηθούν και να απαντηθούν, εν μέρει, τα προηγούμενα ερωτήματα. Έχετε υπόψη σας, ότι μετακινώντας, κατάλληλα, την κορυφή 
της πυραμίδας 
και το άκρο 
του ευθύγραμμου τμήματος 
, αλλάζουν οι διαστάσεις της πυραμίδας και του τμήματος. Επίσης, χρησιμοποιώντας το σημείο ελέγχου του ήλιου, μπορείτε να αλλάξετε την κατεύθυνσή των ακτίνων φωτός. Ακόμη, για να περιστραφεί το γραφικό, αρκεί να κρατηθεί το δεξί πλήκτρο του ποντικιού πατημένο και να μετακινηθεί ο κέρσορας. Τέλος, μπορείτε να αλλάξετε τη θέση της πυραμίδας και του τμήματος μετακινώντας τον κέρσορα του ποντικιού, αφού κρατήσετε πατημένο το πλήκτρο “Shift”.
Στο σημείο αυτό πρέπει να σημειωθούν τα εξής:
Πρώτα απ’ όλα ότι το γεωγραφικό πλάτος της Γκίζας, όπου βρίσκεται η πυραμίδα, είναι 29ο 57′ βόρεια του Ισημερινού. Αυτό επιτρέπει στις ακτίνες του ήλιου να σχηματίζουν γωνία 45ο με το έδαφος, το μεσημέρι, δύο φορές κάθε χρόνο (μπορείτε να δείτε τις ακριβείς ημερομηνίες που συμβαίνει αυτό, από εδώ). Αυτή η ειδική τιμή τής γωνίας διαδραμάτισε σημαντικό ρόλο στην προσπάθεια του Θαλή, διότι σ’ αυτήν την περίπτωση το μήκος της σκιάς ενός αντικειμένου γίνεται ίσο με το ύψος του.
Ακόμη, η πυραμίδα είχε κατασκευαστεί, έτσι, ώστε η μία έδρα της, στο γραφικό η 
, να είναι στραμμένη προς την ανατολή. Αυτό σημαίνει ότι τα μεσημέρια, όπου ο ήλιος «βλέπει» την έδρα 
, οι ακτίνες του ήλιου είναι κάθετες στην πλευρά 
της βάσης της πυραμίδας, γι’ αυτό, τότε, η σκιά της είναι το ισοσκελές τρίγωνο 
.
Άρα, το μεσημέρι μιας τέτοιας μέρας, όπου η σκιά του Θαλή γινόταν ίση με το ύψος του, θα είχαμε,
,
με τα επιμέρους μεγέθη να μπορούν, πλέον, να μετρηθούν.
Την εποχή της κατασκευής της, το 2560 π. Χ., η πυραμίδα του Χέοπα είχε ύψος 146,6 μέτρα. Για 3800 χρόνια ήταν το ψηλότερο μνημείο στον κόσμο. Σήμερα γνωρίζουμε ότι το ύψος της είναι 138,8 μέτρα, περίπου, αφού εκτός από καθίζηση έχει υποστεί και φθορές στο εξωτερικό της. Ο Θαλής πέθανε περίπου το 547 π.Χ..
Όμως, ό,τι συμβαίνει με την ύλη, δε συμβαίνει με το ανθρώπινο πνεύμα. Η βασική ιδέα που υπήρχε στη μέθοδο του Θαλή, γενικεύεται στο “Θεώρημα του Θαλή” ,το οποίο παραμένει, αναλλοίωτα στο χρόνο, ένα από τα πιο διάσημα θεωρήματα των Μαθηματικών.
Αναφορές
- Douglass C., Thales, California 2006.
- Guedj D., Το Θεώρημα του παπαγάλου, μετάφραση: Τεύκρος Μιχαηλίδης, Εκδόσεις ΠΟΛΙΣ, 1999.
- O’Connor J. J. and Robertson E. F., Thales of Miletus, School of Mathematics and Statistics University of St Andrews, Scotland ,1999.
- VanDerWaerdenB. L., Η αφύπνιση της επιστήμης, μετάφραση – επιμέλεια: Γιάννης Χριστιανίδης, Πανεπιστημιακές Εκδόσεις Κρήτης, 2007.
- Wikipedia, the free encyclopedia, Great pyramid of Giza.
και ένα τετράγωνο πλευράς 
, τα οποία έχουν τοποθετηθεί στο επίπεδο, κατά τέτοιον τρόπο, ώστε να έχουν μοναδικό κοινό σημείο και κάθε πλευρά του πρώτου να είναι παράλληλη προς μια πλευρά του δεύτερου. «Συμπληρώνουμε» το σχήμα, χρησιμοποιώντας κατάλληλα ορθογώνια, έτσι, ώστε, να σχηματιστεί το τετράγωνο πλευράς 
της Εικόνας 2.
,
