Τα παιχνίδια σαν το World of Warcraft δίνουν στους παίκτες τα μέσα να σώσουν κόσμους και κίνητρο να μάθουν τις συνήθειες ηρώων. Τι θα γινόταν αν μπορούσαμε να δαμάσουμε αυτήν την ισχύ των παικτών για να λύσουμε προβλήματα του πραγματικού κόσμου; Η Jane McGonigal λέει ότι μπορούμε να το κάνουμε και εξηγεί πώς στο βίντεο που ακολουθεί: Συνέχεια του άρθρου ‘Τα παιχνίδια μπορούν να κάνουν τον κόσμο μας καλύτερο.’ »
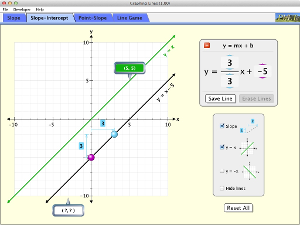
Γραφικές παραστάσεις ευθειών. Διαδραστική προσομοίωση.
Εξερευνήστε τις γραφικές παραστάσεις ευθειών και τις ιδιότητές τους.
ΜΑΘΗΣΙΑΚΟΙ ΣΤΟΧΟΙ:
Οι δραστηριότητες που περιλαμβάνονται στο λογισμικό βοηθούν τους μαθητές να:
- Εξηγούν πώς μπορεί να υπολογιστεί η κλίση της ευθείας γραμμής.
- Σχεδιάζουν τη γραφική παράσταση μιας ευθείας όταν δίνεται η εξίσωσή της.
- Βρίσκουν την εξίσωση μιας ευθείας όταν δίνεται η γραφική της παράσταση.
- Προβλέπουν πώς η αλλαγή μεταβλητών σε μια γραμμική εξίσωση θα επηρεάσει το γράφημα της .
Υποδείξεις για εκπαιδευτικούς
Το εγχειρίδιο του εκπαιδευτικού (pdf στα αγγλικά) περιέχει υποδείξεις που υποβλήθηκαν από την ομάδα του PhET.
Πηγή: phet.colorado.edu
Τράπεζα Θεμάτων Λυκείου για τις προαγωγικές εξετάσεις του Σ.Ε. 2014-15
H Τράπεζα Θεμάτων Διαβαθμισμένης Δυσκολίας (ΤΘΔΔ) περιλαμβάνει θέματα για τις προαγωγικές εξετάσεις του σχολικού έτους 2014-15 της Α΄ και Βʼ Τάξης των Γενικών Λυκείων (ΓΕΛ) και των ΕΠΑΛ, Ημερήσιων και Εσπερινών, της Α΄ και Βʼ Τάξης των Καλλιτεχνικών, Μουσικών και Εκκλησιαστικών Λυκείων, καθώς και της Βʼ και Γʼ Τάξης των Εσπερινών ΓΕΛ. Από αυτά θα κληρώνεται το 50% των θεμάτων στα εξεταζόμενα μαθήματα, όπως αυτά προσδιορίζονται στο Ν. 4186/2013 και στο Ν. 4264/2014.
Δείτε τις τα θέματα εδώ.
Εξισώσεις 1ου βαθμού. Φύλλο διδασκαλίας.
Τάξη: Β’ Γυμνασίου
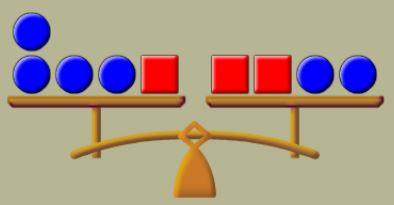
Προσδοκώμενα μαθησιακά αποτελέσματα: Να χρησιμοποιούν κάποιο μοντέλο, για παράδειγμα τη ζυγαριά ή άλλο κατάλληλο εποπτικό μέσο για να παριστάνουν και να οπτικοποιούν την έννοια της ισότητας και να ανακαλύψουν και να κατανοήσουν τις ιδιότητές της.
Να κατανοήσουν την έννοια εξίσωσης και να μάθουν τη σχετική ορολογία.
Να εφαρμόσουν τις ιδιότητες των ισοτήτων σε εξισώσεις και να συνειδητοποιήσουν ότι το να μεταφέρουμε έναν όρο από το ένα μέλος στο άλλο είναι συντόμευση των παραπάνω ιδιοτήτων. Συνέχεια του άρθρου ‘Εξισώσεις 1ου βαθμού. Φύλλο διδασκαλίας.’ »
Γιατί οι μαθητές οδηγούνται στα Φροντιστήρια. Δηλώσεις Υπουργού Παιδείας.
Αυτή τη στιγμή υπάρχουν τρεις αιτίες, που οι μαθητές οδηγούνται στα Φροντιστήρια, δήλωσε σήμερα ο υπουργός Παιδείας Α. Λοβέρδος κι εξήγησε:
Α. Η πρώτη αιτία είναι η πολλή ύλη, γι’ αυτό και τις επόμενες μέρες θα τη μειώσουμε.
Β. Το δεύτερο αίτιο είναι τα κενά, που δεν επιτρέπουν να γίνει κανονικά η διδασκαλία όλο το χρόνο.
Γ. Και το τρίτο αίτιο σε πολλές περιοχές της χώρας, είναι και μια διάθεση ανταγωνιστικότητας των γονέων. Συνέχεια του άρθρου ‘Γιατί οι μαθητές οδηγούνται στα Φροντιστήρια. Δηλώσεις Υπουργού Παιδείας.’ »
Απόψεις γονέων και εκπαιδευτικών για το «Νέο Λύκειο». Έρευνα 2014.
Βασικός σκοπός της έρευνας ήταν η αποτύπωση των απόψεων των γονέων και των εκπαιδευτικών για το «Νέο Λύκειο» καθώς και η ενημέρωση για τα βασικά σημεία του θεσμού αυτού. Επίσης διερευνήθηκαν και οι προσδοκίες των γονέων και των εκπαιδευτικών από τη Λυκειακή Εκπαίδευση των μαθητών. Η έρευνα διενεργήθηκε με την συνεργασία του εκπαιδευτικού δικτύου «Δημόσιο Σχολείο» και του εκπαιδευτικού Δημήτρη Τσιριγώτη, οποίος ήταν ο δημιουργός του ερωτηματολογίου και των γραφημάτων των αποτελεσμάτων της έρευνας καθώς και ο αναλυτής των συμπερασμάτων που εξάγονται από αυτή.
Δείτε την έρευνα εδώ
πηγή: dimosiosxoleio.com
Αριθμήσιμα και μη αριθμήσιμα απειροσύνολα.
Γνωρίζουμε ότι οι φυσικοί αριθμοί (1, 2, 3, 4, 5 …) όπως και οι άρτιοι αριθμοί (2, 4, 6,…) είναι άπειροι στο πλήθος. Με μια πρώτη ματιά νομίζει κανείς ότι οι άρτιοι αριθμοί είναι λιγότεροι από τους φυσικούς αριθμούς (δεδομένου ότι περιέχονται στο σύνολο των φυσικών αριθμών). Όμως ισχύει κάτι τέτοιο; Συνέχεια του άρθρου ‘Αριθμήσιμα και μη αριθμήσιμα απειροσύνολα.’ »
Κάθε παιδί μπορεί να τα καταφέρει στα Μαθηματικά με σκληρή δουλειά και αυτοπεποίθηση.
Δύο έμπειροι καθηγητές Μαθηματικών, ο Miles Kimball και ο Noah Smith καταρρίπτουν τον μύθο του «είμαι κακός στα Μαθηματικά» και εξηγούν γιατί κάθε παιδί μπορεί να τα καταφέρει με σκληρή δουλειά και αυτοπεποίθηση. Ένα εξαιρετικό κείμενο που πρέπει να διαβάσουν όλοι οι γονείς.
“Είμαι κακός στα Μαθηματικά”. Το ακούμε συνέχεια. Και απηυδήσαμε. Επειδή πιστεύουμε ότι η πίστη στην ιδέα των «μαθηματικών μυαλών» είναι μια από τις πιο αυτοκαταστροφικές ιδέες στις μέρες μας. Η αλήθεια είναι, ότι ενδέχεται να έχεις μαθηματικό μυαλό και πιστεύοντας το αντίθετο, απλώς περιορίζεις Συνέχεια του άρθρου ‘Κάθε παιδί μπορεί να τα καταφέρει στα Μαθηματικά με σκληρή δουλειά και αυτοπεποίθηση.’ »
Εκδόσεις για την αξιολόγηση των μαθητών στα Μαθηματικά από το ΚΕΕ.
Οι παρούσες εκδόσεις του Κέντρου Εκπαιδευτικής Έρευνας (Κ.Ε.Ε.) περιέχουν υποστηρικτικό υλικό για την αξιολόγηση των μαθητών σε μαθήματα και των τριών τάξεων του Ενιαίου Λυκείου. Εκπονήθηκε από το 1997 μέχρι το 2000 και αποτέλεσε μέρος ενός έργου που ανατέθηκε στο Κέντρο Εκπαιδευτικής Έρευνας από το ΥΠ. Ε. Π. Θ., με γενικό τίτλο «Ανάπτυξη και διάδοση νέων μεθόδων αξιολόγησης στο Λύκειο». Συνέχεια του άρθρου ‘Εκδόσεις για την αξιολόγηση των μαθητών στα Μαθηματικά από το ΚΕΕ.’ »
Περιοδικά Ευκλείδης Α΄ και Ευκλείδης Β΄ 2014 σε μορφή pdf
ΕΥΚΛΕΙΔΗΣ Α και ΕΥΚΛΕΙΔΗΣ Β 2013-2014
ΨΗΦΙΑΚΗ ΕΚΔΟΣΗ ΕΥΚΛΕΙΔΗ Α’ ΚΑΙ ΕΥΚΛΕΙΔΗ Β’ 2013-2014
(ΤΕΥΧΗ 89, 90, 91, 92)
ΧΟΡΗΓΟΣ ΕΚΔΟΣΗΣ ΚΟΙΝΟΦΕΛΕΣ ΙΔΡΥΜΑ
ΙΩΑΝΝΗ Σ. ΛΑΤΣΗ Συνέχεια του άρθρου ‘Περιοδικά Ευκλείδης Α΄ και Ευκλείδης Β΄ 2014 σε μορφή pdf’ »