Αρχική » Γρίφοι (Σελίδα 2)
Αρχείο κατηγορίας Γρίφοι
Γρίφος Νο 38 – Αλήθεια, Ψέματα
O Γιάννης λέει την αλήθεια την Δευτερα,Τριτη,Τεταρτη και Πεμπτη.
Τις άλλες μέρες λέει ψέματα.
Η Μαρία λεει την αλήθεια την Παρασκευη, Σαββατο ,Κυριακη και Δευτέρα.
Τις αλλες μερες λέει ψεματα.
Κάποια μέρα την προηγούμενη εβδομάδα και οι δυο είπαν το ακόλουθο
”Είπα ψέματα χθες”.
Ποια μέρα της εβδομάδας ήταν αυτή ;
ΠΗΓΗ : Κωνσταντίνος Μιχαηλίδης , ανάρτηση στο fb 18.01.18 και ώρα 17:05.
Γρίφος Νο 37 – Η ηλικία της γιαγιάς
Γρίφος αναρτημένος στο ιστολόγιο του συνάδερφου Δ. Χονδρολίδη.
Μπορείτε να τον δείτε ΕΔΩ : http://dimitris-ver.blogspot.gr/2018/01/blog-post_10.html
Προσπελάστηκε 12.01.18 και ώρα 16:50.
Γρίφος Νο 36 Βαρέλια Πετρελαίου
“Η ημερήσια παραγωγή 20 πηγαδιών άντλησης πετρελαίου είναι 4000 βαρέλια.
Για κάθε νέο πηγάδι που ανοίγεται , η ημερήσια παραγωγή κάθε πηγαδιού μειώνεται κατά 5 βαρέλια. Να βρεθεί ο αριθμός των νέων πηγαδιών , ώστε να έχουμε μέγιστη ημερήσια παραγωγή.”
Εναλλακτικά , μπορείτε να απαντήσετε στα παρακάτω ερωτήματα :
α ) Να εκφραστεί η ολική παραγωγή βαρελιών , ως συνάρτηση του αριθμού x των νέων πηγαδιών.
β ) Για ποια τιμή του x έχουμε μέγιστη ημερήσια παραγωγή βαρελιών ; Αιτιολογήστε.
ΠΗΓΗ : Ανάλυση Γ΄ Λυκείου , ΟΕΔΒ , Έκδοση 1993 , σελίδα 38.
Γρίφος Νο 35 – Το συνεπές Τρένο
Μια αμαξοστοιχία που κινείται με μέση ταχύτητα 72 km/h , πρέπει να διανύσει μια απόσταση σε 9 ώρες ακριβώς.
Μετά απο ταξίδι 144 km υποχρεώνεται να σταματήσει για τα 3/4 της ώρας.
Να βρεθεί με ποια ταχύτητα πρέπει να συνεχίσει το ταξίδι ,μετά τη διακοπή, για να φτάσει στο προορισμό της στην ώρα της.
ΠΗΓΗ : Μαθηματικά Α΄ Γυμνασίου , ΟΕΔΒ , Αθήνα , Έκδοση 2006.
Γρίφος Νο 34 Η κληρονομιά
“Ένας πατέρας στη διαθήκη του αφήνει το 1/3 της περιουσίας του στην ετοιμόγενη γυναίκα του και τα 2/3 στον γιο του, αν γεννήσει η γυναίκα του γιο. Αν γεννήσει κόρη , τότε αφήνει στη γυναίκα του τα 2/3 της περιουσίας και το 1/3 στη μέλλουσα κόρη του.
Πεθαίνει ο πατέρας και η γυναίκα του γεννά δίδυμα ένα αγόρι και ένα κορίτσι.
Πώς πρέπει να μοιραστεί η περιουσία ;”
ΠΗΓΗ : Παιδαγωγικό Τμήμα Δημοτικής Εκπαίδευσης , Ρόδος , 2017.
Γρίφος Νο 33 “Ξεχασιάρης!”
Καθώς ο Ιορδάνης πηγαίνει στο σχολείο θυμήθηκε ότι ξέχασε τον διαβήτη του ! Υπολόγισε ότι αν συνεχίσει για το σχολείο θα φτάσει 11 λεπτά πριν το κουδούνι, ενώ αν γυρίσει σπίτι να πάρει τον διαβήτη θα φτάσει στο σχολείο με καθυστέρηση 7 λεπτών. Με δεδομένο ότι οι διαδρομές του θα γίνουν με τον ίδιο ρυθμό βαδίσματος , υπολογίστε πόσα λεπτά απέχει το σπίτι του Ιορδάνη από το σημείο που θυμήθηκε τον διαβήτη.
ΠΗΓΗ : Οδός Μαθηματικής Σκέψης, Γ. Θωμαϊδης – Γ. Ρίζος , Εκδόσεις Μαυρίδη , Θεσ/νίκη 2017.
Γρίφος Νο 32 “Ο Αλκοολικός Υπάλληλος”
“Από το γεμάτο με Βότκα μπουκαλάκι του αφεντικού του , ο Νίκος πίνει μια μέρα ένα σφηνάκι. Για να μην γίνει αντιληπτός , γεμίζει το μπουκάλι με νερό (αντικαθιστά το σφηνάκι που ήπιε με νερό). Την επόμενη μέρα πίνει ένα διπλό σφηνάκι και ξαναγεμίζει με νερό. Νερομένη όπως είναι η Βότκα, την επόμενη ο Νίκος χρειάζεται 3 σφηνάκια. Τα πίνει και …….ξαναγεμίζει με νερό. Επαναλαμβάνεται η ίδια διαδικασία , αυξάνοντας τα σφηνάκια κάθε μέρα κατά ένα. Την 16η μέρα πίνει όλο το μπουκάλι. “
Πόσο νερό ήπιε συνολικά ο Νίκος ;
ΠΗΓΗ : Οδός Μαθηματικής Σκέψης , Γ. Θωμαϊδης – Γ. Ρίζος , Εκδόσεις Μαυρίδη , Θεσ/νίκη 2017.
Γρίφος Νο 31 – Ο Έμπειρος Ταξιτζής
Είμαστε στην πόλη Α. Παίρνουμε ένα ταξί για την πόλη Β. Αμέσως μόλις ξεκινάμε , ρωτάμε τον ταξιτζή : “Σε πόση ώρα θα φτάσουμε στη πόλη Β; ”
Μας απαντάει : “Αν έχει κίνηση ο δρόμος και πηγαίνουμε με 60 χλμ/ώρα , θα φτάσουμε στις 12:00 μ.μ. Αν όχι και πηγαίνουμε με 100 χλμ/ώρα θα φτάσουμε στις 10:00 π.μ. Αν η κίνηση είναι μέτρια και πάμε με 75 χλμ/ώρα θα φτάσουμε στις 11:00 π.μ .”
“Συγνώμη , εννοείτε 80 χλμ/ώρα που είναι ο μέσος όρος των 60 και 100 αντίστοιχα.”
“Όχι , όχι ” , μας απαντά ο ταξιτζής , “την έχω κάνει πολλές φορές τη διαδρομή. Με 75 χλμ/ώρα θα φτάσουμε ακριβώς στις 11:00 π.μ , όπως σας είπα.”
α ) Τι ώρα γίνεται η παραπάνω κουβέντα ;
β ) Ποια η απόσταση των πόλεων Α και Β ;
γ ) Για να επιμένει ο ταξιτζής , μάλλον έχει δίκιο , εσείς τι λέτε ; Αιτιολογήστε.
ΠΗΓΗ : Οδός Μαθηματικής Σκέψης, Γ. Θωμαΐδης – Γ. Ρίζος , Εκδόσεις Μαυρίδη , Θεσ/νίκη 2017 , σελίδα 81.
Γρίφος Νο 29 – Μέση Ταχύτητα (Αρμονικός Μέσος)
“Ένα παλιό αυτοκίνητο πρόκειται να διανύσει μια απόσταση ενός χιλιομέτρου προς την κορυφή ενός λόφου και να επιστρέψει. Λόγω παλαιότητας δεν μπορεί να διανύσει το πρώτο χιλιόμετρο – την άνοδο – γρηγορότερα από μια μέση ταχύτητα 15 χλμ / ώρα.
Με ποια ταχύτητα πρέπει να καλύψει το δεύτερο χιλιόμετρο – στην κάθοδο μπορεί να πάει βέβαια γρηγορότερα – ώστε να επιτύχει μέση ταχύτητα (για τη συνολική απόσταση ) 30 χλμ / ώρα ; “ (περισσότερα…)
Γρίφοι Νο 27-28
Αν και τα παρακάτω προβληματάκια συγκαταλέγονται λιγότερο στους γρίφους και περισσότερο στην Πρακτική Αριθμητική, αξίζει να μελετηθούν. (περισσότερα…)
Γρίφος Νο 26 Άθροισμα χωρίς Κόπο
Μπορείτε να υπολογίσετε το άθροισμα όσο πιο γρήγορα γίνεται , χωρίς αριθμομηχανή και χωρίς μολύβι και χαρτί ; Πείτε μου τον τρόπο σκέψης σας.
154+308+616+308+154 = ?
ΠΗΓΗ : Ευκλείδης Α΄ τ.103
Γρίφος Νο 25 – Αποτέλεσμα 21
Χρησιμοποιώντας τους αριθμούς 1,2,3,7 απο μια φορά τον καθένα και κάνοντας χρήση των πράξεων + , – , x , : , όσες φορές θέλετε , μπορείτε να βγάλετε αποτέλεσμα 21 ;
ΠΗΓΗ : Ευκλείδης Β΄ τ.100
Γρίφος Νο 24 – Δεύτερη Ακολουθία
Ποιοι αριθμοί ακολουθούν στην παρακάτω ακολουθία και γιατί ;
1, 2 , 3 , 4 , 5 , 8 , 7 , 16 , 9 , ……… , ………..
ΠΗΓΗ : Ευκλείδης Α΄ τ.102
Γρίφος Νο 23 – Σκέψου δυο μονοψήφιους
“Σκέψου δυο μονοψήφιους αριθμούς, πενταπλασίασε τον πρώτο και στο γινόμενο πρόσθεσε 4. Τον αριθμό που βρήκες πολλαπλασίασε τον με το 2 και πρόσθεσε τον δεύτερο αριθμό . Αφαίρεσε από το αποτέλεσμα το 8. Τα ψηφία του αριθμού που βρήκες είναι οι αριθμοί που σκέφτηκες αρχικά !”
Μπορείς να εξηγήσεις αναλυτικά τον παραπάνω γρίφο ;
ΠΗΓΗ : Ευκλείδης Α΄ τεύχος 101.
Γρίφος Νο21 – Η Χρύσα και το τρένο
Η Χρύσα θέλει να πάρει το τρένο που φεύγει στις 10:45π.μ και θα πάει στο σταθμό του τρένου με το ποδήλατο της ο οποίος βρίσκεται σε απόσταση 6 χλμ απ το σπίτι της.
Τα πρώτα 2 χλμ είναι σε ανηφόρα , τα επόμενα 2 σε επίπεδο και τα τελευταία 2 χλμ σε κατηφόρα.
Η Χρύσα μπορεί να οδηγήσει το ποδήλατο με 2χλμ/ώρα στην ανηφόρα , με 3χλμ/ώρα στο επίπεδο και με 4χλμ/ώρα στη κατηφόρα.
Υποθέτει οτι θα έχει μέση ταχύτητα 3 χλμ/ώρα, για αυτό σκοπεύει να φύγει απ το σπίτι της 8:40π.μ
Πιστεύει οτι θα τις περισσέψουν και 5 λεπτά να κλειδώσει το ποδήλατο της και να επιβιβαστεί στο τρένο. Θα προλάβει η Χρύσα το τρένο ;
ΠΗΓΗ : Ευκλείδης Α΄ τ.89
Γρίφος Νο 20 – Το σκάψιμο της τρύπας
Αν για να σκαφτεί μια τρύπα 3μέτρα μήκος, 3 μέτρα πλάτος και 3 μέτρα βάθος απο 2 εργάτες , χρειάζονται 2 ώρες,
πόσες ώρες χρειάζονται οι 2 αυτοί εργάτες για να σκάψουν μια τρύπα
6μέτρα μήκος, 6 μέτρα πλάτος και 6 μέτρα βάθος, θεωρώντας οτι δουλεύουν με τον ίδιο ρυθμό ;
ΠΗΓΗ : Ευκλείδης Α΄ τ.89
Γρίφος Νο 19 – Ο διαβάτης και η Τελειότητα !
Κάποιος διαβάτης φτάνει σε ένα σταυροδρόμι.
Έχει να επιλέξει ανάμεσα σε 3 μονοπάτια.
Θέλει να βαδίσει αυτό που οδηγεί στην τελειότητα και ξέρει καλά οτι μόνο ένα απο το τρια οδηγεί σε αυτή.
Το μονοπάτι προς τα δεξιά έχει πινακίδα που γράφει :
<< Αυτό το μονοπάτι οδηγεί στην τελειότητα>>.
Το μονοπάτι προς τα εμπρός έχει πινακίδα που γράφει :
<<Αυτό το μονοπάτι δεν οδηγεί στην τελειότητα >>.
Το μονοπάτι απ τα αριστερά έχει πινακίδα που γράφει :
<<Το μονοπάτι προς τα εμπρός δεν οδηγεί στην τελειότητα>>.
Άν τουλάχιστον μια πινακίδα λέει την αλήθεια και τουλάχιστον μία πινακίδα λέει ψέματα, ποιο μονοπάτι πρέπει να ακολουθήσει ο διαβάτης για να οδηγηθεί στην τελειότητα ;
Γρίφος Νο 18 – Διψήφιοι Πρώτοι
Βρείτε το άθροισμα του μικρότερου πρώτου διψήφιου και του μεγαλύτερου πρώτου διψήφιου αριθμού , των οποίων τα ψηφία είναι επίσης πρώτοι αριθμοί.
Παράκληση : Οι απαντήσεις σας να συνοδεύονται απο όνομα και επώνυμο , ανώνυμα δεν δημοσιεύονται.
ΠΗΓΗ : Ευκλείδης Α΄ τ.86
Γρίφος Νο 17 – Ο εξαψήφιος αριθμός
Βρείτε έναν εξαψήφιο αριθμό του οποίου το πρώτο ψηφίο είναι μια μονάδα μεγαλύτερο απ το τρίτο , το δεύτερο είναι μια μονάδα μικρότερο απ το τέταρτο, το πέμπτο είναι μια μονάδα μικρότερο απ το τρίτο και το έκτο ψηφίο είναι μια μονάδα μεγαλύτερο απ το τέταρτο.
Το άθροισμα του δεύτερου και τρίτου ψηφίου ισούται με το πρώτο , ενώ το άθροισμα όλων των ψηφίων είναι 30.
Παράκληση : Οι απαντήσεις σας να συνοδεύονται απο όνομα και επώνυμο , ανώνυμα δεν δημοσιεύονται.
ΠΗΓΗ : Ευκλείδης Α΄ , τ.86
Γρίφος Νο 16 – Συμπλήρωσε τις ισότητες
Στις παρακάτω τρεις ισότητες, μπορείτε να βρείτε τους αριθμούς που λείπουν, αν ξέρετε πως ο καθένας απ αυτούς είναι μονοψήφιος και πως το κάθε ψηφίο απο το 1 μέχρι το 9 μπορεί να χρησιμοποιηθεί μία μόνο φορά ;
(……. x ……..) – …………. = 0
(……. – ……..) + …………= 10
(……. x …….) – ………… =20
ΠΗΓΗ : τ 46 Ευκλείδης Α’
Γρίφος Νο 15 – Διαγωνισμός Μαθηματικών (Κατάταξη)
Η Αλίκη , η Βασιλική , ο Κώστας , η Ελένη , ο Γιώργος και η Κατερίνα συμμετείχαν σε ένα διαγωνισμό μαθηματικών.
Απο τα αποτελέσματα του διαγωνισμού έχουμε τα ακόλουθα :
α ) Η Ελένη ήταν μια θέση πάνω απο την Αλίκη.
β ) Η Βασιλική δεν ήταν ούτε πρώτη ούτε τελευταία.
γ ) Ο Γιώργος ήταν δυο θέσεις πάνω απ τον Κώστα.
δ ) Η Κατερίνα κατατάχθηκε σε άρτια θέση.
ε ) Η Αλίκη κατατάχθηκε σε περιττή θέση.
Βρείτε την κατάταξη τους :
1. …………………………
2. …………………………
3. …………………………
4. ………………………..
5. ………………………
6. ………………………
ΠΗΓΗ : ΕΥΚΛΕΙΔΗΣ Α’ τ.84
Γρίφος Νο 13 – Αγώνας Ταχύτητας 100 μέτρων ή 110 μέτρων !
Ο Θανάσης και ο Διονύσης έτρεξαν σε μια κούρσα 100 μέτρων.
Όταν ο Θανάσης τερμάτισε , ο Διονύσης βρισκόταν στα 90 μέτρα.
Πρότεινε λοιπόν ο Θανάσης στο Διονύση να ξανατρέξουν άλλα αυτή τη φορά θα ξεκινούσε ο Θανάσης 10 μέτρα πίσω απ το Διονύση. Αν κρατηθούν όλες οι συνθήκες ίδιες , ποιος θα κερδίσει και γιατί ;
ΠΗΓΗ : ΕΥΚΛΕΙΔΗΣ Α’ τ. 82
Γρίφος Νο 12 – Η ακολουθία
Παρατηρήστε την ακολουθία :
1 , 11 , 21 , 1211 , 111221 , 312211 , 13112221 , ……………………………………
Οι όροι της προκύπτουν απο τον ή τους προηγούμενους όρους , όχι όμως μετά απο κάποιες αριθμητικές πράξεις .
Ποιός είναι ο επόμενος αριθμός που λείπει ;
ΠΗΓΗ ΓΡΙΦΟΥ : ΕΥΚΛΕΙΔΗΣ Α’ τ.63
Γρίφος Νο 11 – Το φιλοδώρημα που μπερδεύει ακόμη και σήμερα!
Τρεις φίλοι πάνε να φάνε σε ένα εστιατόριο.Έρχεται ο λογαριασμός 30€. Δίνει λοιπόν ο καθένας απο 10€. (περισσότερα…)
Γρίφος Νο 10 – Η σύνταξη
Ένας επιχειρηματίας σκέφτηκε το παρακάτω συνταξιοδοτικό πρόγραμμα για τους υπαλλήλους του: Τους είπε πως θα τους δώσει σύνταξη αμέσως μόλις ο καθένας τους εργασθεί για 8 καθαρές ώρες στο ταμείο της εταιρίας. (περισσότερα…)
Γρίφος Νο9 – Τα πρόβατα (Κληρονομιά)
Ο καπετάν Γιάννης αισθάνεται το τέλος του.
Έχει 3 γιους στους οποίους θέλει και να μοιράσει, όπως αυτός πιστεύει δίκαια, την περιούσια του.
Η περιούσια του είναι μόνο 19 πρόβατα. Ούτε 18 ούτε 20, 19.
Στον πρώτο του γιο ως και πρωτότοκος θέλει να αφήσει το 1/2 των πρόβατων. Στον δεύτερο το 1/4 των πρόβατων. και στο τρίτο και τελευταίο το 1/5.
Σε καμία περίπτωση δεν θέλει οι γιοι του να χωρίσουν τα πρόβατα σε κομμάτια, σκοτώνοντας τα. Βλέπεις αγαπάει τα πρόβατα σαν παιδία του.
Τι πρέπει να κάνουν οι γιοι του ;
Ευχαριστώ το συντάκτη του γρίφου Μαρία Στόικου (μαθήτρια της Α΄Γυμνασίου- 2011) για την αποστολή.
Γρίφος Νο 8 – Το κουδούνι
Μόλις έχω μετακομίσει σε διαμέρισμα του 5ου ορόφου πολυκατοικίας,
η οποία έχει 7 ορόφους και κάθε όροφος 3 διαμερίσματα.
Τα κουδούνια στην είσοδο της πολυκατοικίας είναι ανακατεμένα
και εγώ δεν ξέρω ποιο αντιστοιχεί στο δικό μου θυροτηλέφωνο.
Είμαι μόνος μου και έχω στη διάθεσή μου μόνο ένα κασετόφωνο
και μια άγραφη κασέτα.
Πως μπορώ να εντοπίσω το κουδούνι που αντιστοιχεί στο διαμέρισμά μου;
ΣΥΝΤΑΚΤΗΣ ΓΡΙΦΟΥ : ΚΙΚΗ ΠΑΠΑΔΟΠΟΥΛΟΥ πρώην ΜΑΘΗΤΡΙΑ ΓΥΜΝΑΣΙΟΥ ΕΞΑΠΛΑΤΑΝΟΥ




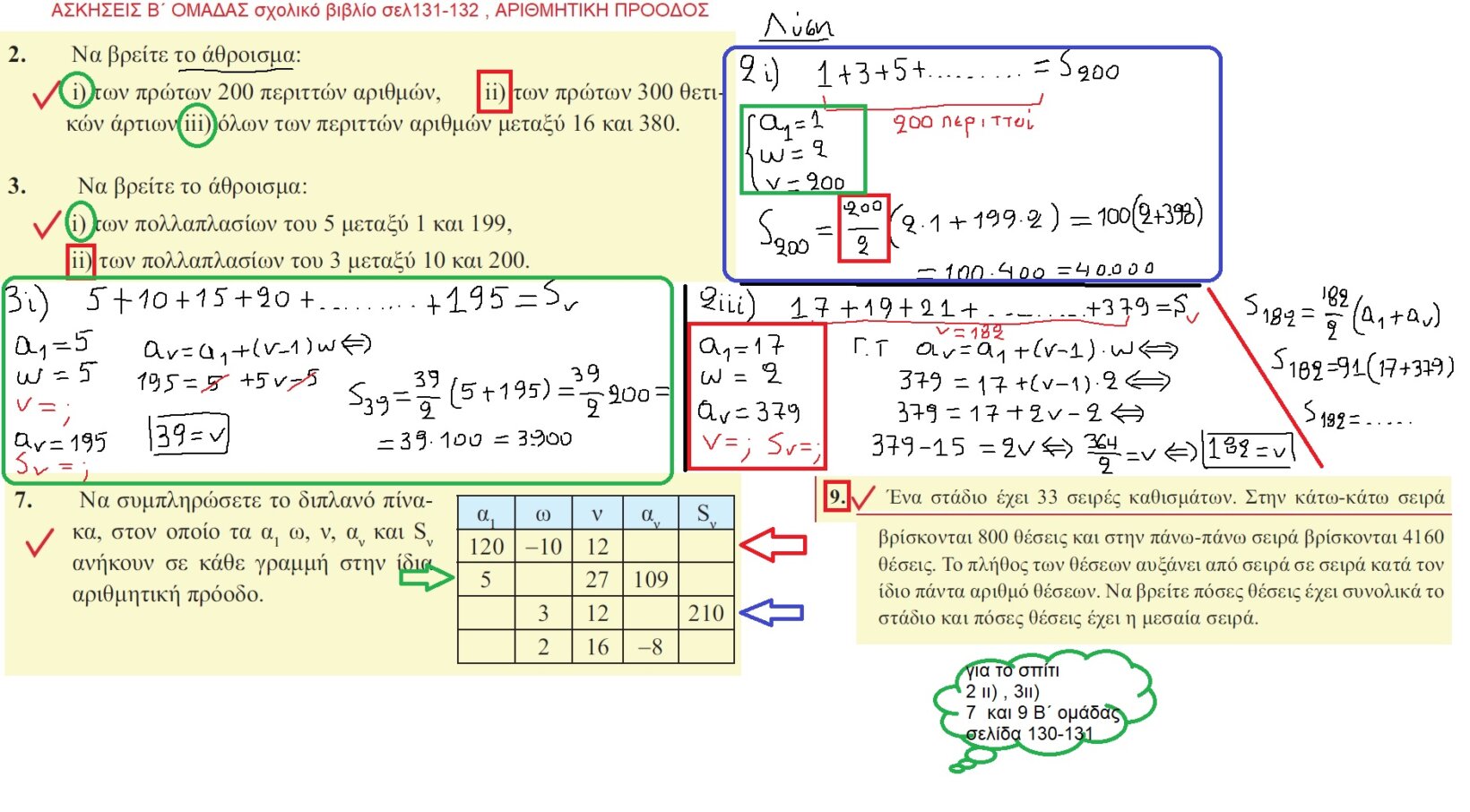
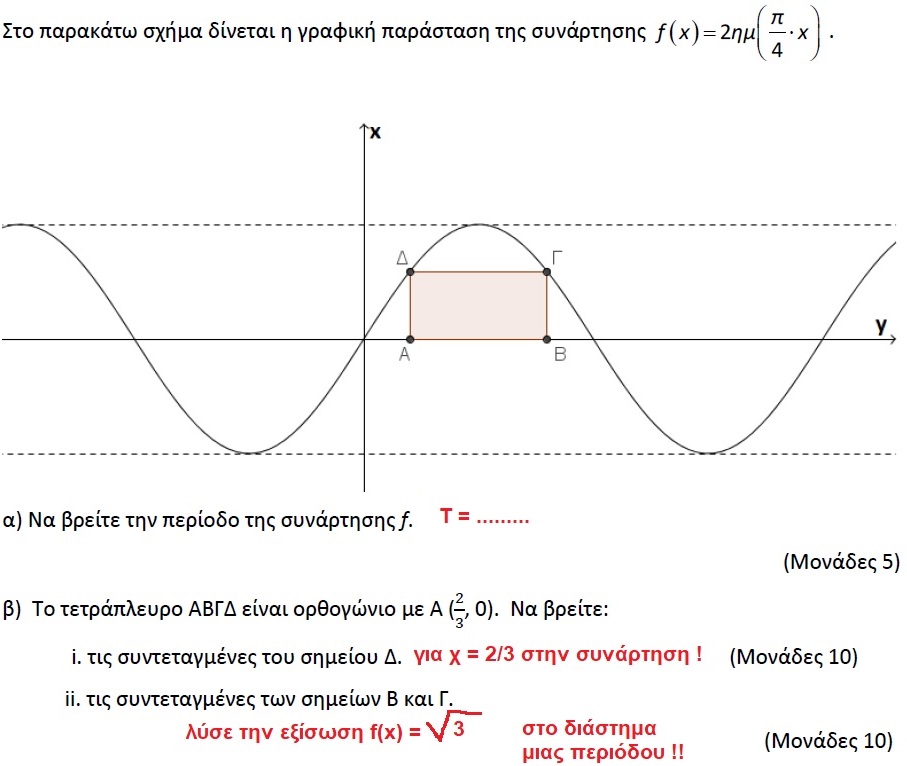

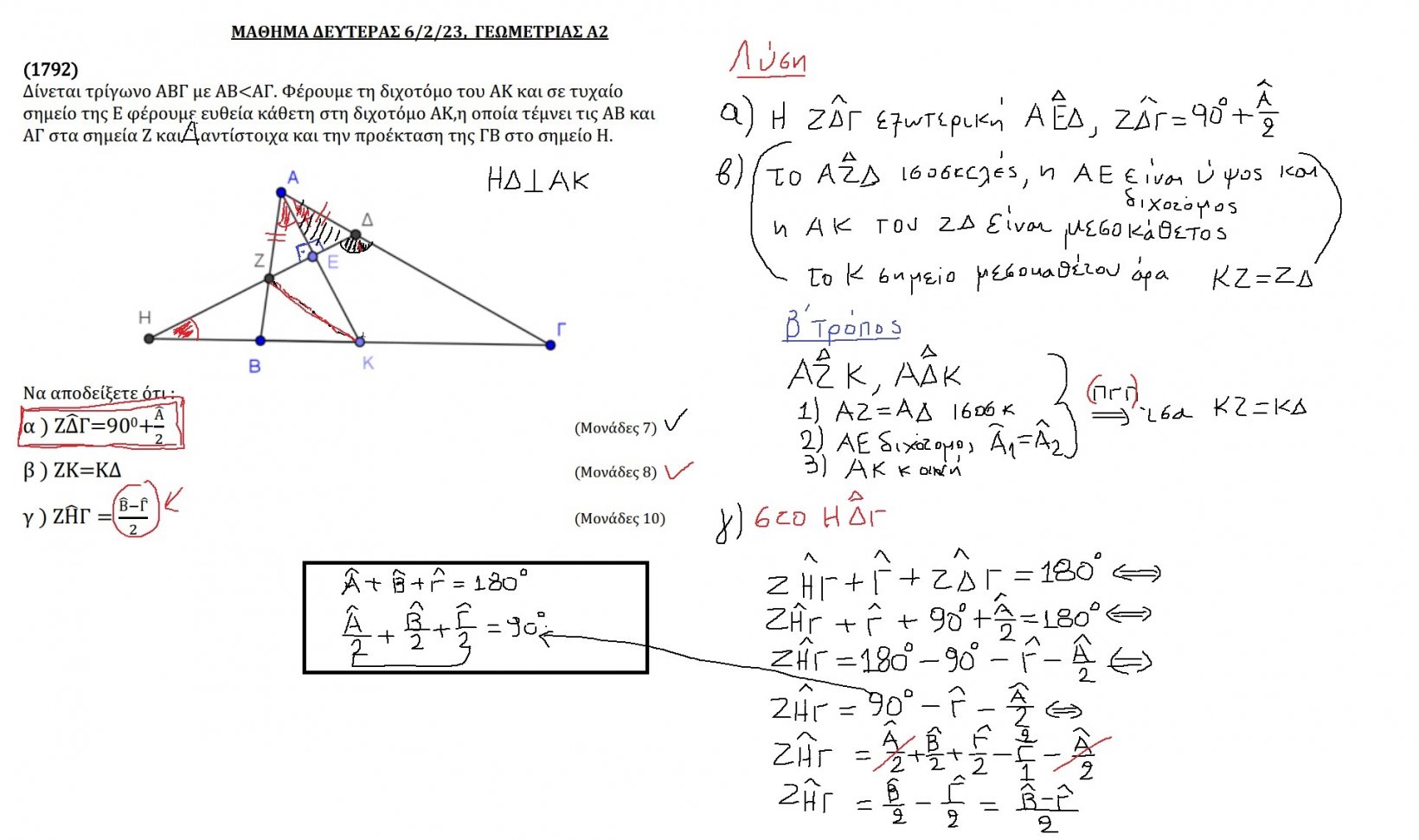





























 E-DASKALOS
E-DASKALOS e-sos
e-sos Geogebra Math Apps
Geogebra Math Apps LISARI
LISARI MATH A MAGIC PATH
MATH A MAGIC PATH MATHEMATICA
MATHEMATICA MATHMAGIC
MATHMAGIC Αρωγή Παιδείας
Αρωγή Παιδείας Άσκηση
Άσκηση Ασκησόπολις
Ασκησόπολις ΓΕ.Λ ΑΡΙΔΑΙΑΣ
ΓΕ.Λ ΑΡΙΔΑΙΑΣ ΔΔΕ Πέλλας
ΔΔΕ Πέλλας Ε.Μ.Ε
Ε.Μ.Ε Ε.Μ.Ε -Κεντρικής Μακεδονίας
Ε.Μ.Ε -Κεντρικής Μακεδονίας ΕΚΔΟΣΕΙΣ
ΕΚΔΟΣΕΙΣ ΜΑΘ&ΛΟΓΟΤΕΧΝΙΑ
ΜΑΘ&ΛΟΓΟΤΕΧΝΙΑ Ο Άγνωστος Χ
Ο Άγνωστος Χ Ο Μαθηματικός
Ο Μαθηματικός Υπουργείο Παιδείας
Υπουργείο Παιδείας
































































Πρόσφατα σχόλια