1) ΚΑΤΑΣΚΕΥΗ ΤΡΙΓΩΝΟΥ ΑΒΓ
Δίνονται τρεις αριθμοί α, β, γ. Μπορούμε πάντα να κατασκευάζουμε τρίγωνο με πλευρές τα μήκη α, β, γ;
Ποια σχέση πρέπει να συνδέει τα α, β, γ ώστε να κατασκευάζεται τρίγωνο;
Εναλλακτικά το αρχείο ΕΔΩ
ααα
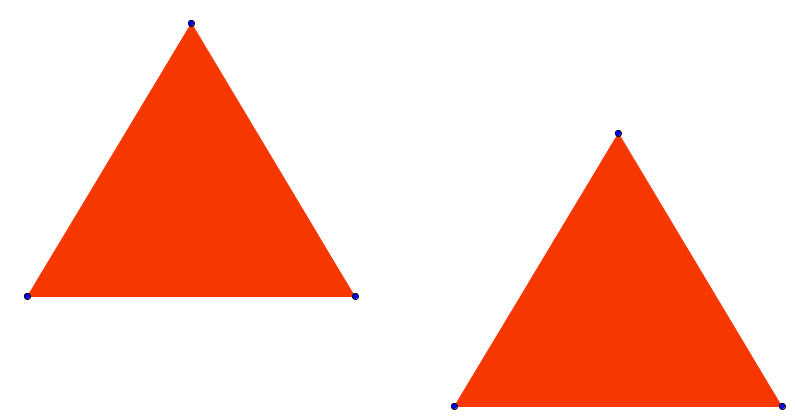
- Το παραπάνω τρίγωνο που βλέπετε έχει κατασκευαστεί με μήκη πλευρών 9.4εκ, 8.3εκ, 6.6εκ.
Μπορείτε να κατασκευάσετε τρίγωνο με μήκη πλευρών του 4εκ, 6εκ, 15εκ; Ναι ή όχι και γιατί;
ααα
2) ΥΨΗ ΤΡΙΓΩΝΟΥ ΑΒΓ
Πόσα ύψη έχει ένα τρίγωνο; Που τέμνονται; Από τι εξαρτάται η θέση του σημείου τομής τους;
Ασχοληθήτε με τη δραστηριότητα που προτείνεται.
(Πατήστε πάνω στην εικόνα τριγώνων)
Εναλλακτικά το αρχείο ΕΔΩ
ααα
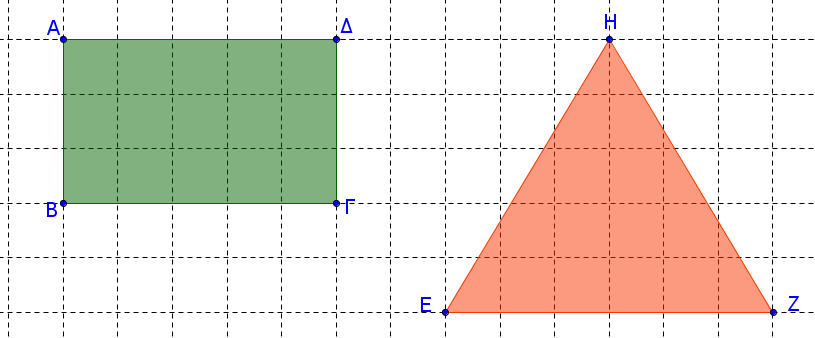
3) ΤΥΠΟΣ ΕΜΒΑΔΟΥ ΤΡΙΓΩΝΟΥ ΑΒΓ
Να βρείτε τον τύπο εμβαδού τριγώνου, όταν είναι γνωστός ο τύπος εμβαδού παραλληλογράμμου.
(Πατήστε πάνω στην εικόνα που ακολουθεί)

Εναλλακτικά το αρχείο ΕΔΩ
ααα
- Να αποδείξετε ότι ο τύπος του εμβαδού τριγώνου ΑΒΓ είναι:
(ΑΒΓ) = (α .υα)/2= (β . υβ)/2 =(γ . υγ) /2
οπου α, β, γ είναι οι πλευρές του τριγώνου και υα, υβ, υγ είναι τα αντίστοιχα ύψη.
ααα
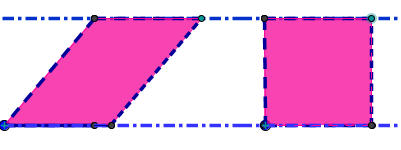
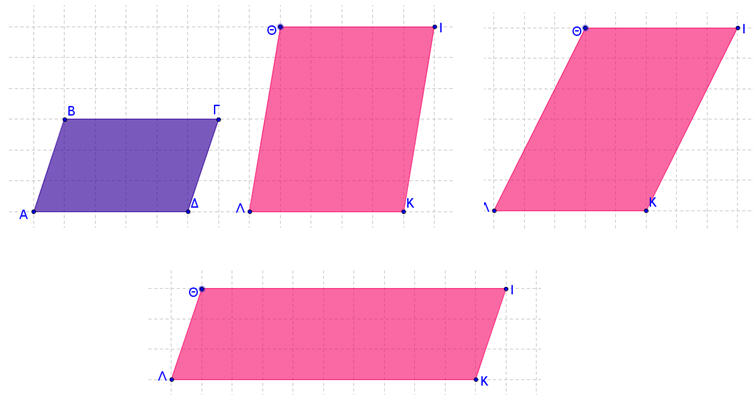
4) ΙΣΟΔΥΝΑΜΑ ΤΡΙΓΩΝΑ
Να βρείτε τη σχέση των εμβαδών τριγώνων με ίδια/ίση βάση και ίδιο/ίσο, το αντίστοιχο ύψος.
(Πατήστε πάνω στην εικόνα που ακολουθεί)

Εναλλακτικά το αρχείο ΕΔΩ
ααα
- Τα τρίγωνα του παρακάτω σχήματος είναι ισοδύναμα; Γιατί;