popiardv's blog

Ο Ερατοσθένης γεννήθηκε στην Κυρήνη, στη σημερινή Λιβύη, έζησε, εργάστηκε και πέθανε στην Αλεξάνδρεια, πρωτεύουσα της Αιγύπτου. Σπούδασε στην Αλεξάνδρεια και ισχυριζόταν ότι επίσης σπούδασε για κάποια χρόνια στην Αθήνα. Το 236 π.Χ. ορίστηκε από τον Πτολεμαίο τον Γ΄ τον Ευεργέτη βιβλιοθηκάριος της βιβλιοθήκης της Αλεξάνδρειας, διαδεχόμενος τον Ζηνόδοτο. Δεν παντρεύτηκε ποτέ. Το 194 π.Χ. τυφλώθηκε και ένα χρόνο αργότερα σταμάτησε να τρώει και πέθανε.

Ήταν ο πρώτος που υποστήριξε ότι η Γη είναι μια σφαίρα που βρίσκεται στο κέντρο του σύμπαντος, το οποίο περιστρέφεται με συχνότητα εικοσιτεσσάρων ωρών. Επινόησε επίσης το σύστημα των γεωγραφικών παραλλήλων. Διατύπωσε δε την υπόθεση, ότι είναι δυνατόν να ταξιδέψουμε κατά μήκος μιας γεωγραφικής παράλληλου ξεκινώντας από την Ιβηρία και να φτάσουμε έως την Ινδία, διαπλέοντας τον Ατλαντικό ωκεανό. Ο Στράβων που διέσωσε και μας μετέφερε την θεωρία αυτή, προσέθεσε μάλιστα, ότι στο ταξίδι αυτό ίσως να συναντούσαμε νέα άγνωστα μέρη ξηράς.

Ένα από τα πιο σημαντικά πειράματα που πραγματοποιήθηκε στην ιστορία της ανθρωπότητας ήταν η μέτρηση της περιφέρειας της γης από τον Ερατοσθένη τον 3 π.Χ. αιώνα. Ο Ερατοσθένης πληροφορήθηκε ότι στη Συήνη (σημερινό Ασουάν) ο ήλιος κατά το μεσημέρι του θερινού ηλιοστασίου ρίχνει τις ακτίνες του κάθετα στον ορίζοντα και φωτίζει τον πυθμένα ενός πηγαδιού. Την ίδια στιγμή στην Αλεξάνδρεια οι ακτίνες του ηλίου σχηματίζουν μια γωνία 7^ο με την κατακόρυφο του τόπου. Στη συνέχεια μέτρησε την απόσταση Αλεξάνδρειας – Συήνης και υπολόγισε, όπως φαίνεται στο σχήμα που ακολουθεί, με αξιοζήλευτη ακρίβεια την περιφέρεια της γης.

Στις 21 Μαρτίου 2014 γύρω στις 12 το μεσημέρι πολλά σχολεία στον κόσμο θα επαναλάβουν το πείραμα του Ερατοσθένη.  Οι μαθητές θα μετρήσουν τη σκιά μιας ράβδου μήκους ενός μέτρου,  η οποία θα είναι κάθετη στο επίπεδο της γης (τοπικά). Οι ακτίνες του ήλιου είναι πάντα παράλληλες μεταξύ τους αλλά οι ράβδοι θα σχηματίζουν διαφορετικό μήκος σκιάς ανάλογα με το πόσο βορειότερα από τον Ισημερινό βρίσκεται ή όχι το μέρος που θα λάβει μέρος το πείραμα.

Οι μαθητές μας της Α΄ και της Γ΄ τάξης θα βρίσκονται στον τόπο του πειράματος 10 λεπτά νωρίτερα για να παίρνουν συνεχώς μετρήσεις και να τις σημειώνουν στο σημειωματάριο τους. Μόλις η σκιά της ράβδου πάρει την μικρότερη τιμή θα σημειώσουν το μήκος της σκιάς της ράβδου και οι μαθητές της Α΄ τάξης θα μετρήσουν τη γωνία που σχηματίζουν οι ακτίνες του ήλιου με τη ράβδο ενώ της Γ΄ τάξης θα την υπολογίσουν με τη βοήθεια των τριγωνομετρικών αριθμών.

Τα υλικά που θα διατίθενται για τις παραπάνω μετρήσεις είναι ράβδος του ενός μέτρου , άσπρη κόλλα χαρτί,  μετροταινία, γνώμονας, μοιρογνωμόνιο, χάρακας.

Στη συνέχεια, μια επόμενη μέρα το σχολείο μας θα βρει άλλο σχολείο στον ίδιο μεσημβρινό για να βρούμε την απόσταση των δύο σχολείων (μήκος τόξου) και από τις δικές τους μετρήσεις να υπολογίσουμε το μέτρο του τόξου (επίκεντρη γωνία) και με αυτές τις δύο πληροφορίες μέτρο και μήκος τόξου να υπολογίσουμε την περιφέρεια της γης.

Δείτε το σχετικό αρχείο Geogebra της συναδέλφου Ειρήνης Περυσινάκη ΕΔΩ

Το γεωγραφικό μήκος και πλάτος του σχολείου μας και η ώρα που μεσουρανεί ο ήλιος στις 21 Μαρτίου από το  http://www.esrl.noaa.gov/gmd/grad/solcalc/ φαίνεται στη παρακάτω εικόνα: 

Δοκιμαστικές μετρήσεις στην αυλή μας

Σήμερα 20 Μαρτίου  κάναμε δοκιμαστικές μετρήσεις από τις 12.15 με το τμήμα Α1 και τις ολοκληρώσαμε με το Γ2 μέχρι τις 12.45.  Στρώσαμε μία κόλλα χαρτί σε οριζόντιο έδαφος και πάνω τοποθετήσαμε μία ράβδο ώστε να είναι κάθετη με το έδαφος. Προσπαθήσαμε να στηρίξουμε όσο καλύτερα γινόταν τη ράβδο γιατί φυσούσε κάθε τόσο και είτε φούσκωνε το χαρτί, είτε κινείτο η ράβδος οι μετρήσεις μας άλλαζαν μέχρι και 2 εκατοστά.   Αύριο θα φροντίσουμε να στηρίξουμε καλύτερα τις ράβδους για την τελική μέτρηση. 

Παράλληλα από το πρωί βάλαμε σημάδια στην αυλή μας, που αφορούσαν τη σκιά ενός πασσάλου του βόλεϊ. Οι μαθητές παρατηρούσαν έκπληκτοι όλη την ημέρα την μείωση της σκιάς του αλλά και τη στροφή της συνεχώς. Κάποια στιγμή δοκίμασαν να βρουν πόσο έστριψε ο ήλιος σε σχέση με την πρώτη πρωινή μας μέτρηση. Ξεπέρασαν γρήγορα τη δυσκολία μέτρησης της γωνίας με κορυφή τη βάση του πάσσαλου μεταφέροντας τη γωνία σε μία άλλη θέση ώστε να είναι εντός εκτός και επί τα αυτά δύο παραλλήλων ευθειών.

Πολλοί αναρωτήθηκαν αν τα σημάδια θα είναι σε ευθεία ή όχι. Κατά τη πορεία του ήλιου μέχρι τις 2 που σχολάσαμε διαπίστωσαν ότι η σκιά του πασσάλου μίκραινε μέχρι τις 12.30 και μετά αυξανόταν σχηματίζοντας μια γραμμή που  έμοιαζε κάπως με ευθεία. Στην εφαρμογή που ακολουθεί ρυθμίστε την ημερομηνία, pen down και δείτε τη γραμμή αυτή. Δοκιμάστε και για άλλες ημερομηνίες του χρόνου. Πατήστε ΕΔΩ 

ααα

ΤΟ ΠΕΙΡΑΜΑ ΤΟΥ ΕΡΑΤΟΣΘΕΝΗ ΣΤΟ ΣΧΟΛΕΙΟ ΜΑΣ

Παρασκευή 21 Μαρτίου

Οι μαθητές της Α τάξης ξεκίνησαν από το πρωί και σημείωναν τη σκιά μιας ράβδου μήκους 1 μέτρου κάθε ένα τέταρτο της ώρας σε μία μεγάλη κόλλα χαρτί, που έστρωσαν στο προαύλιο. Σήμερα στήριξαν τη ράβδο σε ειδική βάση και έβαλαν μερικά τούβλα πάνω για να τη σταθεροποιήσουν από το φύσημα του αέρα.

 Όλοι  οι μαθητές των τμημάτων Α1, Α2, Γ1, Γ2 κατέβηκαν 12.15 ετοίμασαν το δικό τους πείραμα και από τις 12.20 για 20 λεπτά κατέγραφαν τις μετρήσεις τους. Σημείωσαν στα χαρτιά τους όλες τις μετρήσεις που χρειάζονταν και αναμένουν μετρήσεις ενός άλλου σχολείου για να προχωρήσουν την εργασία. 

ΟΜΩΣ μπορούμε να υπολογίσουμε την περίμετρο της γης και μόνο από τις δικές μας μετρήσεις ας δούμε πώς;

ΕΡΓΑΣΙΑ ΓΙΑ ΟΛΕΣ ΤΙΣ ΟΜΑΔΕΣ:

Την ημέρα της ισημερίας και την ώρα της μεσουράνησης του ήλιου οι ακτίνες του πέφτουν κάθετα στα μέρη που βρίσκονται στον Ισημερινό. Η σκιά της ράβδου εκείνη τη στιγμή είναι 0 εκατοστά. Σύμφωνα με το σχέδιο που βλέπουμε στην παραπάνω εικόνα η γωνία του ορθογώνιου τριγώνου που σχηματίζεται  από την ράβδο και την ακτίνα του φωτός ισούται με την επίκεντρη γωνία φ της γης. Από την εφαρμογή http://www.daftlogic.com/projects-google-maps-distance-calculator.htm βρίσκουμε την απόσταση μας s από την τοποθεσία που βρίσκεται στο ίδιο γεωγραφικό μήκος με το σχολείο μας αλλά με γεωγραφικό πλάτος 0 (βλέπε εικόνα που ακολουθεί).

Γνωρίζουμε ότι η γωνία μας φ αντιστοιχεί σε ένα τόξο που έχει μήκος s και ότι ένας κύκλος (η γη έχει σφαιρικό σχήμα) αντιστοιχεί σε 360 μοίρες.

Τι λέτε τώρα μπορούμε να βρούμε το μήκος της περιφέρειας της γης; 

Το φύλλο εργασίας συμπιεσμένο ΕΔΩ:  Το_πείραμα_του_Eρατοσθένη_Ardavani

Ευρήματα και ερωτήσεις μαθητών:

1)Το πρωί η σκιά της ράβδου ήταν τόσο μεγάλη; Μπορεί να γίνει πιο μικρή από το μήκος της ράβδου; Να μηδενιστεί;Πότε και πού;

2)Πόσο στρίβει η σκιά του ήλιου όταν μετράμε κάθε τέταρτο της ώρας; Οι γωνίες που ορίζονται είναι ίσες;

3)Το μήκος της σκιάς μικραίνει όσο πλησιάζουμε προς την μεσουράνηση του ήλιου, μετά ξαναμεγαλώνει;

4) Βλέπω ότι η σκιά στις 8.30 ήταν εδώ (δείχνοντας το σημάδι) μέχρι τη δύση του ήλιου πόση γωνία θα γράψει; Πού θα φτάσει;

4)Τα σημάδια της σκιάς της ράβδου βρίσκονται σε ευθεία ή σε καμπύλη;

3)Γιατί ενώ μετράμε κάθε τέταρτο της ώρας τα αντίστοιχα τμήματα που συνδέουν τα άκρα της σκιάς δεν είναι ίσα;

ΤΟ ΣΧΟΛΕΙΟ ΠΟΥ ΣΥΝΕΡΓΑΖΕΤΑΙ ΜΑΖΙ ΜΑΣ:

Από την λίστα των σχολείων που ενεργοποιήθηκαν στο πρόγραμμα βρήκαμε το Transylvania College, Cluj-Napoca , στην Ρουμανία που είχε σχεδόν ίδιο γεωγραφικό μήκος με εμάς. Επικοινωνήσαμε μαζί του και μας εδωσε τις δικές του μετρήσεις για να προχωρήσουμε στον υπολογισμό της περιφέρειας της γης. Μας είπε ότι η δική τους γωνία θ= 46,6 μοίρες. Υπολογίσαμε την απόσταση των δύο σχολείων (γνωρίζουμε τις δικές τους συντεταγμένες) και βρήκαμε 987, 081 Km.

aaa

Οι υπολογισμοί των μαθητών μας σύμφωνα με τις μετρήσεις τους

Οι μαθητές του τμήματος Α1 βρήκαν από το τρίγωνο που σχεδιάσαν με κλίμακα 1:10 τη γωνία θ=36 μοίρες και του Α2 θ=38 μοίρες. Η περίμετρος της γης αντίχτοιχα βρέθηκε 33523 km, 41319 km.

Οι μαθητές των τμημάτων Γ1, Γ2 σχεδίασαν το τρίγωνο με κλίμακα 1:10 και υπολόγισαν τη γωνία θ με χρήση τριγωνομετρικών αριθμών. Βρήκαν ότι η γωνία θ είναι 33 μοίρες και ότι η περιφέρεια της γης είναι26128 km

Ευχαριστούμε τον καθηγητή της τεχνολογίας Κο Μακρογκίκα για την κατασκευή βάσεων των ράβδων, τους γυμναστές του 3ου Λύκειου Γλυφάδας και του 3ου Γυμνάσιου Γλυφάδας για την κατανόηση τους. Ιδιαίτερα ευχαριστούμε τους μαθητές των σχολείων που διακριτικά πλησίαζαν για να πληροφορηθούν το πείραμα και δεν είχαμε μετακίνηση της ράβδου παρά μόνο ελάχιστες φορές από το δυνατό φύσημα του αέρα.

Όποιο σχολείο ενδιαφέρεται, μπορεί να εγγραφεί για τη συμμετοχή του στο πείραμα από εδώ http://eratosthenes.ea.gr/

Πηγή: http://el.wikipedia.org,

http://mathlab.mysch.gr/sundial/ergastiria/eratosthenes,

http://commonmaths.weebly.com/tauomicron-piepsilon943rhoalphamualpha-tauomicronupsilon-epsilonrhoalphatauomicronsigmatheta941nueta.html

Περισσότερα εδώ: http://makolas.blogspot.gr/2013/06/projects.html?view=flipcard

Μερικοί μαθητές της Γ΄ γυμνασίου επισκεφθήκαμε στον ελεύθερο χρόνο μας το μουσείο Ηρακλειδών.  Αρχικά ξεναγηθήκαμε στον φιλόξενο χώρο της έκθεσης και είδαμε αρκετά εκθέματα των Vasarely και  Escher.

Σχήματα σχεδιασμένα σε χαρτί που έδιναν την εντύπωση τρισδιάστατου αντικειμένου αλλά και που μας προβλημάτιζαν.  Ποιο είναι το μπροστινό και ποιο είναι το πίσω μέρος τους; Πόσο δυνατή είναι η πραγματοποίηση της κατασκευής ενός τέτοιου αντικειμένου; Τι κοιτάζει ο ήρωας;  Ποια είναι η δομική μονάδα για τον σχεδιασμό του; Με ποιους γεωμετρικούς μετασχηματισμούς  προέκυψε;   Τελειώνει αυτό ποτέ;  Πόσο πολύ μοιάζει το μέρος με το όλον;

 ααα

Στη συνέχεια καθίσαμε γύρω από ένα τραπέζι και ασχοληθήκαμε με ένα νέο κεφάλαιο μαθηματικών τις πιθανότητες. Μιλήσαμε με τα είδη πειραμάτων: πειράματα με βέβαιο αποτέλεσμα, αιτιοκρατικά και πειράματα με αβέβαιο αποτέλεσμα, τύχης.

Πραγματοποιήσαμε τα παρακάτω πειράματα:

1ο πείραμα τύχης:

Σε ένα μπιμπερό έχουμε 3 μπίλιες 2 κίτρινες και μία πράσινη.  Όταν το γυρίσω ανάποδα βλέπω στο στόμιο του μόνο δύο από αυτές.  Τι  πιθανότητα έχω να δω δύο κίτρινες μπίλιες; Μία πράσινη και μία κίτρινη;

ααα

2ο πείραμα αιτιοκρατικό (χάους)

Ακούσαμε για τα fractals, γεωμετρικά σχήματα με αυτοομοιότητα, που δεν μπορούμε να τα εξηγήσουμε με την ευκλείδεια γεωμετρία και κάναμε ένα πείραμα με ενδιαφέρον αποτέλεσμα:

Πώς θα κατανεμηθούν τα σημεία στο τρίγωνο?

Καθώς η ένδειξη του ζαριού είναι τυχαία κάθε φορά, η διάταξη των σημείων  θα είναι “χαοτική” στο τρίγωνο.  Σωστά ή λάθος?

Μπορείτε να δοκιμάσετε με την εφαρμογή πατώντας στην παραπάνω  εικόνα 

και να βρείτε αναλυτικά οδηγίες για την κατασκευή εδώ

ααα

3ο πείραμα 

Ρίχνουμε 50 ζάρια και ξεχωρίζουμε σε μία στήλη όσα έχουν μονή ένδειξη. Μαζεύουμε τα υπόλοιπα τα ξαναρίχνουμε και ξεχωρίζουμε όσα έχουν μονή ένδειξη και τα τοποθετούμε σε μια στήλη δίπλα από τη προηγούμενη. Επαναλαμβάνουμε μέχρι να τελειώσουν. Τι σχήμα θα φτιάξουν;  γιατί; Τι μας θυμίζει το σχήμα τους από την Άλγεβρα; Τι είδους είναι το πείραμα που κάναμε;

Ηλιόλουστη μέρα και την απολαύσαμε

Γνωρίζουμε το εμβαδόν μιας πισίνας. Μπορούμε να βρούμε τις διαστάσεις της; Πόσες λύσεις έχουμε;
Αν γίνει γνωστό και το άθροισμα των διαστάσεων της μπορούμε να προσδιορίσουμε καλύτερα τις διαστάσεις της; Πόσες λύσεις έχουμε σε αυτή τη περίπτωση;
Ας κάνετε τα πειράματα σας με το αρχείο Geogebra που θα ανοίξει πατώντας πάνω στην εικόνα της πισίνας

Εναλλακτικά μπορείτε να κάνετε λήψη του αρχείου από  ΕΔΩ

Ο Πύργος του Ανόι

ένα ακόμη ενδιαφέρον παιχνίδι. Ο παίκτης πρέπει να μεταφέρει τους δίσκους του πύργου έναν-έναν σε μία άλλη στήλη, έχοντας βοηθητική μία τρίτη στήλη. Ένας σημαντικός κανόνας του παιχνιδιού είναι ότι δεν μπορεί να τοποθετηθεί ούτε μία φορά ένας δίσκος πάνω σε έναν μικρότερο του. 

Πατήστε στην εικόνα που ακολουθεί για να παίξετε. Ξεκινάτε το παιχνίδι με 3 δίσκους στον πρώτο πύργο που πρέπει να τους μεταφέρετε στον τελευταίο (τρίτο πύργο). Μετά ανεβάζετε τη δυσκολία αυξάνοντας τον αριθμό τους.

Μία ενδιαφέρουσα ιστορική παρένθεση σχετικά με τον Πύργο του Ανόι λέει ο παρακάτω θρύλος με τίτλο:

 « Πύργος του Βράχμα »
«Όταν ο Βράχμα δημιούργησε τον κόσμο, έστησε σε ένα ναό στην πόλη Μπενάρες,  64 δακτυλίδια άνισου μεγέθους όλα περασμένα σένα μπαστούνι έτσι ώστε αν κρατήσουμε το μπαστούνι κατακόρυφα να σχηματίζουν τον γνωστό μας πύργο.
Oι ιερείς του ναού έπρεπε να δουλεύουν μέρα νύχτα, χωρίς σταμάτημα, για να μεταφέρουν τα δακτυλίδια σένα άλλο μπαστούνι, χρησιμοποιώντας  ένα τρίτο σαν βοηθητικό, έτσι ώστε να μην τοποθετήσουν μεγαλύτερο δακτυλίδι πάνω από μικρότερο και μετακινώντας ένα μόνο δακτυλίδι σε κάθε κίνηση.
Ο θρύλος λέει πως πριν προλάβουν οι ιερείς να μεταφέρουν όλα τα δακτυλίδια στο άλλο μπαστούνι, ο ναός θα καταρρεύσει μέσα στην σκόνη και ο κόσμος θα χαθεί μέσα σε τρομακτικό κρότο βροντής».

Είχε άραγε ο Βράχμα δίκιο;

Δείτε την απάντηση:

http://3gym-serron.ser.sch.gr/OLDSITE/Anoi.htm 

Περισσότερες προκλήσεις με τον Πύργο του Ανόι εδώ:

http://www.cut-the-knot.org/recurrence/hanoi.shtml

Να δείξετε ότι:

Ι) Αν παράλληλες ευθείες ορίζουν ίσα τμήματα σε μια ευθεία, τότε θα ορίζουν ίσα τμήματα και σε οποιαδήποτε άλλη ευθεία που τις τέμνει.

ΙΙ) Αν από το μέσο μιας μη παράλληλης πλευράς τραπεζίου φέρουμε ευθεία παράλληλη προς τις βάσεις του, τότε αυτή διέρχεται από το μέσο της άλλης μη παράλληλης πλευράς και ορίζει τη διάμεσο του.

ΙΙΙ) Αν από το μέσο μιας πλευράς τριγώνου φέρουμε ευθεία παράλληλη προς μια άλλη πλευρά του, τότε αυτή διέρχεται από το μέσο της τρίτης πλευράς του.

Δοκιμάστε την απόδειξη με τη βοήθεια του αρχείου που ακολουθεί:

✔ Θυμάμαι ποια είναι τα στοιχεία ενός τριγώνου

(κύρια – δευτερεύοντα) και τα είδη των τριγώνων.

✔ Μαθαίνω πότε δύο τρίγωνα είναι ίσα και ποια είναι τα

κριτήρια ισότητας τριγώνων.

• Να χρωματίσετε το εσωτερικό του τριγώνου ΑΒΓ και να γράψετε τα κύρια στοιχεία του.
  κορυφές:  Α ,  …
  πλευρές:  ΑΒ ,  …

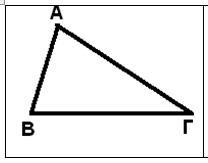
ΘΥΜΑΜΑΙ ΟΤΙ TO ΑΘΡΟΙΣΜΑ ΤΩΝ ΓΩΝΙΩΝ

Α + Β + Γ = …….

και

Η γωνία του τριγώνου που περιέχεται μεταξύ δύο πλευρών λέγεται ………………………… γωνία

Οι γωνίες του τριγώνου που έχουν κορυφές τα άκρα μιας πλευράς λέγονται ………………………………. γωνίες της πλευράς αυτής.

• Να βρείτε τις περιεχόμενες γωνίες μεταξύ των πλευρών

ΑΒ,  ΒΓ :  ………

ΑΒ, ΑΓ :  ……….

ΑΓ, ΒΓ :  ………..

• Να βρείτε τις προσκείμενες γωνίες των πλευρών

ΑΒ :    ……..,   ……….

ΒΓ :     ………,  ……….

ΑΓ :     ….….,  ……….

:
Τα δευτερεύοντα στοιχεία ενός τριγώνου είναι :

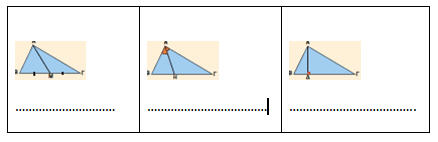
Πατήστε πάνω στη δραστηριότητα που ακολουθεί για να εργαστείτε

ΚΡΙΤΗΡΙΑ   ΙΣΟΤΗΤΑΣ   ΤΡΙΓΩΝΩΝ

ΕΡΓΑΣΙΑ  ΜΕ ΟΜΑΔΕΣ  ΤΩΝ 5-6 ΑΤΟΜΩΝ

Δίνονται τα παρακατω ζευγάρια τριγώνων:

Α)Να κατατάξετε τα ζευγάρια τριγώνων που σας δίνονται στις παρακάτω κατηγορίες.

Ι)Τρίγωνα που έχουν μία πλευρά και δύο γωνίες ίσες

ΙΙ)Τρίγωνα που έχουν δύο πλευρές και μία γωνία ίσες

ΙΙΙ)Τρίγωνα που έχουν τρείς πλευρές ίσες

ΙV)Τρίγωνα που έχουν μία πλευρά και μια γωνία ίσες

V)Τρίγωνα που έχουν δύο πλευρές ίσες

VII)Τρίγωνα που έχουν δύο γωνίες ίσες   ( τρεις γωνίες ίσες)

Β)Να εξετάσετε ποια ζευγάρια τριγώνων είναι ίσα

(Χρησιμοποιήστε ριζόχαρτο ή ψαλιδάκι ή γεωμετρικά όργανα)

και

Γ)Να διατυπώσετε κριτήρια ισότητας τριγώνων

Ι) …

ΙΙ)…

ΙΙΙ)…

ΕΔΩ : Το φύλλο εργασίας μαθητή