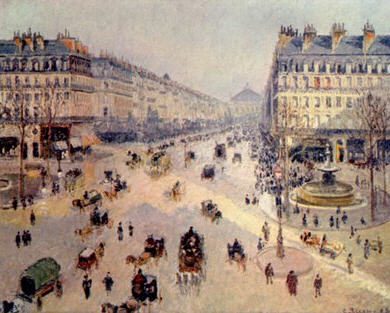ΜΟΥΣΕΙΟ ΗΡΑΚΛΕΙΔΩΝ
Ήταν μία πολύ ενδιαφέρουσα και πρωτότυπη έκθεση που μας προβλημάτισε και μας εντυπωσίασε ταυτόχρονα. Γνωρίσαμε τους ξεχωριστούς και περίεργους πίνακες του Escher και του Vasarely μέσα από μία ενδιαφέρουσα παρουσίαση. Αποκομίσαμε πολλές γνώσεις για την τέχνη αλλά και τη Γεωμετρία. Χάρη στην επιτυχημένη παρουσίαση μεγάλωσε το ενδιαφέρον μας για την τέχνη και τη Γεωμετρία (Ελένη Μ.)
Οι πίνακες ήταν πανέμορφοι και σχεδόν όλοι έκρυβαν ένα “μυστικό”. Ο αγαπημένος μου πίνακας είναι η “σχετικότητα” του Escher , που έδειχνε ανθρώπους πάνω σε μία σκάλα, στο ταβάνι, στο πάτωμα. Αναρωτήθηκα αν και πού θα συναντηθούν άραγε αυτοί οι άνθρωποι; (Νίκος Λ.)
Στην Σχετικότητα, ο Escher όχι μόνο εξέφρασε την ιδέα ότι δεν μπορούν να διορθωθούν οι απόψεις, αλλά επίσης εισήγαγε μια ακόμη ιδέα την οποία θα εξερευνούσε ακατάπαυστα: αυτό που αποτελεί οροφή για τη μια ομάδα, είναι ο τοίχος για την άλλη. Αυτό που αποτελεί πόρτα για τη μια ομάδα, είναι καταπακτή για την άλλη. Όλο το περιβάλλον συνδέεται με ατέρμονες σκάλες, μοτίφο που συνδέεται με τη δουλειά του Escher. Ωθούμαστε από την ανάγκη να ακολουθήσουμε τα μονοπάτια και αν και το μυαλό μας λέει ότι είναι ατέρμονα, τα δεχόμαστε ως αληθοφανή.
Μου δόθηκε η ευκαιρία να παρατηρώ εξωπραγματικούς πίνακες, οι οποίοι συνδυάζουν τα μαθηματικά και την τέχνη. Μπόρεσα να κατανοήσω την ερμηνεία του τριγώνου Penrose καθώς και άλλων αδύνατων κατασκευών. Οι εμπειρίες και οι γνώσεις που απέκτησα είναι μοναδικές.(Δημήτρης Β.)
Το τρίγωνο Penrose είναι ένα τρίγωνο με τρεις ορθές γωνίες. Έτσι τουλάχιστον φαίνεται όταν παρατηρήσει κανείς μία-μία τις τρεις γωνίες του. Είναι όμως δυνατόν να κατασκευάσουμε ένα τέτοιο τρίγωνο; Το βίντεο, που ακολουθεί δίνει την απάντηση.
Μεταξύ των πινάκων μου προκάλεσε μεγάλο ενδιαφέρον ο πίνακας Belvedere. Στον πίνακα αυτό απεικονίζεται ένα τριώροφο κτίριο, το οποίο αν παρατηρηθεί προσεκτικά θα ανακαλυφθούν κάποια παράδοξα. Τα παράδοξα αυτά δίνουν την αίσθηση πως το κτίριο αυτό δεν μπορεί να κατασκευαστεί σε τρεις διαστάσεις, παρά μόνον να σχεδιαστεί στο χαρτί. Υπάρχει όμως περίπτωση το κτίριο αυτό να κατασκευαστεί στην πραγματικότητα. Αυτό είναι και το πιο ενδιαφέρον σημείο. Η απεικόνιση του στο χώρο είναι απλώς …απίστευτη. (Βασίλης Κ.)
Μέσα από τον πίνακα εξερευνάται η ιδέα, πώς το δισδιάστατο επίπεδο επιτρέπει την δημιουργία κτιρίων, τα οποία δεν θα μπορούσαν να υπάρξουν σε έναν τρισδιάστατο κόσμο. Το κτίριο δείχνει να είναι ένα παλάτι, με ένα μπουντρούμι και έναν φυλακισμένο, που κάνει μια γκριμάτσα. Αλλά, παρατηρείστε το μικρό αγόρι στο πρώτο πλάνο – κρατά το κλειδί του γρίφου, έναν κύβο με ανέφικτη κατασκευή. Το κτίριο, που σχεδίασε ο Escher, έχει δύο παράλληλα δάπεδα, ορθογώνια το ένα με το άλλο και κάποιος μπορεί να αναρριχηθεί με ανεμόσκαλα από μέσα προς τα έξω του κτιρίου!
Έγινε μία προσπάθεια να κατανοήσουν οι μαθητές μας ότι όταν ένα αντικείμενο απεικονίζεται στο επίπεδο από μία συγκεκριμένη οπτική γωνία μπορεί να ξεγελάσει το μάτι. Παρατήρησαν το σχήμα του κύβου Necker και τη σκιά του στο επίπεδο, η οποία κάποια στιγμή φαινόταν να ομοιάζει με τον γνωστό μας κύβο.
Παρατηρείστε προσεκτικά και την παρακάτω εφαρμογή:
Ανάβαση και Κατάβαση
Μου άρεσε η επίσκεψη που κάναμε στο μουσείο. Με εντυπωσίασε πάρα πολύ το πείραμα που κάναμε.(Γεωργία Μ.)
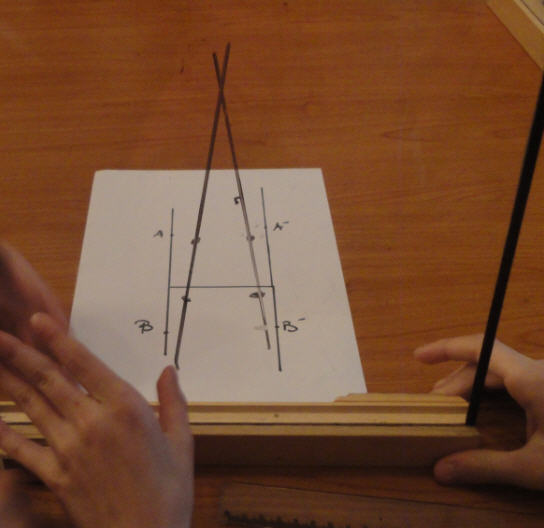
Με λίγα και απλά σύνεργα γίναμε μικροί ζωγράφοι. Προσπαθήσαμε να αποτυπώσουμε όσο πιο πιστά γινόταν στον πίνακα μας ( πλεξιγκλάς) ένα απλό γεωμετρικό σχέδιο, το σχέδιο δύο παράλληλων ευθειών. 



ααα
Το αποτέλεσμα, μας εξέπληξε οι παράλληλες ευθείες που είχαμε σχεδιάσει στο χαρτί απεικονίστηκαν στο πλεξιγκλάς ως τεμνόμενες!
Τι έγινε εδώ; Τι βλέπει το μάτι μας; Πώς έκαναν οι ζωγράφοι στην αναγέννηση τα σχέδια τους δίνοντας την αίσθηση του βάθους σε αυτά;
Είδαμε έναν πίνακα του Pissaro, στον υπολογιστή και εξηγήσαμε το “κόλπο” του ζωγράφου. Δύο ευθείες του δρόμου, παράλληλες από όσο γνωρίζουμε στη πραγματικότητα, τέμνονταν και έδιναν την αίσθηση του βάθους στο σχέδιο!
Δοκιμάσαμε και το αντίστροφο πείραμα. Φωτίσαμε τις τεμνόμενες ευθείες του πίνακα μας και είδαμε τη σκιά τους στο επίπεδο. Ήταν πάλι παράλληλες!
Και ενώ ξεκαθαρίσαμε τα πράγματα και νοιώσαμε ικανοποίηση και χαρά, χαλαρώσαμε και ξαφνικά βρεθήκαμε μπροστά σε ένα νέο γρίφο:
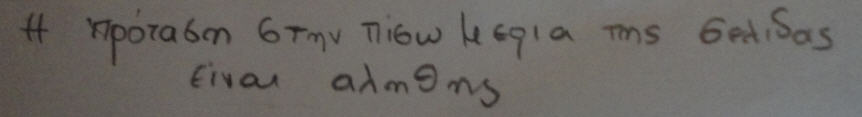
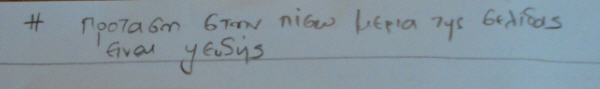 Ποια πρόταση λέει την αλήθεια; Είχαμε δύο προτάσεις στο μπρος και το πίσω μέρος μιας σελίδας, που η μία όμως αναιρεί την άλλη. Είδαμε και έναν πίνακα που έκανε το ίδιο πράγμα αυτοαναφορά, όπως μας είπαν ή αυτοομοιότητα.
Ποια πρόταση λέει την αλήθεια; Είχαμε δύο προτάσεις στο μπρος και το πίσω μέρος μιας σελίδας, που η μία όμως αναιρεί την άλλη. Είδαμε και έναν πίνακα που έκανε το ίδιο πράγμα αυτοαναφορά, όπως μας είπαν ή αυτοομοιότητα.

Στο έργο αυτό, ο Escher παρουσιάζει μια οπτική απάτη! Στη λιθογραφία αυτή, βλέπουμε μια έκθεση χαρακτικών. Στην κάτω αριστερή γωνία, ένας νέος άνδρας κοιτάζει ένα από τα έργα, την απεικόνιση μιας παραλιακής πόλης. Εάν κανείς κοιτάξει κάτω από τα κτίρια στο δεξί μέρος του έργου, θα παρατηρήσει την είσοδο στην πινακοθήκη, πέρα από την οποία βρίσκεται ένας νέος άνδρας ο οποίος κοιτάζει τα χαρακτικά. Έτσι, ο νεαρός είναι ίδιος μέσα στο έργο το οποίο κοιτάζει! Ο Escher δημιούργησε αυτή την αυταπάτη αναπτύσσοντας τη σύνθεση συνολικά 256 φορές κυκλικά, κατά τη φορά των δεικτών του ρολογιού, ξεκινώντας από την κάτω αριστερή γωνία. Ο καλλιτέχνης δεν μπόρεσε να συμπληρώσει την εικόνα στο κέντρο (έβαλε εκεί την υπογραφή του) αλλά τελευταίως ολοκληρώθηκε. Το βίντεο που βλέπετε παρακάτω δείχνει τη λύση του προβλήματος.
Λάτρεψα όλους τους καταπληκτικούς και πρωτότυπους πίνακες που είδαμε και νομίζω πως οι καλλιτέχνες χρειάστηκαν πολύ φαντασία και χρόνο να τους σχεδιάσουν. Κατάλαβα ότι πίσω από έναν πίνακα κρύβονται πολλά πράγματα, που στο παρελθόν δεν τα είχα προσέξει. Θα προσπαθήσω να ξαναπάω. (Γεωργία Μ.)
Είδαμε και φτιάξαμε τη λωρίδα του Mobius. Μία ταινία χαρτί κολλημένη με μία στροφή 180 μοιρών έδινε τη δυνατότητα στο μυρμήγκι να περιηγείται και στις δύο πλευρές της ταινίας προχωρώντας μόνο μπροστά!!!
Η δική μας ταινία τώρα δεν είχε πίσω πλευρά!!! 

Η ξενάγηση ήταν καλή και ο τρόπος που τα εξηγούσε η κυρία με έκανε να καταλάβω τα πάντα. Δεν είχα σκεφτεί ποτέ ότι η τέχνη μπορεί να συνδέεται με τα μαθηματικά. Πέρασα υπέροχα, θέλω να ξαναπάω. ( Μαρία Σ.)
Έχω θετικές εντυπώσεις από την επίσκεψη μου στο μουσείο και θα πρότεινα στον καθένα να το επισκεφθεί.(Ναταλία Μ.)
 Οι εκπλήξεις συνεχίστηκαν στον άλλο όροφο του μουσείου. Είδαμε ωραιότατα γεωμετρικά σχέδια με φωτεινά χρώματα, ενός άλλου καλλιτέχνη του Vasarelly. Κοιτάζοντας ένα από αυτά προσπαθούσαμε να καταλάβουμε ποιο σχήμα μας θυμίζει. Ακούστηκαν 3 διαφορετικές απόψεις. Άλλος έβλεπε ένα κανονικό εξάγωνο, άλλος μία γωνία- κόγχη δωματίου και άλλος ένα δωμάτιο. Τι από όλα ήταν; Παρατηρήσαμε ότι ο καλλιτέχνης σε όλα του τα σχέδια χρησιμοποιούσε 3 ημιάξονες με κοινή αρχή για να δώσει στο μάτι την αίσθηση του τρισδιάστατου αντικειμένου. Τα κατάφερνε εξαιρετικά όμως δεν μας έδινε και την πληροφορία του βάθους ή ήθελε να μας προβληματίσει σε αυτό. Είναι μέσα ή έξω; Πάνω ή κάτω; έχει ύψος ή βάθος; Η απεικόνιση ενός αντικειμένου στο επίπεδο έχει μία διάσταση λιγότερη, μία πληροφορία λιγότερη και από κει αρχίζουν οι παρεξηγήσεις…
Οι εκπλήξεις συνεχίστηκαν στον άλλο όροφο του μουσείου. Είδαμε ωραιότατα γεωμετρικά σχέδια με φωτεινά χρώματα, ενός άλλου καλλιτέχνη του Vasarelly. Κοιτάζοντας ένα από αυτά προσπαθούσαμε να καταλάβουμε ποιο σχήμα μας θυμίζει. Ακούστηκαν 3 διαφορετικές απόψεις. Άλλος έβλεπε ένα κανονικό εξάγωνο, άλλος μία γωνία- κόγχη δωματίου και άλλος ένα δωμάτιο. Τι από όλα ήταν; Παρατηρήσαμε ότι ο καλλιτέχνης σε όλα του τα σχέδια χρησιμοποιούσε 3 ημιάξονες με κοινή αρχή για να δώσει στο μάτι την αίσθηση του τρισδιάστατου αντικειμένου. Τα κατάφερνε εξαιρετικά όμως δεν μας έδινε και την πληροφορία του βάθους ή ήθελε να μας προβληματίσει σε αυτό. Είναι μέσα ή έξω; Πάνω ή κάτω; έχει ύψος ή βάθος; Η απεικόνιση ενός αντικειμένου στο επίπεδο έχει μία διάσταση λιγότερη, μία πληροφορία λιγότερη και από κει αρχίζουν οι παρεξηγήσεις…
 Η υπεύθυνη του μουσείου μας είπε ότι και τα χρώματα που χρησιμοποιούσε μπορεί να λένε κάτι σε μας ή να εκφράζουν ένα συναίσθημα. Oι 4 πίνακες μπροστά μας μπορεί να εκπροσωπούν τις 4 εποχές.
Η υπεύθυνη του μουσείου μας είπε ότι και τα χρώματα που χρησιμοποιούσε μπορεί να λένε κάτι σε μας ή να εκφράζουν ένα συναίσθημα. Oι 4 πίνακες μπροστά μας μπορεί να εκπροσωπούν τις 4 εποχές.
Θα θυμάμαι πάντα την επίσκεψη μου στο μουσείο και εύχομαι στο μέλλον να βλέπω τους πίνακες και να μπορώ να τους εξηγήσω σε μένα αλλά και στους άλλους. (Χρήστος Φ.)
Μου άρεσε που βρέθηκα εκτός σχολείου με τους καθηγητές μου και τις φίλες μου. (Χρύσα Σ.)
ααα
ααα
Μουσείο Ηρακλειδών: http://www.herakleidon-art.gr/el/index.cfm?get=home