Στο μάθημα των μαθηματικών της Β Γυμνασίου, οι μαθητές διδάσκονται στο κεφάλαιο της γεωμετρίας τα κανονικά πολύγωνα. Μαθαίνουν έναν ακόμη ορισμό, μερικούς τύπους και λύνουν ασκήσεις. Κατά πόσο όμως συνειδητοποιούν ότι όλα αυτά τα σχήματα είναι γύρω τους; Κατα πόσο αντιλαμβάνονται ότι τα μαθηματικά δεν είναι αποκομένα από τη καθημερινότητα τους; Θα μπορούσε κανείς να εμπλέξει τους μαθητές σε μια περιπέτεια αναζήτησης, διερεύνησης και ανακάλυψης σχημάτων κανονικών πολυγώνων από το κόσμο γύρω μας;
Τα παραπάνω ερωτήματα αποτέλεσαν την ιδέα της Ιστοεξερεύνησης (Web Quest) http://users.sch.gr/popiardv/webquest/. Απώτερος σκοπός ήταν η σύνδεση των μαθηματικών με τον κόσμο γύρω μας και η αλλαγή στάσης των μαθητών στο μάθημα.
Το πρώτο μάθημα γνωριμίας με το θέμα, πραγματοποιήθηκε στη τάξη και οι μαθητές αναγνώρισαν γεωμετρικά σχήματα πολυγώνων σε εικόνες αντικειμένων που τους δόθηκαν στον διαδραστικό πίνακα. Στη συνέχεια τους ζητήθηκε να κατανείμουν σε δύο ομάδες μια σειρά από πολύγωνα. Υπήρξαν αρκετές προτάσεις ενδιαφέρουσες όπως να τα χωρίσουν σε ανοικτόχρωμα και σκουρόχρωμα ή σε πολύγωνα με μικρό και μεγάλο αριθμό πλευρών.
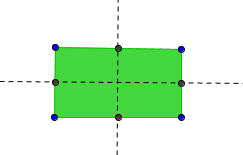
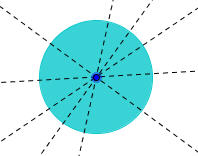
Μερικοί μαθητές παρατήρησαν ότι μερικά πολύγωνα είχαν όλες τις πλευρές μεταξύ τους ίσες αλλά και τις γωνίες τους μεταξύ τους ίσες. Πρόσεξαν δε ότι αυτά τα πολύγωνα έχουν κέντρα και άξονες συμμετρίας άρα ίσως και άλλες «κρυφές» ιδιότητες. Αποφάσισαν να κρατήσουν αυτό το τελευταίο ως κριτήριο διαχωρισμού τους σε δύο ομάδες. Πέρασαν έτσι πολύ ομαλά στον ορισμό κανονικών πολυγώνων και στο επόμενο βήμα ασχολήθηκαν με τον σχεδιασμό τους. Στα τελευταία μαθήματα είχαν ασχοληθεί με τις εγγεγραμμένες και επίκεντρες γωνίες τα αντίστοιχα τόξα τους και είχαν δει σχέσεις μεταξύ τους. Οι μαθητές πρότειναν να χωρίσουν ένα κύκλο σε ίσα μέρη – τόξα και τότε τα ίσα τόξα ορίζουν ίσες χορδές (Πλευρά κανονικού πολυγώνου) και ίσες επίκεντρες γωνίες (Κεντρική γωνία κανονικού πολυγώνου) και όλα αυτά ίσες μεταξύ τους εγγεγραμμένες γωνίες (Γωνία του κανονικού πολυγώνου).
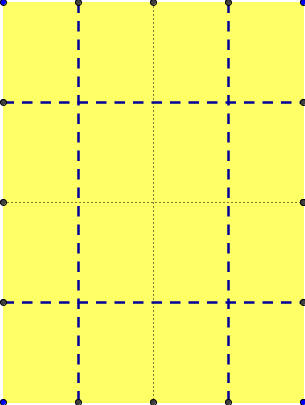
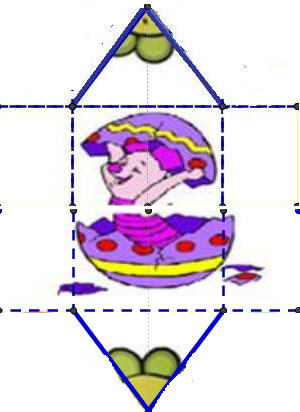
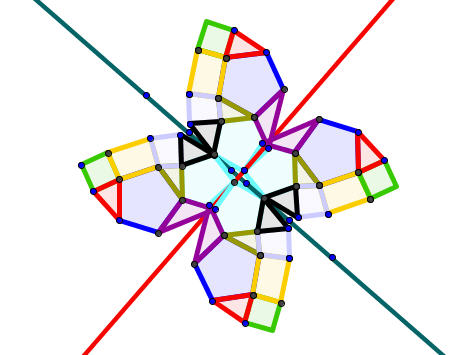
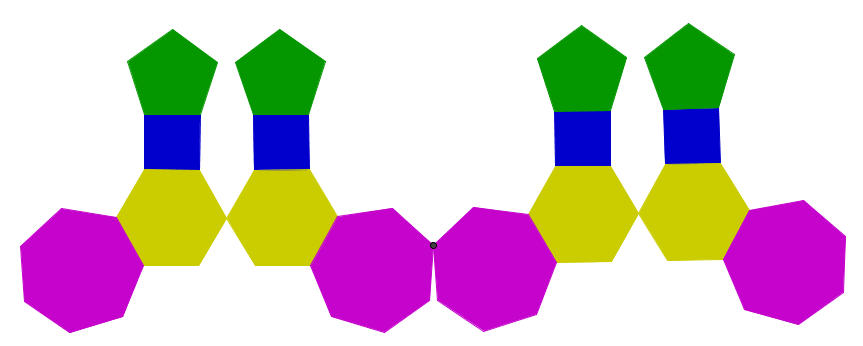
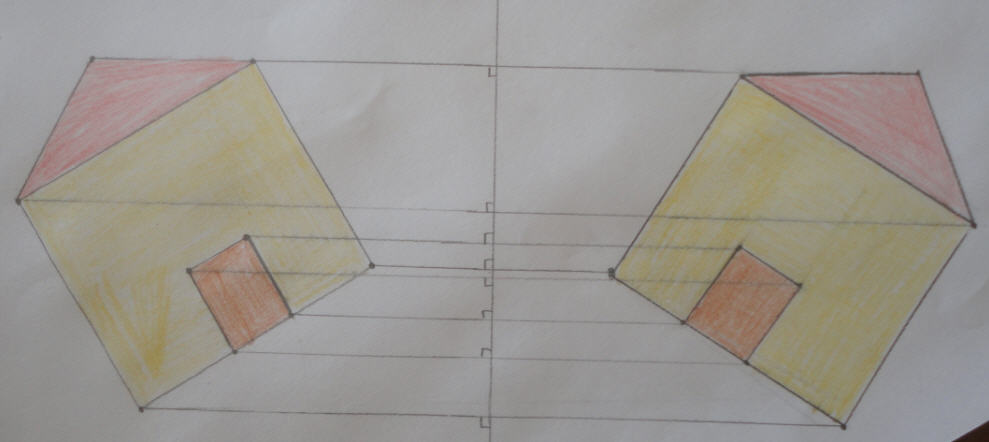
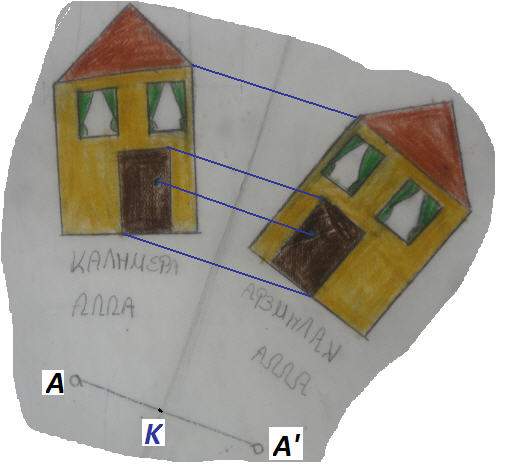
Σχεδίασαν αρκετά κανονικά πολύγωνα και υπολόγισαν στοιχεία τους όπως τη κεντρική τους γωνία και τη γωνία τους και σχέσεις μεταξύ τους. Μερικοί μαθητές διασκέδασαν με αυτά και έκαναν εικαστικές παρεμβάσεις!
Σε επόμενα μαθήματα ενημερώθηκαν για την εργασία που θα έκαναν στο διαδίκτυο και δημιούργησαν ομάδες των 4 -5 ατόμων. Κριτήριο ήταν το να μένουν στην ίδια γειτονιά, και ένας τουλάχιστον μαθητής να διαθέτει υπολογιστή με σύνδεση στο διαδίκτυο.
Δόθηκε η διεύθυνση της εξερεύνησης τους στον ιστόχωρο και οδηγίες για τις συναντήσεις τους. Για ένα περίπου δίμηνο εργάζονταν αν και μερικές ομάδες δυσκολεύτηκαν να συναντηθούν σε ολομέλεια. Για τους περισσότερους ήταν πρωτόγνωρος αυτός ο τρόπος εργασίας – συνεργασίας. Παράλληλα ατο σχολείο ασχολούνταν με την διδακτέα ύλη τους και όχι μόνον, στα κανονικά πολύγωνα και διερευνούσαν τις ιδιότητες τους.
Σε κάθε συνάντηση σπίτι τους, συνέλεγαν ή δημιουργούσαν υλικό το έστελναν στη καθηγήτρια για περαιτέρω καθοδήγηση. Η ομάδα των αρχιτεκτόνων και των καλλιτεχνών συμμετείχαν σε μια συνέντευξη που πραγματοποιήθηκε στο σχολείο με την Μαντικοπούλου Κέλλυ, φοιτήτρια Εσωτερικής Αρχιτεκτονικής, Διακόσμησης και Σχεδίασης Αντικειμένων. του ΤΕΙ Αθήνας. Η ομάδα των μαθηματικών συναντήθηκε ιδιαιτέρως με τον Ελευθερίου Λάμπρο, μαθηματικό που έκανε τη δίμηνη πρακτική του στο σχολείο μας. Η ομάδα των καλλιτεχνών περιηγήθηκε το χώρο του σχολείου με τη συνοδεία του συναδέλφου και διέκριναν αντικείμενα με σχήμα κανονικού πολυγώνου από τα οποία πήραν στιγμιότυπα φωτογραφίες.
Μια αξιόλογη παρατήρηση είναι ότι όλα τα παιδιά διέκριναν στο τέλος της εργασίας τους αντικείμενα που έχουν σχήμα κανονικού πολυγώνου ενώ πολλά παιδιά ακόμη, διέκριναν σχήματα που οι κορυφές τους οι μύτες τους ήταν πάνω σε κορυφές κανονικού πολυγώνου!!!
Με τη λήξη της σχολικής χρονιάς οι μαθητές των δύο τμημάτων Β1 και Β2 του σχολείου μας, παρουσίασαν τα ευρήματα – δημιουργήματα τους: