Απλά ένα ακόμα ιστολόγιο Blogs.sch.gr
26 Ιαν 2013 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Μια ακόμη “απόδειξη” του Πυθαγορείου θεωρήματος με το λογισμικό Geogebra
Παρατηρήστε το σχήμα που σας παρουσιάζεται και το πως εξελίσσεται.
Δοκιμάστε να εξηγήσετε τη σχέση :
ΑΒ^2+ΑΓ^2 =ΒΓ^2
Για να διευκολυνθήτε στην εξήγηση του Πυθαγορείου θεωρήματος ακολουθήστε το ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ: Πυθαγόρειο Θεώρημα
14 Ιαν 2013 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Μια ακόμη οπτική “απόδειξη” του πυθαγορείου θεωρήματος με το λογισμικό Geogebra
Δοκιμάστε:
Aντικείμενα σχεδιασμένα στο επίπεδο
ααα
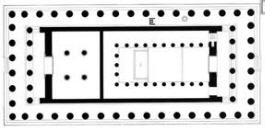
Όταν θέλουμε να απεικονίσουμε ένα αντικείμενο που υπάρχει ή που πρόκειται να κατασκευαστεί, χρησιμοποιούμε το σύστημα των ορθών προβολών. Σχεδιάζουμε την όψη, κάτοψη και τομές του στο χαρτί μας. Σχεδιάζουμε μια σμίκρυνση του αντικειμένου υπό κλίμακα, ώστε να έχουμε ακριβείς πληροφορίες και αντίληψη για τις μορφές και τα μεγέθη σχημάτων, γραμμών και γωνιών του αντικειμένου. Είναι πολύ σημαντικά σχέδια γιατί μπορούμε να παραστήσουμε τη μορφή του χώρου από μέσα. Χρησιμοποιούμε δε σε συνδυασμό όλα μαζί κατόψεις, τομές και όψεις για να πάρουμε ή να δώσουμε το σύνολο των πληροφοριών για ένα χώρο, για ένα αντικείμενο στο χώρο.
Τα παραπάνω συμπληρώνονται με το αξονομετρικό σύστημα προβολών, οι οποίες στηρίζονται στις κατόψεις και τομές του αντικειμένου αλλά μας δίνουν μια τρισδιάστατη μορφή του. Στο αξονομετρικό σύστημα όλες οι παράλληλες γραμμές διατηρούν τη παραλληλία τους καθώς και το μέγεθος τους τα τμήματα.
aaa
Αντιθέτως στο προοπτικό σχέδιο οι παράλληλες γραμμές φαίνεται ότι συγκλίνουν σε ένα σημείο και τα τμήματα δεν κρατούν το μέγεθός τους αφού αυτά φαίνονται μεγαλύτερα όσο πιο κοντά μας βρίσκονται και μικρότερα όσο απομακρύνονται από εμάς. Σε αυτή τη περίπτωση το σχέδιο πλησιάζει περισσότερο σε αυτό που ¨βλέπει¨ το ανθρώπινο μάτι.
ααα
Με λογισμικά του υπολογιστή που αναπτύχθηκαν τα τελευταία χρόνια μπορούμε να έχουμε ένα συνδυασμό δισδιάστατης και τρισδιάστατης εικόνας. Μπορούμε δηλαδή να έχουμε σε μια εικόνα σχεδόν όλες τις πληροφορίες και μια καλή προσομοίωση της πραγματικότητας.
ααα
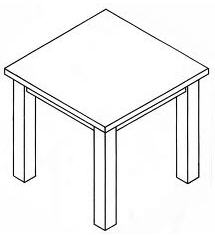
ΣΧΕΔΙΟ ΜΕ ΠΡΟΟΠΤΙΚΗ
Παρατηρώντας το σχήμα του τραπεζιού βλέπουμε τις μπροστινές ακμές μεγαλύτερες από αυτές που είναι στη πίσω πλευρά. Οι ευθείες συγκλίνουν στο σημείο φυγής.
ααα
ΣΧΕΔΙΟ ΜΕ ΑΞΟΝΟΜΕΤΡΙΚΟ ΣΥΣΤΗΜΑ
Αν παρατηρήσουμε καλά το παραπάνω σχέδιο τραπεζιού, βλέπουμε τρεις γραμμές ίσα ευθύγραμμα τμήματα, που σχηματίζουν ανάμεσα τους ίσες γωνίες 120 μοιρών . Οι ακμές του παραμένουν παράλληλες και ίσες.
Ας δούμε πως σχεδιάζοντας ευθύγραμμα τμήματα στο χαρτί μας, δίνουμε στο σχήμα τρισδιάστατη υπόσταση, με αξονομετρικό σύστημα.
Ακολουθήστε τις οδηγίες και απαντήστε στα ερωτήματα. Φανταστήτε, δοκιμάστε, παίξτε, σκεφθήτε και βγάλτε τα δικά σας συμπεράσματα.
Αρκετοί ζωγράφοι, όπως ο Vasarely έπαιξαν με το τρισορθογώνιο σύστημα αξόνων και τα χρώματα. Σχεδίασαν έργα βάζοντας μας σε αμφιβολίες. Το μάτι μας μπερδεύεται μια βλέπει ένα κύβο μέσα σε έναν άλλο και την άλλη ένα κομμάτι κύβου να λείπει από μια γωνία κύβου.
Παρατηρήστε το σχέδιο του Vasarely. Τι βλέπετε; Είσαστε σίγουροι;
29 Δεκ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
ΕΠΑΝΑΛΗΨΕΙΣ
Θέλετε να κάνετε επανάληψη στα μαθηματικά Γυμνασίου; Ας επιλέξετε το βιβλίο σας και στο παράθυρο που ανοίγει το εμπλουτισμένο βιβλίο μαθητή και τη παράγραφο που σας ενδιαφέρει :
Β΄Γυμνασίου:
Α΄Γυμνασίου
ΨΗΦΙΑΚΟ ΣΧΟΛΕΙΟ: http://digitalschool.minedu.gov.gr/
ΠΡΟΣΟΧΗ: Αν έχετε πρόβλημα με τα αρχεία Geogebra (δεν ανοίγουν ή δεν τρέχουν σωστά) να κάνετε λήψη του αρχείου και να το αποθηκεύσετε σε φάκελο του υπολογιστή σας. Ανοίξτε το με το geogebra portable, φορητή εκδοση, που θα το βρείτε στο www.geogebra.org
25 Δεκ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Κ Α Λ Α Χ Ρ Ι Σ Τ Ο Υ Γ Ε Ν Ν Α!
Τελευταία μέρα του 2012 στο σχολείο μας. Οι μαθητές των τμημάτων Β1, Γ1 και Γ3 ασχολήθηκαν με κατασκευές στολιδιών του Χριστουγεννιάτικου δέντρου ή έπαιξαν με το “Οστομάχιον”. Είχαν προμηθευτεί με χαρτονάκια κανσόν, ψαλιδάκια, κόλλες και αυτοκόλητα αστεράκια- χρυσόσκονη. Η έμπνευση για τις κατασκευές ήταν τα φουλερένια και τα πλατωνικά στερεά: τετράεδρο, κύβος, οκτάεδρο, δωδεκάεδρο και εικοσάεδρο.
Τμήμα Β1
Τμήμα Γ1
Τμήμα Γ3
Ερώτημα: Ποια είναι η σχέση των φουλερενιων με τα ημικανονικά πολύεδρα;
Οι καθηγήτριες : Κορίνα Ρόζη, Πόπη Αρδαβάνη.
18 Δεκ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Προγραμματισμός 4ης συνάντησης
Στο σχολείο προγραμματίζουμε τη συνάντηση μας σε υποομάδες για το Γ΄ μέρος της εργασίας μας.
Θα συναντηθούμε στο σπίτι του-της ………………………………………………
την ημέρα ……………………………… και ώρα ……………………..
———————————————————————————————————-
4η συνάντηση
Εργαζόμαστε στις υποομάδες μας και κατασκευάζουμε το δικό μας «Οστομάχιον» με χαρτόνι ή ξύλο.
Παίζουμε λίγο με τα κομμάτια του και φτιάχνουμε δικές μας κατασκευές (σχήματα) με ΟΛΑ τα κομμάτια. Σημειώνουμε οτιδήποτε παρατηρούμε, μας κάνει εντύπωση ή μας δυσκολεύει.
Απαντάμε στα ερωτήματα 17, 18, 19 και 20.
*** Σημειώνουμε στο ημερολόγιο μας τι σημαντικό συνέβη στη συνάντηση μας (έκπληξη, δυσκολία, ανακάλυψη, κλπ)
Παραδίδουμε τα ευρήματα μας (ΦΕ) στη καθηγήτρια.
ΠΡΟΣΟΧΗ: Αν εργαστούμε στο αρχείο Geogebra ΕΔΩ http://www.geogebratube.org/student/m14489 παίρνουμε στιγμιότυπα – φωτογραφίες από τις κατασκευές μας ως εξής.
Πατάμε το κουμπί print screen του υπολογιστή, ανοίγουμε τη ζωγραφική και κάνουμε επικόλληση την εικόνα. Κόβουμε το σχήμα που θέλουμε, το αντιγράφουμε και το επικολλάμε σε ένα νέο αρχείο ζωγραφικής για να το αποθηκεύσουμε ως εικόνα, ή το επικολλάμε απ’ ευθείας στο word ή στη παρουσίαση του Power Point.
Συγκεντρώνουμε όλα τα στιγμιότυπα από την εργασία μας σε ένα αρχείο word ή σε μια παρουσίαση του PowerPoint
Θυμόμαστε να κάνουμε περιγραφή της εικόνας μας κάθε φορά.
Στέλνουμε το αρχείο που φτιάξαμε στην καθηγήτρια μας.
Mail: popiardv…yahoo.com
———————————————————————————————————-
266 συνδυασμοί με διαδοχικές αντιμεταθέσεις δύο κομματιών του Οστομάχιου
ΤΑ ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΜΕ ΤΑ ΕΡΩΤΗΜΑΤΑ 17-20 ΕΔΩ
16 Δεκ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
To 1934 ο Σουηδός καλλιτέχνης Oscar Reutersvärd σχεδίασε ένα τρίγωνο με τρεις ορθές γωνίες. Οπως γνωρίζουμε ένα τρίγωνο μπορεί να έχει το πολύ μία ορθή γωνία. Είναι λοιπόν δυνατόν να υπάρχει στη πραγματικότητα μας ένα τρίγωνο με τρείς ορθές γωνίες; και βέβαια όχι.
Το 1950, ο μαθηματικός Penrose ανακάλυψε αυτό το “αδύνατο τρίγωνο” σαν την αδυνατότητα στη πιο καθαρή της μορφή. Τι συμβαίνει όμως; Πώς οι αισθήσεις μας ξεγελιώνται; πώς μας μεταφέρουν ένα τέτοιο τρίγωνο ως πραγματικό;
Ο καλλιτέχνης Escher εμπνεύστηκε από το τρίγωνο αυτό και το χρησιμοποίησε σε πολλά έργα του για να μας προβληματίσει και να μας μεταφέρει τις ιδέες του.
Ασχοληθήτε με την εφαρμογή που ακολουθεί για να απαντήσετε στα παραπάνω ερωτήματα.
Στο Περθ της Δυτικής Αυστραλίας κατασκευάστηκε το τρίγωνο Penrose δείτε το βίντεο:
Περισσότερα :
Για το τρίγωνο Penrose:
http://mathworld.wolfram.com/PenroseTriangle.html
Για τον Escher και τα έργα του:
http://www.herakleidon-art.gr/el/index.cfm?get=exhibits&show=past&ItemID=31
http://www.herakleidon-art.gr/el/detail.cfm?ItemID=31&PhotoID=105&get=exhibits&StartRow=22
12 Δεκ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
με διασκέδαση και μάθηση.
Διασκεδάστε παρατηρώντας το αστέρι.
Παρατηρήστε από ποια βασικά στερεά σώματα αποτελείται και υπολογίστε την απόσταση δύο μη διαδοχικών κορυφών του.
Πατήστε πάνω στην εικόνα που ακολουθεί:
Εναλλακτικά το αρχείο ΕΔΩ
5 Δεκ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Να δείξετε ότι:
Ι) Αν παράλληλες ευθείες ορίζουν ίσα τμήματα σε μια ευθεία, τότε θα ορίζουν ίσα τμήματα και σε οποιαδήποτε άλλη ευθεία που τις τέμνει.
ΙΙ) Αν από το μέσο μιας μη παράλληλης πλευράς τραπεζίου φέρουμε ευθεία παράλληλη προς τις βάσεις του, τότε αυτή διέρχεται από το μέσο της άλλης μη παράλληλης πλευράς και ορίζει τη διάμεσο του.
ΙΙΙ) Αν από το μέσο μιας πλευράς τριγώνου φέρουμε ευθεία παράλληλη προς μια άλλη πλευρά του, τότε αυτή διέρχεται από το μέσο της τρίτης πλευράς του.
Δοκιμάστε την απόδειξη με τη βοήθεια του αρχείου που ακολουθεί:
30 Νοέ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Στο σχολείο:
Ανταλλάσουμε τα ευρήματα μας στη τάξη και καταλήγουμε στον επανασχεδιασμό του τεμαχισμένου τετραγώνου (ερώτημα 8, 9) με διαστάσεις τέτοιες ώστε, όλες οι κορυφές του να είναι σημεία του πλέγματος.
Βοηθητικά χρησιμοποιούμε το αρχείο Geogebra:
http://www.geogebratube.org/student/m23505
Θα πληροφορηθούμε το όνομα της κατασκευής μας και την ιστορική σημασία της από την καθηγήτρια μας, στο σχολείο (ερ. 11).
Το παλίμψηστο του Αρχιμήδη:
http://users.sch.gr/mmanol/ISTORIA/Palimpstito.pdf
Βλέπουμε το βίντεο με υπότιτλους στα Ελληνικά:
http://www.ted.com/talks/lang/el/william_noel_revealing_the_lost_codex_of_archimedes.html
Στο αρχαίο κείμενο Το “Οστομάχιον” του Αρχιμήδη στίς σελίδες 371 έως 381 εδώ:
http://evangelosstamatis.files.wordpress.com/2011/10/1973-archimides-apanta-tomos-b.pdf
Εργαζόμαστε δουλεύοντας στις υποομάδες μας για να απαντήσουμε τα ερ 12 και 13
Για τους γρίφους του ερ 13: http://www.geogebratube.org/student/m20652
Προγραμματισμός 3ης συνάντησης
Στο σχολείο προγραμματίζουμε τη συνάντηση σε υποομαδες για την ολοκλήρωση του Β΄ μέρους της εργασίας μας.
Θα συναντηθούμε στο σπίτι του-της ………………………………………………
την ημέρα ……………………………… και ώρα ……………………..
———————————————————————————————————-
3η συνάντηση
Εργαζόμαστε στις υποομάδες μας και ολοκληρώνουμε την απάντηση στο ερώτημα 12-13 και συνεχίζουμε στα 14, 15 και 16.
*** Σημειώνουμε στο ημερολόγιο μας τι σημαντικό συνέβη στη συνάντηση μας (έκπληξη, δυσκολία, ανακάλυψη, κλπ)
Παραδίδουμε τα ευρήματα μας (ΦΕ) στη καθηγήτρια.
———————————————————————————————————-
ΤΑ ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΜΕ ΤΑ ΥΠΟΕΡΩΤΗΜΑΤΑ 1-16 ΕΔΩ