Παίζουμε ντόμινο λύνοντας εξισώσεις.
Αρχείο για την κατηγορία 'ΑΛΓΕΒΡΑ'
Εξισώσεις με Ντόμινο
Δημοσιευμένο στην κατηγορία ΑΛΓΕΒΡΑ, Β΄ΓΥΜΝΑΣΙΟΥ στις 26 Απρ 2020
Ενα έξυπνο παιχνίδι για μικρούς και μεγάλους
Δημοσιευμένο στην κατηγορία ΑΛΓΕΒΡΑ, Β΄ΓΥΜΝΑΣΙΟΥ, ΛΥΚΕΙΟ, ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΔΙΑΣΚΕΔΑΣΗ στις 13 Ιαν 2014
Θέλετε να παίξουμε ένα έξυπνο παιχνίδι; Παίζοντας το θα ανακαλύψετε πόσο έξυπνος είναι ο υπολογιστής σας, ότι μπορεί να καταλαβαίνει τι σκέφτεστε και ότι υπάρχουν μαγικά κόλπα…
Ας δούμε όμως πώς παίζεται.
και ακολουθείτε τις παρακάτω οδηγίες πατώντας ![]() :
:
1)Βλέπετε έναν πίνακα με αριθμούς. Πρέπει να διαλέξετε έναν από αυτούς π.χ. ![]() . Μην τον πείτε σε κανέναν, μόνο σκεφτείτε τον με το μυαλό σας.
. Μην τον πείτε σε κανέναν, μόνο σκεφτείτε τον με το μυαλό σας.
2)Παρατηρήστε το χρώμα του αριθμού σας και επιλέξτε το ίδιο χρώμα στη γραμμή με τα χρώματα, που ακολουθεί π.χ. ![]() . Απομνημονεύστε τον αριθμό σας.
. Απομνημονεύστε τον αριθμό σας.
3)Τώρα πρέπει να διαλέξετε ένα από τα παρακάτω χρώματα.  Διαλέξτε αυτό που σας αρέσει.
Διαλέξτε αυτό που σας αρέσει.
4)Μια σειρά από σπιτάκια περιέχουν αριθμούς, έξι διαφορετικούς αριθμούς το καθένα. Βρείτε σε ποιο σπιτάκι βρίσκεται ο αριθμός σας και επιλέξτε το 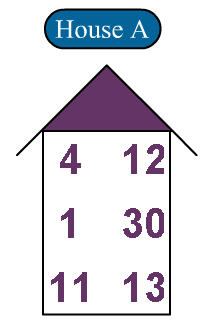 .
.
5)Λίγα μαγικά …. πατήστε πάνω σε μία μπάλα…. Προσέξτε μη μαρτυρήσετε τον αριθμό σας, μην τον πείτε πουθενά. Το μηχάνημα σας ….ίσως σας ακούει …… ίσως λαμβάνει τη σκέψη σας ……ίσως![]() .
.
6)Βλέπετε τρεις πόρτες  Πατήστε πάνω σε μία από αυτές. Μήπως είναι ο δικός σας αριθμός μέσα; Πώς έγινε αυτό;
Πατήστε πάνω σε μία από αυτές. Μήπως είναι ο δικός σας αριθμός μέσα; Πώς έγινε αυτό;
Ωραία περάσαμε, παίξαμε και ξαφνιαστήκαμε με τα … μαγικά. Μήπως όμως πίσω από όλα αυτά κρύβονται τα μαθηματικά; Μήπως μπορούμε να δώσουμε μια εξήγηση; Πώς λειτουργεί το παιχνίδι;
Εναλλακτικά μπορείτε να παίξετε ΕΔΩ
Ο καθένας μας μπορεί να φτιάξει ένα δικό του παιχνίδι και να παίξει με τους φίλους του, προβληματίζοντας τους αρκετά με το πώς βρίσκουμε τον αριθμό που έχουν επιλέξει …
ΑΡΙΘΜΩΝ ΚΑΙ ΣΧΗΜΑΤΩΝ ΔΙΑΛΟΓΟΙ
Δημοσιευμένο στην κατηγορία ΑΛΓΕΒΡΑ, Β΄ΓΥΜΝΑΣΙΟΥ, ΤΕΧΝΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ στις 20 Δεκ 2011
ΝΤΙΝΟΣ ΚΟΡΔΩΣΗΣ
ΑΡΙΘΜΩΝ ΚΑΙ ΣΧΗΜΑΤΩΝ ΔΙΑΛΟΓΟΙ
«Η αρωγή του θεατρικού λόγου στη διδακτική των μαθηματικών»
ΠΡΟΛΟΓΟΣ
Οι ολιγόλεπτοι αυτοί θεατρικοί διάλογοι γράφτηκαν το φθινόπωρο του 2010, σε μορφή σύντομων θεατρικών μαθηματικών δρώμενων και είναι μια απόπειρα, με σκοπό ν’ αξιοποιηθεί η ενάργεια και η δύναμη του θεατρικού λόγου στη διδακτική των μαθηματικών μέσα στην αίθουσα διδασκαλίας. Βέβαια η προσπάθεια αυτή πόρρω απέχει απ’ το να θεωρηθεί, πως φιλοδοξεί να εξελιχθεί σε μέθοδο διδασκαλίας. Μπορεί όμως ν’ αποτελέσει μέρος της διδακτικής πρακτικής του διδάσκοντος, προσφέροντας έναν εύκολο κι ευχάριστο για το μαθητή τρόπο εμπέδωσης της σχετικής παραγράφου, που μόλις έχει ολοκληρωθεί η διδασκαλία της.
Η παρουσίαση των διαλόγων πραγματοποιήθηκε το σχολικό έτος 2010-2011 σε πέντε σχολεία. 59ο, 68ο, 18ο, και 41ο Γυμνάσια Αθηνών, με ορμητήριο το 59ο και ανεξάρτητα στο 65ο Γυμνάσιο Αθηνών. Τα σχόλια διδασκόντων και διδασκομένων ήταν αρκετά θετικά, ώστε να μας δώσουν το κίνητρο, για να επαναλάβουμε την προσπάθεια και την τρέχουσα σχολική χρονιά.
Ευχαριστώ το συνάδελφο Πρωτοπαπά Δημήτριο, Διευθυντή του 59ου Γυμνασίου Αθηνών, για τη συμμετοχή του και τη βοήθεια που μας έδωσε, καθώς και τους συναδέλφους μαθηματικούς, που υπηρετούν στα σχολεία που προαναφέρθηκαν, Τσικρικά Ευσταθία, Σωτηράκου Χαρά, Ασπρουλάκη Πόπη, Αντωνάκο Σωτήριο, Παπαθανασίου Γεώργιο, Κυριακόπουλο Γεώργιο, Μαρκοπούλου Μαρία και Κραβαρίτη Ευαγγελία. Ιδιαίτερα ευχαριστώ τους συναδέλφους Τσουκαλά Ελένη και Οικονομόπουλο Θεόδωρο για την αυθόρμητη συμμετοχή τους και την ανεξάρτητη επιτυχημένη οργάνωση της σχετικής διαδικασίας στο σχολείο τους, 65ο Γυμνάσιο Αθηνών. Επίσης ευχαριστίες οφείλω στο φοιτητή του τμήματος μηχανολόγων του Ε.Μ.Π και πρώην μαθητή μου Κωνσταντίνο Μακαρίου για τη βοήθεια που μου παρέσχε με τον ηλεκτρονικό του υπολογιστή στην αποτύπωση σχημάτων και εικόνων. Τέλος ευχαριστώ την Ελληνική Μαθηματική Εταιρία που ανέλαβε την έκδοση.
Ντίνος Κορδώσης . Αθήνα Σεπτέμβρης 2011
αααα
ΕΞΙΣΩΣΗ
ΤΟ ΔΡΑΜΑ ΕΝΟΣ ΑΓΝΩΣΤΟΥ
Το σκηνικό παρουσιάζει ένα στέκι μαθηματικών οντοτήτων και ειδικότερα το στέκι των μεταβλητών. Ο άγνωστος χ είναι καθισμένος σ’ ένα κάθισμα. Φαίνεται πολύ απογοητευμένος. Σε μια στιγμή πλησιάζει το γκαρσόνι, που το υποδύεται ο ![]()
ΑΓΝΩΣΤΟΣ-Χ Εν ’ αναψυκτικό παρακαλώ!
ΓΚΑΡΣΟΝΙ: Είσαι καλά; Σε βλέπω λίγο χλωμό!
Α-Χ: Φέρε τώρα την παραγγελία κι άστα λόγια!
ΓΚ.: Έγινεε! (To γκαρσόνι φέρνει το αναψυκτικό και κάθεται σε μια καρέκλα δίπλα στον άγνωστο χ). Πάλι μόνος ε;
Α-Χ: Όπως βλέπεις.
ΓΚ.: Δε βαριέσαι! Η μοναξιά είναι η πιο καλή παρέα!
Α-Χ: Το λένε εκείνοι που δεν ένοιωσαν ποτέ τι σημαίνει μοναξιά.
ΓΚ.: Τι να σου κάνω; Είναι βλέπεις η γοητεία που εξασκείς σαν άγνωστος. Όλοι θέλουν να σε ανακαλύψουν.
Α-Χ: Δε μιλάμε για απλή περιέργεια. Πρόκειται για ανελέητο κυνηγητό. Είμαι μονίμως επικηρυγμένος.
ΓΚ.: Α, φίλε μου. Αυτό είναι το τίμημα της επωνυμίας. Ρώτα και μένα που είμαι μονίμως στα αζήτητα. Άρρητος σου λέει ο άλλος, δηλαδή αναξιόπιστος.
Α-Χ: Δεν είναι έτσι.
ΓΚ.: Δυστυχώς έτσι είναι. Ελάχιστες φορές με κάνουν παρέα οι μεταβλητές. Όσο για τους ακέραιους; Προσπαθούν να με κρατάνε σε απόσταση σαν να είμαι μιαρός. Είμαι ο άρρητος με την πιο δημοφιλή στους ανθρώπους υπόριζη ποσότητα και όμως η υπόληψή δεν είναι αντάξια της . Αν δεν εύρισκα τούτη τη δουλίτσα, θα ήμουν τελείως ακοινώνητος.
Α-Χ: Γιατί ποια είναι η δική μου κοινωνικότητα; Η δική μου προκοπή; Με το που θα δοκιμάσω να κάνω παρέα μ’ έναν αριθμό, αμέσως γίνεται επώνυμος. Τον ονομάζουνε συντελεστή μου και προσπαθούν να μας χωρίσουν μ’ αυτή την αναθεματισμένη τη διαίρεση.
2x=12
![]()
x=6
Διαίρεση με το συντελεστή του αγνώστου το λένε. Ύπουλη πράξη η Διαίρεση! Δεν έχει μπέσα!
ΓΚ.: Τι λες;
Α-Χ: Ρε σου λέω δεν μπορώ να κάνω ένα δεσμό της προκοπής. Ν’ αγαπήσω κι εγώ ένα άτομο.
ΓΚ.: Καλά κι εσύ δεν κάνεις καμιά πονηριά;
Α-Χ: Δηλαδή σαν τι πονηριά;
ΓΚ.: Να, να συζευχτείς με αριθμό, αλλά με πράξη μικρότερης βαθμίδας προτεραιότητας. Ας πούμε, σαν την πρόσθεση.
Α-Χ: Λες πως δεν το δοκίμασα κι αυτό; Ορίστε!
x + 2 = 6 κι αμέσως έρχεται η αφαίρεση να μας χωρίσει: x = 6 – 2, δηλαδή
x = 4. Αυτός είναι ο Χωρισμός των γνωστών από τους αγνώστους. Ξέρεις εσύ χωρισμό χωρίς πόνο;
ΓΚ.: Ε, τότε να συνδεθείς με αφαίρεση!
ΑΧ: Μια απ’ τα ίδια είναι. Έρχεται τότε η μαμά της αφαίρεσης η πρόσθεση να μας χωρίσει. Ορίστε! x – 7= 1 και μετά την επίθεση της πρόσθεσης,
x = 1 + 7 και τέλος x = 8
ΓΚ.: Νομίζω ότι χρειάζεται να σχεδιάσεις πιο προσεκτικά τις κινήσεις σου, να μην εμφανίζεσαι παρά σε πολυπληθείς συγκεντρώσεις, για να μη δίνεις στόχο.
Α-Χ: Μου προτείνεις δηλαδή να μετάσχω σε κάποιο ευρύτερο κοινωνικό σύνολο, μήπως και διαλάθω της προσοχής. Το έκανα άπειρες φορές. Χαμένος κόπος! Επιστρατεύουν όλα τα δόλια μέσα, όλα τα όπλα, όλες τις πράξεις για να μ’ απομονώσουν.
ΓΚ.: Πώς δηλαδή;
Α-Χ: Σε πρώτη φάση με δύναμη κρούσης τον πολλαπλασιασμό, που τον συνδράμει η κόρη του η διαίρεση, προσπαθούν να εξαλείψουν τους παρονομαστές στις παραστάσεις που μετέχω.
![]()
πολλαπλασιάζουν και τα δυο μέλη με το ΕΚΠ των παρονομαστών ![]()
Και μετά την απλοποίηση 3 (x – 1 ) + 2 x = 12
Απαλοιφή των παρονομαστών το λένε
ΓΚ.: Ναι, μα δεν σε αποκάλυψαν.
ΑΧ: Μη βιάζεσαι. Ο πολλαπλασιασμός με την αδερφούλα του την αφαίρεση εδώ και σε άλλες περιπτώσεις με τη μαμάκα του την πρόσθεση, συνεργάζονται για να συνεχίσουν το καταστροφικό έργο.
3 x- 3 + 2 x = 12
Επιμεριστική ιδιότητα. Έχει γίνει ο εφιάλτης μου!
ΓΚ.: Είναι αλήθεια πως όλο και σε πλησιάζουν.
Α-Χ: Και τώρα έχει σειρά ο χωρισμός των γνωστών απ’ τους αγνώστους. Στο ένα μέλος οι παραστάσεις που περιέχουν εμένα, στο άλλο οι σταθεροί αριθμοί. Όποιος αλλάζει μέλος, αλλάζει και πρόσημο.
3 x + 2 x = 12 + 3
ΓΚ.: Σατανικό!
Α-Χ: Κι έρχεται τώρα πάλι η επιμεριστική να μ’ απομονώσει τελείως.
( 3 + 2 ) x= 12 + 3 Δηλαδή, 5 x = 15 είναι η περίφημη αναγωγή ομοίων όρων.
ΓΚ.: Φουκαρά μου!
ΑΧ: Και τέλος όπως είδαμε και προηγουμένως, η Διαίρεση μου δίνει τη χαριστική βολή.
![]()
x = 3
Δεν ξέρω πια που να κρυφτώ! Είμαι απελπισμένος.
ΓΚ.: Μα και σένα φίλε μου, τι σ’ έχει πιάσει και κυκλοφορείς πρωτοβάθμιος; αφού το βλέπεις πως όταν είσαι πρωτοβάθμιος είσαι ευάλωτος.
Α-Χ: Κυκλοφορώ και δευτεροβάθμιος αλλά το αποτέλεσμα είναι το ίδιο. Ο δρόμος και τα μέσα που χρησιμοποιούν για να με ανακαλύψουν, είναι πιο μακρύς και πιο επίπονος. Μέχρι και η τετραγωνική ρίζα τίθεται στην υπηρεσία των κυνηγών μου.
ΓΚ.: Μα τότε να μετέχεις σε παραστάσεις με βαθμό μεγαλύτερο
Α-Χ: Δεν είναι τόσο απλά τα πράγματα. Ο μεγάλος εκθέτης είναι βάρος. Με υποβάλλουν σε βασανιστήρια με μηχανές καθώς με κυνηγούν. Μιλάω για μηχανές του ολέθρου, ηλεκτρονικούς υπολογιστές τις λένε ,με ξετρυπώνουν όπου κι αν κρυφτώ. Ύστερα εγώ προτιμώ την απλή ζωή.
ΓΚ.: Με κάνεις να μακαρίζω τον εαυτό μου για την ανωνυμία μου. Τι τα θες και οι επώνυμοι έχουν τα βάσανά τους. Μήπως θες να σου φέρω κι ένα σκέτο καφέ; Θαρρώ πως τον έχεις ανάγκη.
ΤΕΛΟΣ ΔΙΑΛΟΓΟΥ
aaa
ΠΑΡΕΝΘΕΣΕΙΣ ΚΑΙ ΑΓΚΥΛΕΣ
Η ΠΟΛΙΟΡΚΙΑ
ααα
Για να κάνουμε πιο γλαφυρή την παρουσίαση της απλοποίησης μιας αριθμητικής ή αλγεβρικής παράστασης που περιέχει παρενθέσεις και αγκύλες, θα μπορούσαμε να παραλληλίσουμε τις διαδοχικές φάσεις της απαλοιφής, με τις διαδοχικές φάσεις πολιορκίας μιας πόλης. Οι τοίχοι των σπιτιών αντιστοιχούν στις παρενθέσεις. Οι αγκύλες στο τείχος που περιβάλει την πόλη, Τα άγκιστρα (μύστακες) στο εξωτερικό ευρύτερο τείχος κ.ο.κ
Όταν εμπρός από μια αγκύλη υπάρχει το πρόσημο – θεωρείται ως εχθρός που επιτίθεται, γκρεμίζει το τείχος των αγκυλών και όλα τα πρόσημα που ευρίσκονται εκτεθειμένα εκτός των σπιτιών τα αλλάζει. Αντίθετα αν εμπρός από μια αγκύλη υπάρχει το πρόσημο + θεωρείται φίλος και οι πολιορκούμενοι καταργούν το τείχος. Τα εκτεθειμένα πρόσημα στην περίπτωση αυτή παραμένουν ως έχουν. Έχουμε λοιπόν:
α-[β+(γ-α)-(β+γ)-1]=α-β-(γ-α)+(β+γ)+1
Με την ίδια τώρα λογική ο εχθρός (-) γκρεμίζει τον τοίχο του πρώτου σπιτιού, ενώ ο φίλος (+) εμπρός από τη δεύτερη παρένθεση δεν επηρεάζει τα πρόσημα:
α-β-(γ-α)+(β+γ)+1=α-β-γ+α+β+γ+1
ΤΕΛΟΣ ΔΙΑΛΟΓΟΥ
ΠΡΩΤΟΙ ΑΡΙΘΜΟΙ
Η ΜΟΝΑΞΙΑ ΤΗΣ ΚΟΡΥΦΗΣ
Σε κάποιο στέκι αριθμών ο 21 και ο 39 συνομιλούν και σχολιάζουν τον 2, που στέκει πιο πέρα απρόσιτος κι ακατάδεχτος
21:(δείχνοντας στον 39 τον 2) Όταν βλέπω αυτό το νούμερο μου ’ρχεται… ν’ αναριθμήσω τον εαυτό μου!
39: Τον έχει πάρει ψηλά τον αμανέ. Είναι βλέπεις η δομική μονάδα των αρτίων.
21: Βέβαια, αλλά κυρίως για άλλο λόγο ναρκισσεύεται
39: Μπα, για ποιο λόγο;
21: Γιατί είναι πρώτος, και μάλιστα ο μοναδικός άρτιος πρώτος!
39: Σιγά το προσόν!
21: Για σένα και για μένα ίσως δεν είναι, αλλά γι’ αυτόν…
39: Δεν μπορώ να καταλάβω γιατί θα πρέπει κάποιος να επαίρεται που είναι πρώτος. Να υπερηφανεύεται επειδή δεν έχει άλλους διαιρέτες απ’ τον εαυτό του και τη μονάδα.
21: Ας όψεται ο Ευκλείδης!
39: Γιατί ο Ευκλείδης;
21: Γιατί από τη στιγμή που ο Ευκλείδης διατύπωσε κι απέδειξε το θεώρημα, ότι κάθε φυσικός αριθμός μπορεί να εκφρασθεί κατά ένα και μόνο τρόπο σαν γινόμενο πρώτων αριθμών, το καβαλήσανε οι πρώτοι το καλάμι. Μας το παίζουν πια οι δομικοί λίθοι όλων των αριθμών, τα διαμάντια του συνόλου των φυσικών.
39: Ναι, μα θαρρώ πως ο Ευκλείδης απέδειξε επίσης πως οι πρώτοι είναι άπειροι.
21: Αυτό φίλε μου δεν φαίνεται να τους πτοεί. Βλέπεις οι μαθηματικοί, τους δείχνουν σκανδαλώδη αδυναμία.
39: Και πως το διαπίστωσες αυτό;
21: Μετά τον Ευκλείδη, ο Ερατοσθένης πήρε το κόσκινό του και για να διαλέξει τους πρώτους από το σύνολο των φυσικών, έριξε όλους εμάς τους σύνθετους στα σκύβαλα.
39: Ναι μα όσο μεγάλοι μαθηματικοί και να ήταν, δεν ήταν παρά μόνο δυο.
21: Δυστυχώς δεν είναι έτσι. Μετά την αναγέννηση στην Ευρώπη καινούργια υστερική μανία κατέλαβε τους μαθηματικούς για τους πρώτους αριθμούς. Αναζητούσαν μανιωδώς μια φόρμουλα, έναν τύπο, που θα τους έδινε τη δυνατότητα να βρίσκουν πρώτους αριθμούς.
39: Δε μπορώ να καταλάβω τι είναι εκείνο που έχουν οι πρώτοι και γοητεύει τους μαθηματικούς.
21: Το μυστήριο. Γιατί αν και προσπάθησαν, ποτέ δεν μπόρεσαν να βρουν το μαγικό τύπο. Και ασχολήθηκαν με την αναζήτησή του τα μεγαλύτερα μαθηματικά μυαλά της Ευρώπης. Φερμά, Γκάουζ, Όιλερ,Ρίμαν, είναι μερικοί μόνο απ’ τους μεγάλους μαθηματικούς που ασχολήθηκαν με τους πρώτους.
39: Η άρνηση λοιπόν των πρώτων ν’ αποκαλύψουν τη νομοτέλεια με την οποία εμφανίζονται, η άρνηση να υποταχτούν στην ανθρώπινη νοημοσύνη, τους ανέδειξε σε πρώτο μαθηματικό ζήτημα;
21: Ακριβώς.
39: Για να είμαι ειλικρινής τους ζηλεύω αυτούς τους πρώτους.
21: Ε καλά, αυτό πια το ξέρω.
39: και πώς το ανακάλυψες;
21: Σε βλέπω πως αντιμετωπίζεις τους διαιρέτες σου τον 3 και τον 13. Αν μπορούσες θα τους είχες εξαφανίσει από το σύνολο των φυσικών.
39: Κρίνεις φαίνεται εξ ιδίων τα αλλότρια. Το 3 και το 7 σου κάθονται στο στομάχι.
21: Κάνεις λάθος. Απολαμβάνω το γεγονός ότι είμαι σύνθετος, έχω κοινωνικότητα, συγχρωτισμό με τους ομοίους μου εγώ, δεν είμαι μονοκόμματος κι απομονωμένος. Ύστερα αυτούς τους στριφνούς ακοινώνητους πρώτους, τους θεωρώ υπηρέτες.
39: Και γιατί τους θεωρείς υπηρέτες;
21: Γιατί ζεύονται στο ζυγό του πολλαπλασιασμού για να παράγουν εμένα 3•7=21
39: Έτσι όπως το θέτεις…
21: Αφήνω που δε θα άντεχα τη μοναξιά τους.
39: Ποια μοναξιά;
21: Θαρρείς ότι αν ο Ερατοσθένης κοσκίνιζε τους αριθμούς από το 10000000 μέχρι το 10000100 θα του έμεναν πολλοί πρώτοι;
39: Δεν ξέρω.
21: Σε πληροφορώ λοιπόν ότι αν ο πρώτος αριθμός 10000019 νιώσει την ανάγκη να κάνει παρέα με τον επόμενο γείτονά του πρώτο, θα πρέπει να διανύσει πολύ μεγάλη απόσταση για να φτάσει μέχρι τον 10000079. Ενώ για πολύ μεγαλύτερους πρώτους, οι αποστάσεις είναι συνήθως τεράστιες.
39: Φίλε μου με κάνεις να νιώθω τυχερός που είμαι μικρός και σύνθετος.
21: Αυτό είναι το τίμημα της κορυφής για τους πρώτους. Να σκεφτείς ότι οι άνθρωποι για να έρθουν σ’ επικοινωνία μ’ εξωγήινους πολιτισμούς, εκπέμπουν κάποια ακολουθία πρώτων. Αυτοί είναι λοιπόν οι πρώτοι. Χαμένοι στο διάστημα. Η απόλυτη μοναξιά.
39: Δεν ξέρω όμως ποιοι να νιώθουν άραγε μεγαλύτερη μοναξιά, οι πρώτοι αριθμοί, ή οι άνθρωποι;
ΤΕΛΟΣ ΔΙΑΛΟΓΟΥ
aaa
ΣΕΙΧΗΔΕΣ ΚΑΙ ΣΥΝΑΡΤΗΣΕΙΣ
Είναι γνωστό ότι η έννοια της συνάρτησης, μια τόσο θεμελιώδης κι απαραίτητη για τη μελλοντική μαθηματική κατάρτιση γνώση, πολύ δύσκολα γίνεται κατανοητή από τους μαθητές του γυμνασίου. Το αίτημα των μαθητών προ των εξετάσεων του Ιουνίου, «να μας χαρίσετε τις συναρτήσεις κύριε» είναι πολύ συνηθισμένο.
Το παράδειγμα της «μηχανής» που δουλεύει το πρότυπο και παράγει μια και μόνο εικόνα, αν και αρκετά επιτυχημένο, δεν ξεκαθαρίζει και δεν αποτυπώνει με ενάργεια στη μνήμη του μαθητή το γεγονός ότι σε κάθε πρότυπο αντιστοιχεί μια και μόνο εικόνα, ενώ η ίδια εικόνα μπορεί να έχει περισσότερα του ενός πρότυπα. Ο παρακάτω παραλληλισμός όταν δοκιμάστηκε απέδωσε καλύτερα.
Αν πάρουμε σαν σύνολο προτύπων το σύνολο των μουσουλμάνων γυναικών και σαν σύνολο εικόνων το σύνολο των επίσης μουσουλμάνων συζύγων τους, τότε κάθε μουσουλμάνα στοιχείο του πρώτου συνόλου έχει αυστηρά έναν και μόνο σύζυγο, δηλαδή μια και μόνο εικόνα, ενώ κάθε μουσουλμάνος στοιχείο του δευτέρου συνόλου μπορεί να έχει περισσότερες της μιας συζύγους. Δηλαδή στην ίδια εικόνα μπορούν ν’ αντιστοιχούν περισσότερα του ενός πρότυπα, αφού π.χ. ο Χασάν έχει τρεις συζύγους, την Αϊσέ, τη Φατμέ και τη Ραϊφέ, είναι εικόνα τριών προτύπων.
ΤΕΛΟΣ ΔΙΑΛΟΓΟΥ
ΠΟΣΟΣΤΑ
ΤΑ ΠΙΟ ΞΙΠΑΣΜΕΝΑ ΚΛΑΣΜΑΤΑ
Το ![]() και το
και το ![]() βρίσκονται σ’ ένα κατάστημα ειδών ένδυσης την εποχή των εκπτώσεων. Ένας υπάλληλος πηγαινοέρχεται στο χώρο και τακτοποιεί μονολογώντας.
βρίσκονται σ’ ένα κατάστημα ειδών ένδυσης την εποχή των εκπτώσεων. Ένας υπάλληλος πηγαινοέρχεται στο χώρο και τακτοποιεί μονολογώντας.
ΥΠΑΛΛΗΛΟΣ: Όπως πάμε μας βλέπω να βάζουμε λουκέτο. Πρώτη μέρα των εκπτώσεων σήμερα και άνθρωπος δεν πάτησε στο μαγαζί εδώ και ώρες. Έχω να τακτοποιήσω και τη βιτρίνα, μα που το κουράγιο με τέτοιο πεσμένο ηθικό. Ωχ πάλι θα ψάχνουμε για δουλειά… (πέφτει σε μια καρέκλα αποθαρρημένος. Το δέκα εκατοστά και το έξι εξηκοστά, που μπορούν να τους υποδύονται μαθητές με τα αντίστοιχα κλάσματα στο στήθος, έχουν αρχίσει τη λογομαχία).
ΔΕΚΑ ΕΚΑΤΟΣΤΑ: Δεν το βλέπεις; Δεν έχεις καμιά ελπίδα. Πάλι εμένα θα προτιμήσουν. Αποχώρησε οικειοθελώς για να σώσεις τουλάχιστον την αξιοπρέπειά σου.
ΕΞΙ ΕΞΗΚΟΣΤΑ: Και γιατί παρακαλώ θα προτιμήσουν εσένα;
Δ.Ε.: Ε, γιατί εγώ είμαι δεκαδικό κλάσμα, είμαι κομμένο και ραμμένο στα ανθρώπινα μέτρα, πώς να το κάνουμε.
Ε.Ε.: Μα, είμαστε ισοδύναμα κλάσματα, εκφράζουμε το ίδιο μέρος του όλου. Είναι άδικο να προτιμούν συνέχεια εσένα, επειδή κάποιοι απ’ τις Ινδίες έφεραν το δεκαδικό σύστημα αρίθμησης στο προσκήνιο και κάποιος Αλ Μανσούρ, Άραβας χαλίφης το υιοθέτησε.
Δ.Ε.: Έλα τώρα. Το δεκαδικό θεσιακό σύστημα είναι από τις κορυφαίες επινοήσεις του ανθρωπίνου πνεύματος! Ύστερα ο παρονομαστής μου είναι υπερτέλειος.
Ε.Ε.: Σιγά τα λάχανα!
Δ.Ε.: Τι εννοείς;
Ε.Ε.: Ότι κι ο δικός μου παρονομαστής είναι υπερτέλειος και μάλιστα έχει περισσότερους διαιρέτες απ’ τον δικό σου. Ορίστε! Οι διαιρέτες του 60 είναι: 1,2,3,4,5,6,10,12,15,20,30 με άθροισμα: 1+2+3+4+5+6+10+12+15+20+30=108>60, ενώ οι διαιρέτες του 100 είναι: 1,2,4,5,10,20,25,50 με άθροισμα:
1+2+4+5+10+20+25+50=117>100 . Βλέπεις λοιπόν πως και οι δυο αριθμοί είναι υπερτέλειοι αφού είναι μικρότεροι απ’ το άθροισμα των διαιρετών τους, όμως από πλευράς πλήθους και αθροίσματος διαιρετών ο 60 υπερτερεί.
Δ.Ε.: Μα εμένα ο αριθμητής μου είναι η βάση του δεκαδικού συστήματος.
Ε.Ε.: Μήπως δεν είναι κι εμένα ο παρονομαστής μου η βάση του εξηκονταδικού;
Δ.Ε.: (Ειρωνικά). Τι μου θύμησες τώρα! Τις πρώτες ημέρες της δημιουργίας. Τους αρχαίους λαούς της Μεσοποταμίας. Θα σε στενοχωρήσω αλλά πρέπει να το πάρεις απόφαση, πως το εξηκονταδικό σύστημα αρίθμησης ξεπεράστηκε. Πέθανε οριστικά! Είναι πια εν’ απολίθωμα της ανθρώπινης διανόησης.
Ε.Ε.: Μπα! Και το σύστημα μέτρησης των γωνιών με μοίρες; Μια μοίρα διαιρείται σε 60 πρώτα λεπτά, 1 πρώτο λεπτό σε 60 δεύτερα; Ή μήπως πρέπει να σου θυμίσω το χωρισμό της ώρας σε 60 πρώτα λεπτά και του πρώτου λεπτού σε 60 δεύτερα λεπτά
Δ.Ε.: Καλά τώρα! Δεν είναι παρά θλιβερά απομεινάρια του παρελθόντος που θυμίζουν το εξηκονταδικό σύστημα.
Ε.Ε.: Μην το παίρνεις πάνω σου. Μόδα είσαι και η μόδα αντικαθίσταται απ’ την καινούρια μόδα.
Δ.Ε.: Μα κατάλαβέ το επί τέλους! Δεν είσαι παρά ένα συνηθισμένο κλάσμα!
Ε.Ε.: Γιατί, εσύ δεν είσαι ένα συνηθισμένο κλάσμα;
Δ.Ε.: Όχι βέβαια! Εγώ είμαι το ποσοστό!
Ε.Ε: ( Ειρωνικά)Είσαι το ποσοστό.
Δ.Ε.: Είμαι το ποσοστό βέβαια! Ελέγχουμε όλο το τραπεζικό σύστημα εμείς τα ποσοστά. Αγορές, πωλήσεις, δάνεια, αποπληρωμές…
Ε.Ε.: Έχεις δίκιο. Σαν επιτόκια είσαστε όργανα των τοκογλύφων. Στις προεκλογικές δημοσκοπήσεις χειραγωγείτε τη λαϊκή βούληση…
Δ.Ε.: Βλέπεις μόνο τ’ αρνητικά και παραβλέπεις τη μεγάλη προσφορά μας. Οικονομικές δοσοληψίες, εκλογές, και γενικά πολλές απ’ τις υπηρεσίες που προσφέρει η στατιστική θα ήταν δύσκολα προσιτές χωρίς εμάς.
Ε.Ε.: Γιατί δε θα μπορούσαν να χρησιμοποιηθούν άλλα κλάσματα;
Δ.Ε.: Όχι βέβαια, γιατί μόνο τα δεκαδικά κλάσματα είναι εύκολα κατανοητά απ’ τους ανθρώπους. Είναι το σύστημα αρίθμησης που ταιριάζει στα μέτρα τους.
Ε.Ε.: Αυτή η άποψη είναι ένας ατεκμηρίωτος ισχυρισμός.
Δ.Ε.: Καθόλου. Αρκεί να σκεφτείς ότι ο άνθρωπος έχει δέκα συνολικά δάχτυλα στα χέρια, δέκα συνολικά δάχτυλα στα πόδια κι όχι έξι ή εξήντα. Πάρε το απόφαση, στη Γή δεν έχεις καμία τύχη. Μετακόμισε στον πλανήτη με τις εξηνταποδαρούσες.
Ε.Ε.: Είσαι το πιο ξιπασμένο πλάσμα που έχω γνωρίσει!
Δ.Ε.: Μα ξέρεις τι λες; Φαντάζεσαι τον κυρ Μήτσο μπροστά στη βιτρίνα να δει στο παντελόνι πινακίδα που θα αναγράφει: Έκπτωση έξι τοις εξήντα; Θα τρελαθεί ο άνθρωπος!
Ε.Ε.: Γιατί τον συνηθίσανε να τρώει ποσοστά.
Δ.Ε.: Γιατί εμείς τα ποσοστά, είμαστε απλά. Είμαστε κατανοητά. Είμαστε κομψά. Είμαστε…
Ε.Ε.: Σιγά μην έχετε κι αισθήματα ρε! Άντε από κει καλαμοκαβαλημένο κλάσμα! Ποσοστό και κουραφέξαλα! Ένα κλάσμα είσαι και συ τ’ ακούς! Ένα κλάσμα! Αυτό δεν αλλάζει ακόμα κι αν ονομάσεις τον εαυτό σου Φαραώ των αριθμών. (Πλησιάζει ο υπάλληλος κοιτάζει το έξι εξηκοστά και το παραμερίζει).
ΥΠΑΛΛΗΛΟΣ: Ώρα να τακτοποιήσω και κείνες τις πινακίδες στη βιτρίνα πριν επιστρέψει τ’ αφεντικό και με κατσαδιάσει . (στέκεται μπροστά στο έξη εξηκοστά). Μπα! Που βρέθηκε αυτό εδώ; (Ύστερα περνά απ’ το δέκα εκατοστά). Αυτό μάλιστα! (Γράφει σε μια πινακίδα με κιμωλία. Έκπτωση 10%)
Δ.Ε.: (Προς το έξι εξηκοστά). Δε σου τα ’λεγα εγώ; Επέστρεψε τώρα στη σαλαμούρα σου! ( Το έξι εξηκοστά αποχωρεί δαγκώνοντας το δάχτυλό του).
ΤΕΛΟΣ ΔΙΑΛΟΓΟΥ
ΟΛΕΣ ΟΙ ΣΧΕΣΕΙΣ ΕΧΟΥΝ ΤΑ ΠΡΟΒΛΗΜΑΤΑ ΤΟΥΣ
Η γωνία φ είναι η μια από τις δυο κατακορυφήν γωνίες, και συνομιλεί με τη γωνία ω, που είναι η μια από δυο εφεξής και παραπληρωματικές γωνίες
φ: Δεν υπάρχει μεγαλύτερη κατάρα, από το να είσαι κατακορυφήν μιας άλλης γωνίας.
ω: Γιατί είναι κατάρα;
φ: Μα να μη μπορώ να δω τη δίδυμη αδερφή μου! Να έχουμε μόνο ένα κοινό σημείο στην κορυφή του κεφαλιού μας!
ω: Ναι αλλά έχετε και πλεονεκτήματα.
φ: Τι σόϊ πλεονεκτήματα;
ω: Να, είσαστε μονιασμένες. Συμφωνείτε, πώς να το πω;
Οξεία η μια οξεία και η άλλη. Αμβλεία η μια, αμβλεία και η άλλη. Ισότητα είναι αυτή!
φ: Τι λες τώρα; Αφού όταν η μια κοιτάζει κατά την ανατολή, η άλλη κοιτάζει κατά τη δύση. Το βοριά η μια, κατά το νοτιά η άλλη. Εμείς έχουμε την αντίθεση στην ίδια μας την ύπαρξη, αφού οι πλευρές μας είναι αντικείμενες ημιευθείες.
Α-ντι-κει-με-νες!
ω: Ναι, αλλά στην περίπτωση που θα γίνει η κάθε μια σας ευθεία γωνία, συμπληρώνετε τότε μια πλήρη γωνία. Ποιο άλλο συναίσθημα μπορεί να συγκριθεί με το συναίσθημα της πληρότητας;
φ: Άστα! Όσες φορές έγινε αυτό είχαμε πρόβλημα. Μπερδέψαμε τις πλευρές μας. Είδαμε και πάθαμε για να τις ξεμπερδέψουμε.
ω: Ότι και να λες εσύ, είναι πολύ όμορφο να έχεις το ίδιο μέτρο με την αδερφή σου. Πού το δικό μας το δράμα.
φ: Μα εσείς έχετε μια ολόκληρη πλευρά κοινή!
ω: Ίσα- ίσα, αυτή η κοινή πλευρά, έχει γίνει αιτία της συμφοράς μας.
ω: Γιατί;
φ: Γιατί η αδελφούλα μου, η παραπληρωματική μου θέλω να πω, βαριέται εύκολα την κατάστασή της. Πλήττει θανάσιμα. Όταν λοιπόν είναι οξεία, θέλει να γίνει αμβλεία. Σπρώχνει την κοινή μας πλευρά και κει που έχω ξαπλώσει άνετα, έχω βολευτεί κι απολαμβάνω την ευρυχωρία αμβλύτητάς μου, να σου την άλλη στιγμή σαν σφήνα ξυλουργού, στριμωγμένη μέσα σε λίγες μοίρες, να μου κόβεται η ανάσα!
φ: Τι λες;
ω: Όταν συνηθίσω λίγο την κατάστασή μου, και ξαναβολευτώ, να σου και τραβάει η καλή σου την κοινή πλευρά και τεντώνομαι σαν το λάστιχο.
φ: Και δεν τα βρίσκετε να πάψει αυτή η ταλαιπωρία;
ω: Πώς να τα βρούμε εγκλωβισμένες μέσα στην ευθεία γωνία; Ασφυκτιούμε εκεί μέσα!
φ: Θέλω να πω δε συμφωνείτε, να πάρετε η κάθε μια από μισή ευθεία γωνία, να γίνεται ορθές να τελειώνετε;
ω: Αφού σου είπα δε μπορεί η άλλη να μείνει σε μια κατάσταση. Θέλει συνέχεια ν’ αλλάζει. Να σκεφτείς ότι κάποιες φορές πάνω στην απελπισία μου έχω σκεφτεί μέχρι και την αυτοκτονία.
φ: και τι νόημα θα είχε;
ω: Είναι κάποιες φορές που θέλω να την εκδικηθώ. Ν’ αυτοκτονήσω, να μηδενιστώ, για να την καταδικάσω στη σταθερότητα των 180 μοιρών. Θα είναι γι’ αυτήν το αιώνιο βασανιστήριο!
φ: Φουκαριάρα μου! Έχετε και σεις τα προβλήματά σας!
ΤΕΛΟΣ ΔΙΑΛΟΓΟΥ
ΔΕΚΑΔΙΚΗ ΜΟΡΦΗ ΤΩΝ ΑΡΙΘΜΩΝ
ΝΑ ΕΙΣΑΙ ΚΟΜΨΟΣ Η ΝΑ ΕΙΣΑΙ ΑΤΕΛΟΙΩΤΟΣ
Τα κλάσματα ένα τέταρτο ![]() = 0,25 και τρία όγδοα
= 0,25 και τρία όγδοα ![]() = 0,375
= 0,375
συνομιλούν.
ΕΝΑ ΤΕΤΑΡΤΟ: Το ν’ ανήκεις στην καλή κοινωνία του κόσμου των κλασμάτων, έχοντας πεπερασμένο πλήθος δεκαδικών ψηφίων στη δεκαδική σου μορφή, είναι βέβαια πλεονέκτημα, αλλά το να έχεις ένα η δύο μόνο δεκαδικά ψηφία είναι πολυτέλεια, είναι κομψότητα πώς να το κάνουμε.
ΤΡΙΑ ΟΓΔΟΑ: Και τα τρία δεκαδικά φίλε μου, και τα τρία δεκαδικά ψηφία είναι πολυτέλεια και κομψότητα!
Ε.Τ.: Ε, ναι βέβαια! Αν σκεφτεί κανείς τους παρακατιανούς που μας περιστοιχίζουν, σέρνοντας ξοπίσω τους οι ταλαίπωροι την ουρά τους, τα τρία δεκαδικά, είναι… είναι προσόν.
Τ.Ο.: Το παν φίλε μου είναι να έχεις αυτογνωσία, να ελέγχεις την κατάσταση, να γνωρίζεις τα όριά σου!
Ε.Τ.: Ασφαλώως! Γιατί τι να το κάνεις ας πούμε να είσαι δεκαδικό κλάσμα και να σέρνεις ξοπίσω σου τέτοια πεζούρα;
Τ.Ο.: Ναι, αλλά τουλάχιστον τα δεκαδικά κλάσματα έχουν πεπερασμένο πλήθος δεκαδικών ψηφίων στη δεκαδική τους μορφή . Προ ολίγου συνάντησα τον ![]() Αγκομαχούσε ο κακομοίρης να κουβαλήσει το κουφάρι του. Ιδρωμένος κι άκομψος αλλά τουλάχιστον αξιοπρεπής.
Αγκομαχούσε ο κακομοίρης να κουβαλήσει το κουφάρι του. Ιδρωμένος κι άκομψος αλλά τουλάχιστον αξιοπρεπής.
Ε.Τ.: Εντάξει τώρα η κομψότητα δεν είναι αυτή που χαρακτηρίζει τα δεκαδικά κλάσματα, όσο για αξιοπρέπεια …ε, την έχουν κι αυτά την έπαρσή τους.
Τ.Ο.: Εδώ έχουν έπαρση τα κλάσματα που γράφονται σαν περιοδικοί δεκαδικοί. Να κατά φωνή Και τρία έβδομα.( Εκείνη τη στιγμή έρχεται προς το μέρος των συνομιλητών το τρία έβδομα) ![]() = 0,428571428571428571…
= 0,428571428571428571…
ΤΡΙΑ ΕΒΔΟΜΑ: Γεια σας!
Ε.Τ.: Καλώς τον κύριο απειροπόδαρο!
Τ.Ο.: Καλώς τον μηδέν κόμμα τέσσερα δύο οκτώ πέντε εφτά ένα, τέσσερα δύο οκτώ πέντε εφτά ένα, τέσσερα δύο οκτώ πέντε εφτά ένα, τέσσερα δύο οκτώ πέντε εφτά ένα… ( κουνάει τα χέρια του στο ρυθμό αυτό και κάνει τούουου, μιμούμενο τα παλιά καρβουνοκίνητα τρένα.
Τ.Ε.: Διακρίνω μήπως κάποια σκωπτική διάθεση στο καλωσόρισμά σας;
Ε.Τ.: Καλέ πώς σου πέρασε απ’ το νου τέτοια ιδέα; Ίσα-ίσα που είμαστε πολύ σοβαροί. Πως την απόχτησες ρε κακομοίρη αυτή την άσχημη ουρά;
Τ.Ο.: Καλέ ποια ουρά; Εδώ μιλάμε για το τρένο με τα άπειρα βαγόνια! Όλο βγαίνει απ’ το τούνελ και ποτέ δεν τελειώνει.
Τ.Ε.: Καλά ξέρω γιατί τα λέτε αυτά. Έχετε σκάσει απ’ τη ζήλεια σας γιατί τα ψηφία σας έχουν βαρεθεί το ένα το άλλο. Είσαστε τόσο φτωχά, χωρίς ίχνος μυστηρίου.
Ε.Τ.: Δηλαδή εσύ που το έχεις το μυστήριο; Μήπως στην ουρά σου που μοιάζει στην ουρά κροταλία με άπειρα ίδια δαχτυλίδια;
Τ.Ο.: Καλά σου λέει ποιο μυστήριο; Αφού κάθε βαγόνι που βγαίνει απ’ το τούνελ είναι ίδιο με το προηγούμενο.
Τ.Ε.: Ρε δε πα να λέτε σεις! Δεν είμαι ότι κι ότι εγώ. Εγώ μετράω στην πιάτσα! Έχω και θαυμάστριες εγώ.
Ε.Τ.: Πάει την ψώνισε το κακόμοιρο!
Τ.Ο.: Τι έκανε λέει θαυμάστριες; (χα, χα, χα, γελάνε)
Τ.Ε.: Θαυμάστριες και μάλιστα ακέραιες.
Ε.Τ.: Μπα για πες μας ποια ακέραια υπέκυψε στη γοητεία της ουράς σου;
Τ.Ε.: Η εξάδα! Ξέρετε τι κοπλιμέντο μου έκανε τις προάλλες;
Τ.Ο.: Κοπλιμέντο εσένα η εξάδα, η πρώτη τέλεια, που είναι ίση με το άθροισμα των διαιρετών της; 6=1+2+3. Σαν τι κοπλιμέντο;
Τ.Ε.: Με κοίταζε καλά- καλά… αλλά τι λέω με κοίταζε; Μ’ έτρωγε με τα μάτια της έπρεπε να πω και μου είπε: «Παιδί μου ατέλειωτο!»
Ε.Τ.: Καλά ο τύπος είναι μυθομανής!
Τ.Ε.: (αλαζονικά) Και όσες δεν υπέκυψαν στη γοητεία της… ουράς μου, θα υποκύψουν στη γοητεία που μου προσδίδει το καινούργιο κοστούμι που μου σχεδίασαν οι μαθηματικοί.
Τ.Ο.: Τι; Κοστούμι; Ρε τι λέει αυτό εδώ;
Τ.Ε.: Ορίστε: ![]()
Ε.Τ.: Για κοίταξε η ουρά χάθηκε!
Τ.Ο.: Αλήθεια! Σουλουπώθηκε ρε το μπάζο!
Τ.Ε.: Δε γελάτε τώρα ε; Είναι η σειρά μου τώρα να γελάσω! Και γελάει καλύτερα εκείνος που γελάει τελευταίος. Χα, χα,χαα…
ΤΕΛΟΣ ΔΙΑΛΟΓΟΥ
ΕΠΙΚΕΝΤΡΗ ΓΩΝΙΑ ΚΑΙ ΑΝΤΙΣΤΟΙΧΗ ΕΓΓΕΓΡΑΜΜΕΝΗ ΓΩΝΙΑ
«Η πρωτευουσιάνα και οι επαρχιώτισσες»
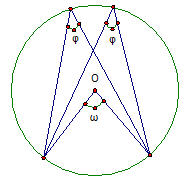
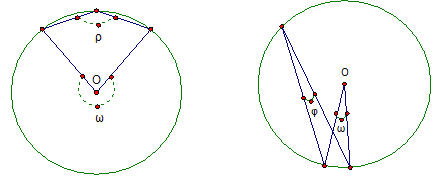
Οι εγγεγραμμένες γωνίες φ και ρ που βαίνουν στο ίδιο τόξο συνομιλούν κουτσομπολεύοντας την αντίστοιχη επίκεντρη γωνία ω. Σε κάποια στιγμή η γωνία ρ απευθύνεται στην γωνία ω που στέκει ακατάδεκτη περιποιούμενη το πρόσωπό της και λιμάροντας τα νύχια της.
ρ: Μπορώ να σ’ απασχολήσω μια στιγμή;… Εε, σε σένα μιλάω μπορώ να σου πω…( Η γωνία ω δεν απαντά).
φ: Σου το είπα! Άδικα απευθύνεσαι σ’ αυτή δεν πρόκειται να καταδεχτεί να σου απαντήσει. Το παίζει η μία και μοναδική βλέπεις, το παίζει η προσωπικότητα. Εμείς είμαστε απλά γωνίες. Η κάθε μια μας εγγεγραμμένη, μια απ’ τις άπειρες που τελούμε «υπό τας διαταγάς της»
ρ: Μα το μόνο που ήθελα να της ζητήσω ήταν το να μη γίνεται μη κυρτή και κυρίως να μην πλησιάζει τις 360 μοίρες, γιατί έχω λίγο τ’ αρθριτικά μου και δεν το μπορώ το σπαγγάτο.
φ: Εμ εγώ που υποφέρω από κοίλη μεσοσπονδυλίου δίσκου, δεν κοψομεσιάστηκα την άλλη φορά που οι μοίρες της έπεσαν σε μονοψήφιο νούμερο. Όσο κι’ αν φώναζα, «φωνή βοώντος εν τη ερήμω» Ρε σου λέω μας το παίζει αριστοκράτισσα! μας το παίζει πρωτευουσιάνα!
ρ: Μπα! Και γιατί αυτό;
φ: Μα γιατί απλούστατα ζει στο κέντρο, ενώ εμείς στην περιφέρεια.
ρ: Έχεις δίκιο, μα τι να κάνουμε; Είμαστε βλέπεις καταδικασμένες σε κείνη την περίφημη σχέση εξάρτησης: «Η εγγεγραμμένη γωνία ισούται με το μισό της αντίστοιχης επίκεντρης».
φ: Την καταραμένη σχέση εξάρτησης θες να πεις!
ρ: Ε, τώρα μην είσαι υπερβολική! Μη βλέπεις μόνο τα’ άσχημα! Για θυμήσου τις περιπτώσεις που η επίκεντρη γίνεται ευθεία γωνία. Τότε το γλεντάμε όλες που γινόμαστε ορθές γωνίες! «Η γωνία που είναι εγγεγραμμένη σε ημικύκλιο είναι ορθή». Σκέτη έκσταση! Θρίαμβος! Μέχρι κι ο Πυθαγόρας ασχολήθηκε μαζί μας!

φ: Τι να το κάνω εγώ; Μια και μοναδική περίπτωση είναι! Αξίζει να ζεις μια ζωή στη μιζέρια, στην αβεβαιότητα της εξάρτησης για μια και μοναδική χαρά κι αυτή όταν ευαρεστηθεί η αφέντρα μας; (ψιθυριστά στη ρ) Εγώ λέω να κάνουμε αγώνα, να τροποποιήσουμε αυτή την ανελέητη για μας σχέση. Δεν μπορεί μια και μοναδική επίκεντρη να λαμβάνει αποφάσεις για άπειρες εγγεγραμμένες.
ρ: Δεν είναι άσχημη ιδέα, αλλά εκ των πραγμάτων μη ρεαλιστική. Για την ακρίβεια η πραγματοποίησή της είναι αδύνατη.
φ: Και γιατί παρακαλώ είναι αδύνατη;
ρ: Για να υπάρξει απόφαση κατά πλειοψηφία, θα πρέπει το πλήθος των ψηφοφόρων να είναι γνωστό. Επομένως πεπερασμένο. Πώς λοιπόν θα γίνει αυτό στην περίπτωσή μας, αφού οι εγγεγραμμένες που αντιστοιχούμε στην ίδια επίκεντρη είμαστε άπειρες;
φ: Ναι, μα εγώ δεν αντέχω άλλο. Θα…θα δραπετεύσω!
ρ: Που θα πας; Αφού το ξέρεις πως για μας τις εγγεγραμμένες ζωή της προκοπής εκτός του κύκλου δεν υπάρχει.
φ: Ε, λοιπόν σου λέω ότι εγώ θα εγκαταλείψω «τον μάταιον τούτο κύκλον»
ρ:Σκέψου το καλά! Τ’ αρνί που φεύγει απ’ το μαντρί το τρώει ο λύκος! Τώρα είσαι τουλάχιστον μια εγγεγραμμένη γωνία, ανήκεις σε κάποιο σύνολο, έχεις μια κοινωνικότητα, μια προστασία μέσα σ’ αυτό. Αν δραπετεύσεις εκτίθεσαι σε κινδύνους. Άλλωστε ξέρεις πως η μοναξιά μπορεί εύκολα να οδηγήσει στην κατάθλιψη…
φ: Λες ε! Μα τότε ίσως θα πρέπει να… το ξανασκεφτώ.
ΤΕΛΟΣ ΔΙΑΛΟΓΟΥ
aaa
Ο ΚΥΚΛΟΣ ΚΑΙ ΟΙ ΑΛΛΟΙ
Στη σκηνή βρίσκεται ένας κύκλος που τον παριστάνει μαθητής που κρατάει πράσινο στεφάνι ρυθμικής γυμναστικής. Ξαφνικά ορμάει στη σκηνή μια μαθήτρια- κύκλος με κόκκινο στεφάνι, βιαστική και λαχανιασμένη σαν να τον κυνηγούν.
ΠΡΑΣΙΝΟΣ ΚΥΚΛΟΣ: Τι έπαθες εσύ και τρέχεις έτσι αλαλιασμένος;
ΚΟΚΚΙΝΟΣ ΚΥΚΛΟΣ: Παρά τρίχα τη γλίτωσα! Παρά τρίχα!
ΠΡ.Κ.: Από τι γλύτωσες; Σε κυνηγούσε κανείς;
ΚΟΚ.Κ.: Ένα παλαβό τετράγωνο με κυνηγούσε για να μέε…
ΠΡ.Κ.: Για να σέε…
ΚΟΚ.Κ.: Για να με τετραγωνίσει!
ΠΡ.Κ.: Μα αιώνες τώρα το επιχειρούν χωρίς αποτέλεσμα. Νόμιζα πως είχαν απογοητευθεί.
ΚΟΚ.Κ.: Φαίνεται πως όχι.
ΠΡ.Κ.: Και πώς έγινε δηλαδή, σου την έπεσε κανονικά;
ΚΟΚ. Κ.: Να, καιρό τώρα με γυρόφερνε. Στην αρχή ευγενικά. Έλεγε πως τάχα το ενέπνεε η ομορφιά της απόλυτης συμμετρίας μου, πως με τις φωτεινές μου ακτίνες φώτιζα το δρόμο της μοναξιάς του.
ΠΡ.Κ.: Τι λες; Και ποιητής ο τύπος.
ΚΟΚ.Κ.: Ε, δεν καταλαβαίνεις; Προσπαθούσε βλέπεις να θίξει τις ευαίσθητες χορδές μου.
ΠΡ.Κ.: Λοιπόν;
ΚΟΚ.Κ.: Ε, ύστερα έγιναν πιο πεζά τα πράγματα. Θέλω να κάνουμε παρέα, να μπω στο στενό φιλικό σου κύκλο… Κι όλο και με πλησίαζε…
ΠΡ.Κ.: Α, το παμπόνηρο τετράπλευρο!
ΚΟΚ.Κ.: Ύστερα άρχισε να μου εφάπτεται…
ΠΡ.Κ.: Α, το ελεεινό ορθογώνιο πράμα!
ΚΟΚ.Κ.: Ύστερα…
ΠΡ.Κ.: Ύστερα μου λέει ξεδιάντροπα και λάγνα: Μάνα μου τι περιφέρεια ειν’ αυτή! Γουστάρω φάση τετραγωνισμού!
ΠΡ.Κ.: Α, το άθλιο τετράγωνο! Και συ τι έκανες;
ΚΟΚ.Κ.: Τι να κάνω; Εκμεταλλεύτηκα την υπεροχή του συντελεστή κυλίσεως έναντι του συντελεστή ολισθήσεως για να εξαφανιστώ και να ’μαι. Δεν ξέρω τι να κάνω! Έχω γίνει κοινός στόχος. Τα ίδια τράβηξα τις προάλλες με μια ξεδιάντροπη ευθεία.
ΠΡ.Κ.: Α, να τις προσέχεις τις ευθείες, είναι οι πιο επικίνδυνες γεωμετρικές υπάρξεις.
ΚΟΚ.Κ.: Εμένα μου λες! Πρωτόγονες! άξεστες! Θρασύτατεες! Είδα κι έπαθα για να γλιτώσω!
ΠΡ.Κ.: Για πες μου πώς έγινε και βρεθήκατε στο ίδιο μέρος;
ΚΟΚ.Κ.: Μ’ αυτές εμφανίζονται ξαφνικά εκεί που δεν το περιμένεις. Όπως έκανα τον περίπατό μου σε μια ημιτονοειδή κατωφέρεια δεν πρόσεξα ότι κατέληγε σε ευθεία και…
ΠΡ.Κ.: Και βρέθηκε η ευθεία σε απόσταση ακτίνας να σου εφάπτεταιαι!
ΚΟΚ.Κ.: Ακριβώς! Και το χειρότερο είναι ότι δεν αρκέστηκε στο ένα κοινό σημείο. Ζήτησε με θράσος να γίνει φορέας μιας χορδής μου.
ΠΡ.Κ.: Κι από χορδή σε χορδή, αφού απόκτησε που απόκτησε απόσταση απ’ την ακτίνα πιο μικρή και δυο κοινά σημεία, ύστερα ήθελε να κάνει μια βόλτα απ’ το κέντρο. Να’ τη λοιπόν την καλή σου φορέα διαμέτρου και συμμετρίας άξονα.
KOK.Κ.: Ακριβώς! Πώς το μάντεψες;
ΠΡ.Κ.: Μα είναι πάγια τακτική της ευθείας.
ΚΟΚ.Κ.: Mου ’γινε κολλιτσίδα. Κατέλαβε το κέντρο και περιορίστηκε σε περιστροφική κίνηση.
ΠΡ.Κ.: Γιατί γύρευε ακόμα ένα χαιβάνι σαν και σένα για να καταλάβει το κέντρο του.
ΚΟΚ.Κ.: Έτσι ε;
ΠΡ.Κ.: Καλά δεν το ξέρεις ότι η ευθεία με το που γεννιέται ονειρεύεται να γίνει διάκεντρος; Τουλάχιστον κοινή εφαπτομένη.
KOK.K.: Σου λέω είδα κι έπαθα να την ξεφορτωθώ και στο τέλος μ’ έβρισε κι από πάνω. Είσαι αντικοινωνικός μου λέει, είσαι φαύλος κύκλος.
ΠΡ.Κ.: Δωσ’του θάρρος του χωριάτη…
ΚΟΚ.Κ.: Εμένα μ’ εντυπωσιάζει το γεγονός ότι όλα τα ευθύγραμμα σχήματα επιδιώκουν να έχουν πάρε δώσε μαζί μας. Αν πεις για τα πολύγωνα, η υπόληψή τους θαρρείς και μεγαλώνει ανάλογα με το πλήθος των πλευρών τους.
ΠΡ.Κ.: Γιατί όσο περισσότερες πλευρές έχουν τόσο περισσότερο προσεγγίζουν τα πρότυπά τους. Δηλαδή εμάς.
ΚΟΚ.Κ.: (ειρωνικά) Άσε μη μου πεις. Το πολύγωνο με το που γεννιέται ονειρεύεται να γίνει κύκλος.
ΠΡ.Κ.: Ακριβώς. Αλλά κύκλος γεννιέσαι, δε γίνεσαι!
ΚΟΚ.Κ.: Και μετριόφρων γεννιέσαι, δε γίνεσαι!
ΠΡ.Κ.: Εκείνο που δυσκολεύομαι να καταλάβω, είναι το γιατί αντιμετωπίζεις εσύ αυτά τα προβλήματα τόσο συχνά
ΚΟΚ.Κ.: Τι εννοείς;
ΠΡ.Κ.: Να, σκέφτομαι, πώς και στην πέφτουν όλοι έτσι στην ψύχρα, μήπως και συ τούς προκαλείς με τη στάση σου; Μήπως κουνάς και συ την ουρά σου;
ΚΟΚ.Κ.: Εγώ τι να προκαλέσω… καλέ ποια ουρά; Εγώ… απλά πηγαίνω στο δρόμο μου.
ΠΡ.Κ.: Δηλαδή πώς πηγαίνεις στο δρόμο σου;
ΚΟΚ.Κ.: Εεε… να έτσι. (Κινείται βηματίζοντας και περιστρέφοντας το στεφάνι γύρω απ’ τη μέση της κάνοντας τη γνωστή κίνηση των γοφών).
ΠΡ.Κ.: (παρακολουθώντας την κίνηση με ειρωνικό ύφος) Έχεις δίκιο δεν προκαλείς. Δεν προκαλείς καθόολου!
ΤΕΛΟΣ ΔΙΑΛΟΓΟΥ
ΤO ΟΝΕΙΡΟ ΤΟΥ ΕΥΚΛΕΙΔΗ
Ο πολλαπλασιασμός, που υποδύεται μαθητής, γράφει στον πίνακα: 56=28•2, 56=14•4, 56=7•8, 56=6•…
ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ: Όχι, όχι, δεν υπάρχει! (Στο χώρο μπαίνει η πρόσθεση που υποδύεται μαθήτρια).
ΠΡΟΣΘΕΣΗ: Τι δεν υπάρχει γιε μου; Πολύ προβληματισμένο σε βλέπω.
ΠΟΛ. : Να, δεν υπάρχει φυσικός αριθμός που να πολλαπλασιαστεί με το 6 και να δώσει γινόμενο 56. Δηλαδή μπορώ να κάνω το 56 μόνο ζευγάρια η εικοσιοκτάδες, δεκατετράδες ή τετράδες, οκτάδες ή εφτάδες, δε μπορώ όμως να το κάνω εξάδες, αφού 6•9=54 και 6•10 =60. Το ίδιο συμβαίνει αν προσπαθήσω να το κάνω πεντάδες, αφού 5•11=55 και 5•12=60… και πάει λέγοντας.
ΠΡ. : Δεν καταλαβαίνω γιατί είναι τόσο σοβαρό αυτό;
ΠΟΛ .: Ε, βέβαια, πώς να με καταλάβεις εσύ, αφού οποιονδήποτε φυσικό αριθμό γουστάρεις, μπορείς να τον εκφράσεις σαν άθροισμα δυο άλλων φυσικών αριθμών.
ΠΡ.: Αυτό συμβαίνει γιατί είμαι η πιο στοιχειώδης, η πιο απλή πράξη.
ΠΟΛ. : Τι εννοείς όταν λες στοιχειώδης;
ΠΡ. : Να, είμαι ας πούμε η πράξη που χρησιμοποίησε πρώτα ο Θεός για να δημιουργήσει τον άνθρωπο. Πρόσθεσε στο χώμα λίγο σάλιο για να φτιάξει τον πηλό, τέλος πρόσθεσε πνοή, κι έτοιμος ο Αδάμ. Ύστερα έκανε την αφαίρεση, αφαιρώντας σάρκα απ’ το πλευρό του Αδάμ για να φτιάξει την Εύα και μετά το παραστράτημα των πρωτοπλάστων, τους έστειλε στη Γή για να κάνουν πολλαπλασιασμό.
ΠΟΛ.: Τι λες;
ΠΡ.: Εγώ λοιπόν κουράζομαι αλλά πάντα πετυχαίνω το σκοπό μου. Εσύ ως μεταγενέστερη πράξη είσαι πιο εξελιγμένος, χρειάζεσαι λιγότερη προσπάθεια, αλλά έχεις και τις αδυναμίες σου.
ΠΟΛ.: Γιαα… γίνε πιο σαφής.
ΠΡ. : Για να εκφράσεις εσύ το 35 με πεντάρια, χρειάζεσαι μια μόνο προσπάθεια: 5•7=35, ενώ εγώ πρέπει να κάνω 6 προσπάθειες: 5+5+5+5+5+5+5=35.
ΠΟΛ. : Ναι αλλά πετυχαίνεις αυτό που θέλεις, ενώ εγώ…
ΠΡ. : Έλα τώρα μη γκρινιάζεις. Θα σε βοηθήσω. Θα ενώσουμε τις δυνάμεις μας και θα τα καταφέρουμε με τη γρηγοράδα του πολλαπλασιασμού και την απλότητα της πρόσθεσης. Είπες πως δε μπορείς να εκφράσεις το 56 σαν γινόμενο του 6 επί κάποιον άλλο φυσικό.
ΠΟΛ.: Ναι δεν μπορώ, γιατί αν επιλέξω το 9 για δεύτερο παράγοντα το 56 υπερτερεί κατά δυο μονάδες του γινομένου 6•9=54.
ΠΡ. : Επομένως θα μπορούσα να βοηθήσω για να εκφράσουμε το 56 ως εξής: 56=6•9+2
ΠΟΛ. : Σωστά, μαα…
ΠΡ. : Τι μα και ξε-μα. Αυτό δεν ήθελες; Να εκφράσεις το 56…
ΠΟΛ. : Να αλλά σαν γινόμενο του 6 επί κάποιον άλλον παράγοντα.
ΠΡ. : Ε, Δε γίνεται. Ορίστε η μητέρα σου, σου προσφέρει τη συνεργασία της, αν θέλεις τη δέχεσαι.
ΠΟΛ. : Απ’ ότι φαίνεται δεν μπορώ να κάνω κι αλλιώς, δεν μπορώ να χωρίσω το 56 σε ενιάδες, ή σε εξάδες…
ΠΡ. : Είπες να χωρίσω;
ΠΟΛ. : Ναι, να χωρίσω, να κομματιάσω, να διαμερίσω το 56 σε εξάδες ή ενιάδες…
ΠΡ.: Δηλαδή το να κόψεις το 56 σε κομμάτια καθορισμένου μεγέθους δε γίνεται πάντα.
ΠΟΛ.: Ακριβώς. Αν θέλουμε να εκφράσουμε το 56 έτσι ώστε στο γινόμενο να παίρνουν μέρος το 6 και το 9, θα πρέπει στο γινόμενο 6•9 να προσθέσουμε και το 2. Επομένως αυτό που κάνουμε δεν είναι πρόσθεση ή πολλαπλασιασμός.
ΠΡ. : Σωστά. Θα μπορούσαμε να πούμε πως είναι μια καινούρια πράξη.
ΠΟΛ. : Και βέβαια πιο εξελιγμένη, άρα και με περισσότερες αδυναμίες.
ΠΡ. : Τώρα μπήκες στο πνεύμα.
ΠΟΛ. : Κι αφού τη χρησιμοποιούμε για να διαμερίσουμε το όλο, να την πούμε Διαίρεση.
ΠΡ.: Τον αριθμό που πρέπει να διαμεριστεί θα πρέπει να τον ονομάσουμε Διαιρετέο, και το πλήθος των μερισμάτων να το πούμε Διαιρέτη.
ΠΟΛ.: Δηλαδή στην περίπτωσή μας Διαιρετέος είναι το 56 και διαιρέτης είναι το 6. Άρα το 9 που το αναζητούμε ώστε να πλησιάσουμε με το γινόμενο το 56 όσο το δυνατόν περισσότερο, χωρίς να το ξεπεράσουμε, θα πρέπει σύμφωνα μ’ αυτή την καταπληκτική ελληνική γλώσσα να τον ονομάσουμε πηλίκο. Και το 2 πώς θα πρέπει να ονομαστεί;
ΠΡ. : Προφανώς υπόλοιπο, αφού είναι η ποσότητα που υπολείπεται το γινόμενο 6•9 για να φθάσει το 56.
ΠΟΛ.: Έχουμε λοιπόν: 56=6•9+2 Γενικά αν συμβολίσουμε τις ποσότητες που λαμβάνουν μέρος με τα αρχικά των ονομάτων τους έχουμε : Δ=δ•π+υ όπου βέβαια το υπόλοιπο θα είναι πάντοτε μικρότερο του διαιρέτη. υ<δ
ΠΡ. : Εντάξει. Aς δούμε αν λειτουργεί. (Η πρόσθεση κι ο πολλαπλασιασμός κάθονται κάπου παράμερα, ενώ στο χώρο ορμούν με φασαρία οι ποσότητες : Διαιρετέος, διαιρέτης, πηλίκο και υπόλοιπο. Τον Διαιρετέο και το διαιρέτη υποδύονται μαθητές που έχουν στα μπλουζάκια τους τα αντίστοιχα σύμβολα, ενώ το πηλίκο και το υπόλοιπο μαθήτριες. Ο Διαιρετέος που κατά προτίμηση υποδύεται ένας εύσωμος βαρύς τύπος, ξαπλώνει σε μια ξαπλώστρα με αργές κινήσεις, επίσης κάθεται κι διαιρέτης. Το πηλίκο παραμένει όρθιο, ενώ το υπόλοιπο που μπορεί να υποδύεται μια μικρόσωμη κινητική μαθήτρια, τριγυρίζει στο χώρο σαν σβούρα χειρονομώντας ζωηρά και διαμαρτύρεται έντονα).
ΥΠΟΛΟΙΠΟ: Κατάλαβες φίλε μου; Είμαι το κλωτσοσκούφι εδώ μέσα!.. Του κλώτσου και του μπάτσου!..του κλώτσου και του μπάτσου!
ΠΗΛΙΚΟ: ( Στο υπόλοιπο) ησύχασε πια και στάσου σ’ ένα μέρος, μας ζάλισες!
ΥΠ.: Να ησυχάσω; Αυτή την πολυτέλεια την έχουν μόνο οι αφεντάδες (δείχνει Διαιρετέο και διαιρέτη) και οι βολεμένοι.(δείχνει το πηλίκο).
ΠΗΛ. : (ενοχλημένα).Υπονοείς κάτι; Δεν κατάλαβα!
ΥΠ. : Εννοώ ότι είμαι ο πιο υποβαθμισμένος, ο πιο αδικημένος, δέσμιος των ορέξεων όλων, εκείνος που κάνει τις αγγαρείες εδώ μέσα. Πως θέλεις να το δεχτώ αδιαμαρτύρητα;
ΠΗΛ. : Αδικημένος; Δέσμιος; Δηλαδή ποιανού είσαι δέσμιος;
ΥΠ.: Του διαιρέτη βέβαια. Δεν μ’ αφήνει να κινηθώ ελεύθερα. Είμαι υποχρεωμένος να είμαι μικρότερός του. Έτσι και τολμήσω να εξισωθώ μαζί του, μετατρέπομαι αυτόματα σε μηδενικό, ενώ του λόγου σου αυξάνεσαι κατά μια μονάδα. Αυτή δεν είναι ζωή, είναι σκλαβιά!
ΠΗΛ. : Τι να σου κάνω φίλε μου όλοι έχουμε τις γονιδιακές μας αδυναμίες. Μήπως εγώ δεν είμαι εξαρτημένος απ’ αυτά εκεί τα δυο ξαπλωμένα βουτυρόπαιδα; Ρε τραβιέμαι σου λέω σαν το λάστιχο! Έτσι και του καθίσει του διαιρέτη ν’ αυξηθεί εγώ αυτόματα ελαττώνομαι, αν του ’ρθει να ελαττωθεί εγώ αυξάνομαι.
ΥΠ. : Δε σου τα ’λεγα εγώ πως ο διαιρέτης είναι ο κακός μας δαίμονας;
ΔΙΑΙΡΕΤΗΣ: Α, για σταθείτε. Τι νομίζεται πως εγώ είμαι προνομιούχος, πως δεν έχω περιορισμούς εγώ;
ΥΠ. : Ρε, το παιδί μίλησε! Έχει και θράσος ο τύπος!
ΠΗΛ. : Δηλαδή τι περιορισμούς έχεις;
ΔΙΑΙΡΕΤΗΣ: Πρώτον, σπάνια μπορώ να ξεπεράσω το Διαιρετέο.
ΠΗΛ. : Ε, αυτό εγώ δε μπορώ ποτέ να το πετύχω.
ΥΠ. : Κοίτα ρε, κλαίνε τώρα οι χήρες κλαίνε και οι παντρεμένες! Κλαίει η γενιά των ανέργων και των πεντακοσίων ευρώ κλαίνε και οι βουλευτές ως κακά αμειβόμενοι.
ΔΙΑΙΡΕΤΗΣ: Και το χειρότερο…(Κρύβει με τις παλάμες του το πρόσωπο) το χειρότερο είναι…
ΠΗΛ. : Ποιο είναι το χειρότερο;
ΔΙΑΙΡΕΤΗΣ: Το χειρότερο είναι πως δεν έχω… δεν έχω το δικαίωμα ν’ αγγίξω το μηδέν… δεν έχω το δικαίωμα εφ’ όρου ζωής ν’ αγγίξω το μηδέν Αααα! (Κάνει πως κλαίει)
ΥΠ. : Κοίταξε υποκρισία! Μας παριστάνει τώρα και το θύμα!
ΠΗΛ.: Ε, μην είσαι και συ τόσο άτεγκτο. Φαίνεται πως στ’ αλήθεια έχει πρόβλημα.
ΥΠ.: Ωραία! Και ποιος ευθύνεται για τις συμφορές μας;
ΠΗΛ.: (Δείχνοντας τον Διαιρετέο) Μόνο αυτός απόμεινε, άρα αυτός ευθύνεται!
ΔΙΑΙΡΕΤΑΙΟΣ: πώς;
ΔΙΑΙΡΕΤΗΣ: (Δείχνοντας κι αυτός τον Διαιρετέο) Αυτός εκεί ποιος άλλος!
ΔΙΑΙΡΕΤΑΙΟΣ: Εγώ;
ΥΠ.: Ρε σεις έχετε δίκιο. Σίγουρα αυτόος! Αυτός που μας το παίζει άνετος ευθύνεται!
ΔΙΑΙΡΕΤΑΙΟΣ: (Ανήσυχος) . Τι λέτε, τρελαθήκατε όλοι σας;
ΥΠ. :Να τον λιντσάρουμε εδώ και τώρα! Εμπρός πάνω του! (Κινούνται απειλητικά προς το μέρος του διαιρετέου που σηκώνεται να φύγει πανικόβλητος. Εκείνη τη στιγμή επεμβαίνουν η πρόσθεση κι ο πολλαπλασιασμός).
ΠΡ. : Ε, σεις φρόνιμα! Δε σας φταίει ο Διαιρετέος!
ΥΠ. : Και τότε ποιος φταίει;
ΠΟΛ. : Κανείς βέβαια! Παρά μόνο ο τρόπος που βλέπετε τα πράγματα.
ΠΗΛ. : Δηλαδή είναι ζήτημα φιλοσοφίας;
ΠΡ. : Ακριβώς. Εσύ υπόλοιπο πρέπει να λάβεις υπ’ όψη σου ότι έχεις το πλεονέκτημα να σχετίζεσαι με το μηδέν. Όσο για το διαιρέτη και το πηλίκο με λίγη διπλωματία θα μπορούσαν να εναλλάσσονται στους ρόλους, οπότε θα έχουν τη δυνατότητα να σχετίζονται με το μηδέν, και να δίνουν στο υπόλοιπο περισσότερες δυνατότητες.
ΔΙΑΙΡΕΤΗΣ: (Προς το πηλίκο).Αυτό είναι αλήθεια. Πώς δεν το σκεφτήκαμε;
ΠΗΛ.: Τι να σου πω, δεν ήξερα πως είσαι τόσο αλτρουιστής, ώστε να μου παραχωρήσεις το ρόλο σου και δεν καταλαβαίνω τι θα πει διπλωματία.
ΠΟΛ.: Πηγαίνετε λοιπόν τώρα στη δουλειά σας χωρίς φασαρίες και καβγάδες. (δ,π,και υ φεύγουν αλλά ο Διαιρετέος κοντοστέκεται).
ΔΙΑΙΡΕΤΕΟΣ: Δεν πάω εγώ με τους τρελούς. Αυτοί εκεί με μισούν.
ΠΡ: Πήγαινε δεν κινδυνεύεις . Ξέρουν πως η ύπαρξή τους προυποθέτει τη δική σου ύπαρξη. (Ο διαιρετέος φεύγει) Τελικά το να μοιράσει κανείς ρόλους δεν είναι καθόλου εύκολη υπόθεση. Όλο και κάποιος θα είναι δυσαρεστημένος.
ΠΟΛ.: Ωραία τα καταφέραμε. Θα πρέπει όμως να δώσουμε τίτλο σε τούτο το μικρό θεατρικό δρώμενο.
ΠΡ.: Πανεύκολο. Θα τ’ ονομάσουμε « το όνειρο του Ευκλείδη»
ΠΟΛ.: Καλά ακούγεται αλλά… έχω μια ένσταση.
ΠΡ. : Ποια ένσταση;
ΠΟΛ. : Να, αυτά που είπες για το Θεό και τους πρωτόπλαστους… Ο Ευκλείδης ήτανε κάποιους αιώνες πεθαμένος όταν έγινε η μετάφραση των εβδομήκοντα. Άρα δεν γνώριζε τα περί γενέσεως του πρώτου κεφαλαίου της Αγίας γραφής.
ΠΡ. : Μα όταν πρόκειται για ένα νου σαν του Ευκλείδη, η συμβατική έννοια του χρόνου καταργείται. Δεν υπάρχει πια πριν και μετά, δεν υπάρχει ροή του χρόνου προς μια κατεύθυνση.
ΠΟΛ .: Εντάξει λοιπόν ας ονομαστεί «τ’ όνειρο του Ευκλείδη»
ΤΕΛΟΣ ΔΙΑΛΟΓΟΥ
Επικοινωνία με τον Ντίνο Κορδώση: ntinoskkk@yahoo.gr
Αυτοαξιολόγηση στις ανισότητες
Δημοσιευμένο στην κατηγορία ΑΛΓΕΒΡΑ, Β΄ΓΥΜΝΑΣΙΟΥ στις 13 Δεκ 2011
Θυμόμαστε τις βασικές ιδιότητες των ανισοτήτων
1)Αν α < β τότε α + γ < β + γ
2)Αν α < β τότε α – γ < β – γ
3)Αν α < β τότε α * γ < β * γ, γ>0
4)Αν α < β τότε α * γ > β * γ, γ<0
Δομάζουμε να διαπιστώσουμε αν τις κατανοήσαμε;
Πρέπει να τοποθετήσετε τα πλακάκια ντόμινος σε μια σειρά,
ώστε κάθε ανισότητα σε αριστερό πλακάκι να συνδέεται με μια άλλη στα δεξιά της, που προκύπτει από αυτή. Προσοχή στο παράδειγμα: 
έτοιμοι για την αυτοαξιολόγηση ;
Δημιουργός Πόπη Αρδαβάνη, ΠΕ03
Αχ αυτές οι ανισότητες!!!
Δημοσιευμένο στην κατηγορία ΑΛΓΕΒΡΑ, Β΄ΓΥΜΝΑΣΙΟΥ στις 8 Δεκ 2011
Το σύμβολο της ανισότητας είναι : > ή < . Πως το διαβάζουμε;
Ας προσπαθήσουμε να εξηγήσουμε μερικές βασικές ιδιότητες των ανισοτήτων παίρνοντας το μοντέλο της ίδιας μας της ζωής, το μεγάλωμα μας στο χρόνο.
Ο ‘Αγγελος, α ετών είναι μικρότερος σε ηλικία από τον φίλο του τον Βασίλη, β ετών και ο Βασίλης είναι μικρότερος από τον κοινό φίλο τους τον Γιάννη, γ ετών. Ποιος είναι ο πιο μεγάλος από τους τρεις φίλους; Ισχύει ότι α < β και β < γ άρα ο Βασίλης έχει ηλικία β ανάμεσα από τις ηλικίες α και γ δηλαδή α < β < γ οπότε α < γ δηλαδή ο μεγαλύτερος σε ηλικία είναι ο Γιάννης!
Οι μαθητές δυσκολεύονται να καταλάβουν ότι πρέπει να προσθέσουν ή να αφαιρέσουν τον ίδιο αριθμό γ και από τα δύο μέλη μιας ανισότητας και δεν κατανοούν την ομόστροφη ανισότητα που προκύπτει.
Υποθέτουμε ότι ο Δημήτρης 14 ετών έχει ένα αδελφάκι που πηγαίνει στο δημοτικό, τον Γιώργο . ‘Εστω ότι η ηλικία του Γιώργου είναι α τότε η σχέση που γνωρίζουμε για τις ηλικίες των δύο αδελφών είναι : α < 14.
Στο ερώτημα ποια σχέση θα έχουν οι ηλικίες τους μετά από 5 χρόνια θα μπορούσαμε να απαντήσουμε ότι α+5<19 αφού ο Γιώργος τότε θα είναι α+5 ετών και ο Δημήτρης 14+5=19 ετών. Μετά από γ χρόνια; Τότε πάλι θα ισχύει α+γ<14+γ αφού οχρόνος μεγαλώνει και τους δύο το ίδιο.
Αν τώρα πούμε ότι η ηλικία του Δημήτρη είναι β ετών τι θα μπορούσαμε να πούμε για τις ηλικίες τους μετά από γ χρόνια;
Αν α < β τότε α+γ < β+γ αφού μεγαλώνουν γ χρόνια και οι δύο, δηλαδή ποτέ δεν θα γίνουν συνομήλικοι ή ο Γιώργος μεγαλύτερος από τον μεγάλο του αδελφό τον Δημήτρη!
Ομοια θα μπορούσαμε να ρωτήσουμε ποια ήταν η σχέση των ηλικιών τους πριν δύο χρόνια; πριν γ χρόνια; Αν α < β τότε α – γ < β – γ
Ποια η σχέση των ηλικιών τους σε διπλάσια χρόνια; σε γ-πλάσια χρόνια; Αν α < β τότε α * γ < β * γ, γ > 0
Δυο φίλοι ηλικίας α και γ πηγαίνουν στο δημοτικό και τα μεγαλύτερα τους αδέλφια τους ηλικίας β και δ στο Γυμνάσιο. Τι ισχύει για το άθροισμα των ηλικιών των δυο φίλων α, γ; το αθροισμα των ηλικιών των δύο φίλων είναι μικρότερο από το άθροισμα των ηλικιών των δυο μεγάλων αδελφών τους δηλαδή:
α < β και γ < δ τότε α + γ < β + δ
Μήπως τώρα έγιναν περισσότερο κατανοητές οι ιδιότητες των ανισοτήτων; Ας δοκιμάσουμε να απαντήσουμε σε μερικά ερωτήματα:
1)αν χ<5 τότε χ+3 < …..
2)αν χ<7 τότε χ-3 ……….
3)αν χ>11 τότε 2χ ………..
4)αν ψ>4 τότε ψ/2 ………
5)αν t<8 τότε 3t+5 ……….
6)αν 5<κ και 7>κ τότε ………
7)αν μ<9 και ν >9 τότε ……….
Αυτοαξιολόγηση στις εξισώσεις με ντόμινο
Δημοσιευμένο στην κατηγορία ΑΛΓΕΒΡΑ, Β΄ΓΥΜΝΑΣΙΟΥ στις 1 Δεκ 2011
Ας κάνουμε την αυτοαξιολόγηση μας στις εξισώσεις α΄βαθμού με έναν άγνωστο.
Προσοχή στο παιχνίδι αυτό της αυτοαξιολόγησης έχουμε μόνο 5 λεπτά στη διάθεση μας. Κάθε προσπάθεια μας βαθμολογείται θετικά (σωστό) ή αρνητικά (λάθος).
Αρχίζουμε επιλέγοντας ένα πλακάκι του ντόμινο τυχαία. Λύνουμε την εξίσωση που βλέπουμε δεξιά του και το ταιριάζουμε με το πλακάκι που έχει τη λύση αυτής της εξίσωσης στα αριστερά του.
Επαναλαμβάνουμε το ίδιο μέχρι να ταιριάξουμε όλα τα πλακάκια.
Προτείνεται να είμαστε σε φυλλομετρητή Internet Explorer
και από εκεί να πατήσουμε τον παρακάτω σύνδεσμο:
εναλλακτικά από internet explorer ακολουθούμε τον σύνδεσμο :
http://www.kubbu.com/student/?i=1&a=19256_activity_titl
NEO ΕΔΩ: https://blogs.sch.gr/popiardv/archives/1708
Δημιουργός: Πόπη Αρδαβάνη, ΠΕ03
ΚΑΛΗ ΕΠΙΤΥΧΙΑ!
ΕΞΙΣΩΣΕΙΣ α΄ΒΑΘΜΟΥ ΜΕ ΕΝΑΝ ΑΓΝΩΣΤΟ
Δημοσιευμένο στην κατηγορία ΑΛΓΕΒΡΑ, Β΄ΓΥΜΝΑΣΙΟΥ στις 30 Οκτ 2011
Το μάθημα αυτό πραγματοποιείται σε αίθουσα με διαδραστικό πίνακα, με τα φύλλα εργασίας μαθητή και με τη βοήθεια έτοιμων εφαρμογών ζυγαριάς.
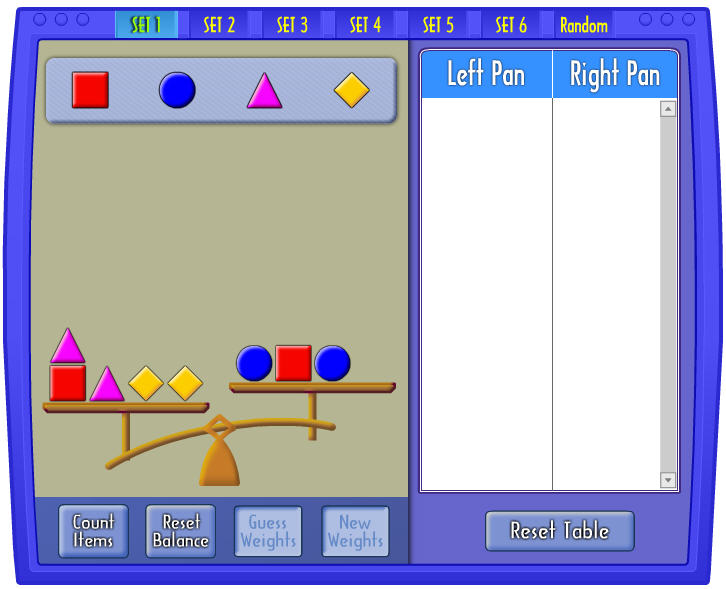
Α’ ΜΕΡΟΣ: Οι μαθητές πειραματίζονται με τη ζυγαριά, ¨ζυγίζουν¨ πακέτα και απαντούν ένα – ένα τα ερωτήματα στο φύλλο εργασίας τους. Ανακαλύπτουν τις ιδιότητες των ισοτήτων, εμπλέκονται στην έννοια της ισορροπίας του ζυγού – εξίσωσης. Βρίσκουν το βάρος ενός πακέτου όταν γνωρίζουν το βάρος ενός άλλου εφαρμόζοντας τις ιδιότητες που ανακάλυψαν προηγούμενα .
Φτιάχνουν μια σχέση ισορροπίας στη ζυγαριά χρησιμοποιώντας δυο ειδών πακέτα της εφαρμογής, χρησιμοποιούν τον ποσοτικό μετρητή αντικειμένων, μαθηματικοποιούν τη σχέση ισορροπίας και φτιάχνουν την εξίσωση που περιγράφει το φαινόμενο, ονομάζοντας το βάρος του άγνωστου με τη βοήθεια μιας μεταβλητής, πακέτο βάρους χ. Περιγράφουν τα βήματα που οδηγούν στη λύση της εξίσωσης, εφαρμόζοντας τις ιδιότητες που έχουν ανακαλύψει.
Β’ ΜΕΡΟΣ: Παίρνουν μια δεδομένη εξίσωση με άγνωστο μια μεταβλητή ας πούμε χ και φτιάχνουν την αντίστοιχη σχέση ισορροπίας στο ζυγό. Χρησιμοποιούν ιδιότητες ισοτήτων για να προσδιορίσουν την τιμή του άγνωστου χ. Επεκτείνουν τις σχέσεις ισότητας και για αρνητικά πακέτα ή αριθμούς με την εφαρμογή, όπου τα αρνητικά πακέτα ή οι αρνητικοί αριθμοί παριστάνονται με μπαλόνια. Περιγράφουν τα βήματα που οδηγούν στη λύση της εξίσωσης, εφαρμόζοντας τις ιδιότητες που έχουν ανακαλύψει.
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
Θα βρείτε ένα ενδεικτικό φύλλο εργασίας ΕΔΩ: ζυγος_final : με τη χρήση της εφαρμογής ζυγαριάς ΕΔΩ για τα ερωτήματα Ι έως και VIII, την εφαρμογή ΕΔΩ για τα ερωτήματα IX και X και την εφαρμογή ΕΔΩ για τα ερωτήματα ΧΙ και ΧΙΙ
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
Α΄ΜΕΡΟΣ
ΙΔΙΟΤΗΤΕΣ ΙΣΟΤΗΤΩΝ
Ι)Τοποθετήστε τα πακέτα στη ζυγαριά και συμπληρώστε το κατάλληλο σύμβολο: = , >, < .
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
ΙΙ)Αν στο αριστερό μέρος της ζυγαριάς τοποθετήσουμε τα πακέτα ![]() (ποσότητα α) και στο δεξιό το πακέτο
(ποσότητα α) και στο δεξιό το πακέτο ![]() (ποσότητα β)
(ποσότητα β)
τι παρατηρείτε; Λέμε ότι η ζυγαριά …………………. δηλαδή
| α … β |
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
Κρατάμε τα πακέτα που βρίσκονται στη ζυγαριά και συνεχίζουμε …
ΙΙΙ) Τοποθετούμε και στα δύο μέλη μια ποσότητα ίδιων πακέτων, ας πούμε γ
Τοποθετούμε …………………… στο αριστερό και ……………………. στο δεξιό μέρος του ζυγού.
Εχουμε α= β=
Ο ζυγός ισορροπεί? ………………….
Συμπεραίνουμε ότι :
| αν α … β τότε α …γ ………. β ….γ |
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
IV) Βγάζουμε και από τα δύο μέλη μια ίδια ποσότητα πακέτων, ας πούμε γ.
Βγάζουμε ………………………… από το αριστερό και ……………………….. από το δεξιό μέρος του ζυγού.
Εχουμε α= β=
Ο ζυγός ισορροπεί? ………………….
Συμπεραίνουμε ότι :
| αν α … β τότε α …γ ………. β…..γ |
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
V) Διπλασιάζουμε και τα δύο μέρη του ζυγού
Εχουμε α= β=
Ο ζυγός ισορροπεί? ………………….
Συμπεραίνουμε ότι :
| αν α … β τότε α * 2 ………. β * 2 |
| αν α … β τότε α * 3 ……… β * 3 |
Γενικότερα
| αν α … β τότε α …γ ……….. β…..γ |
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
VI) Σε κάθε μέρος του ζυγού αφήνουμε τη μισή ποσότητα.
Έχουμε α= β =
Ο ζυγός ισορροπεί? …………………
Συμπεραίνουμε ότι :
| αν α … β τότε α : 2 ………. β : 2 |
Γενικότερα
| αν α … β τότε α …γ ………. β…..γ | με | γ ≠ 0 |
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
ΥΠΟΛΟΓΙΣΜΟΣ ΤΟΥ ΑΓΝΩΣΤΟΥ, ΜΕ ΤΗΝ ΕΦΑΡΜΟΓΗ ΙΔΙΟΤΗΤΩΝ ΤΩΝ ΙΣΟΤΗΤΩΝ – ΕΝΝΟΙΑ ΤΗΣ ΕΞΙΣΩΣΗΣ
VII) α) Υπολογίστε το βάρος του μπλε πακέτου αν το κόκκινο ζυγίζει 3 κιλά. 
Τρόπος σκέψης και ενεργειών
1)Αφαιρούμε και από τα δύο μέρη της ζυγαριάς ………………..
2)Αφαιρούμε το ….. και από τα δύο μέρη
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
β) Υπολογίστε το βάρος του κίτρινου πακέτου αν το κόκκινο ζυγίζει 2 κιλά. 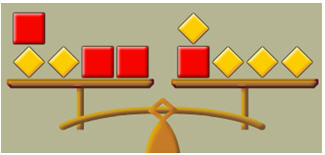
1)Αφαιρούμε και από τα δύο μέρη της ζυγαριάς ………………..
2)Αφαιρούμε το ….. και από τα δύο μέρη
3)Κάνουμε ……….. ομοίων όρων
5)Διαιρούμε και τα δύο μέλη με το …….
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
γ)Υπολογίστε το βάρος του μπλε πακέτου αν το ροζ ζυγίζει 1.5 κιλό. 
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
ΟΡΙΣΜΟΣ ΤΗΣ ΕΞΙΣΩΣΗΣ α΄ βαθμού με έναν άγνωστο και ΥΠΟΛΟΓΙΣΜΟΣ ΤΟΥ ΑΓΝΩΣΤΟΥ χ
VIII) Χρησιμοποιήστε τον μετρητή αντικειμένων (count items) και γράψτε τη σχέση ισορροπίας του ζυγού 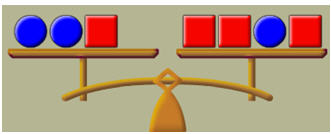
Αν ονομάσουμε το άγνωστο βάρος του πακέτου ![]() =
= ![]() ενώ το βάρος του πακέτου
ενώ το βάρος του πακέτου ![]() είναι 2 κιλά, πως μπορεί να ξαναγραφτεί η σχέση του προηγούμενου ερωτήματος;
είναι 2 κιλά, πως μπορεί να ξαναγραφτεί η σχέση του προηγούμενου ερωτήματος;
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
ΙΧ)Ονομάζουμε το ![]() = χ και ξαναγράφουμε τη σχέση του προηγούμενου ερωτήματος.
= χ και ξαναγράφουμε τη σχέση του προηγούμενου ερωτήματος.
Να υπολογίσετε τη τιμή του αγνώστου χ.
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
Η παραπάνω σχέση ισότητας λέγεται …………………….. με
…………………………… τη ………………………. X και λύση X =………….
Κάθε εξίσωση έχει …… …………………
το α ……………… και το β …………………….
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
B’ ΜΕΡΟΣ
ΕΠΕΚΤΑΣΗ και ΜΕΘΟΔΟΛΟΓΙΑ ΕΠΙΛΥΣΗΣ ΤΗΣ ΕΞΙΣΩΣΗΣ
Χ) Τοποθετήστε κατάλληλα πακέτα , ![]() ,
, ![]() στα δύο μέρη της ζυγαριάς ώστε να ισχύει η ισότητα: 3 (χ + 1) = 6 + χ.
στα δύο μέρη της ζυγαριάς ώστε να ισχύει η ισότητα: 3 (χ + 1) = 6 + χ.
Υπολογίστε τη τιμή του χ
Υπόδειξη : Μετασχηματίστε την εξίσωση
στη μορφή α χ + β = γ χ + δ
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
ΧΙ)Τοποθετήστε κατάλληλα πακέτα ![]() ,
, ![]() ,
, ![]() ,
, ![]() στη ζυγαριά ώστε να ισχύει η εξίσωση α) 3 χ – 2 = 4 και να υπολογίσετε τη τιμή του αγνώστου χ.
στη ζυγαριά ώστε να ισχύει η εξίσωση α) 3 χ – 2 = 4 και να υπολογίσετε τη τιμή του αγνώστου χ.
Όμοια για τις επόμενες
β)3 χ – 4 = χ
γ)3 χ – 2 = – χ + 6
δ)3 χ – 3 = 0
ε) – 3 ( χ – 3 ) = χ + 1
ζ) 2 ( χ – 1 ) + 3 ( 2 – χ ) = 4 ( χ + 2 )
Υπόδειξη :
Μετασχηματίστε την εξίσωση στη μορφή α χ + β = γ χ + δ
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
ΣΗΜΑΝΤΙΚΟΣ ΣΤΟΧΟΣ:
Να χωρίζω γνωστούς από αγνώστους
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
Γράφω οδηγίες για τη λύση εξίσωσης :
1) Κάνω όλους τους πολλαπλασιασμούς
2)Αφαιρώ κατάλληλες ποσότητες και από τα δύο μέρη της εξίσωσης
(ΧΩΡΙΖΩ ΓΝΩΣΤΟΥΣ ΑΠΟ ΑΓΝΩΣΤΟΥΣ)
3)Κάνω αναγωγή των ομοίων όρων
4)Διαιρώ με τον συντελεστή του αγνώστου και τα δύο μέλη της εξίσωσης
5)Βρίσκω τη τιμή του αγνώστου
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
ΧΙΙ)Να λυθούν οι εξισώσεις : α)3( χ -1) +7 = χ
β)(χ + 1) /2 + χ = (2χ + 3) /3 +2
γ)χ+1 =χ
δ)χ+1=1+χ
ΥΠΟΔΕΙΞΗ: Να προετοιμάσετε τις εξισώσεις κατάλληλα ώστε να γίνουν της μορφής α χ + β = γ χ + δ
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
ΧΙΙΙ)ΑΣΚΗΣΗ
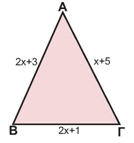
Το τρίγωνο ΑΒΓ έχει μήκη πλευρών 2χ+1, 2χ+3, χ+5.
Μπορείτε να βρείτε τη τιμή του χ ώστε να είναι ισοσκελές με βάση
α) τη ΒΓ β) την ΑΒ γ) την ΑΓ
ΑΛΛΑΓΗ ΓΡΑΜΗΣ
Χ ΙV) AΣΚΗΣΗ – ΠΡΟΚΛΗΣΗ ΓΙΑ ΛΙΓΟΥΣ:
Ενα νόμισμα είναι ελατωματικό. Προσπάθησε να το βρεις με όσο το δυνατόν λιγότερες προσπάθειες ζυγίσματος όταν
α)Εχεις σύνολο 8 νομίσματα και το ελατωματικό είναι το ελαφρύτερο
β) 9 νομίσματα και το ελατωματικό είναι το βαρύτερο από τα υπόλοιπα
γ) 12 νομίσματα και το ελατωματικό είναι ελαφρύτερο ή βαρύτερο από όλα τα άλλα.
ΔΟΚΙΜΑΣTΕ ΕΔΩ
Η ΕΠΙΜΕΡΙΣΤΙΚΗ ΙΔΙΟΤΗΤΑ
Δημοσιευμένο στην κατηγορία Α΄ ΓΥΜΝΑΣΙΟΥ, ΑΛΓΕΒΡΑ, ΑΛΓΕΒΡΑ Α΄, Β΄ΓΥΜΝΑΣΙΟΥ στις 27 Σεπ 2011
Στο Γυμνάσιο διδασκόμαστε την επιμεριστική ιδιότητα από τα πρώτα μαθήματα της Αλγεβρας .
α * (β + γ)= α * β + α * γ
Ο καθηγητής – καθηγήτρια μας, επιμένει να τη μάθουμε καλά γιατί όπως λέει είναι βασική ιδιότητα. Στην ερώτηση αν τη χρησιμοποιούμε στη ζωή μας, στη καθημερινότητα μας ξαφνιαζόμαστε, κοιταζόμαστε και απαντάμε πως μαλλον όχι, όχι δεν τη χρησιμοποιούμε. Και τότε γιατί να τη μαθαίνουμε; Που άραγε θα μας χρειαστεί; Ισως κάποιος επιστήμονας τη χρησιμοποιεί; …. Ε! σίγουρα θα τη χρειαστούμε κάπου στα …..μαθηματικά μας, για να το λέει ο καθηγητής – καθηγήτρια μας κάτι θα ξέρει …..
Η καθηγήτρια μας, μας ρώτησε να της εξηγήσουμε τι εννοούμε με τη φράση “νόστιμα και κατακόκκινα μήλα” , απαντήσαμε “νόστιμα μήλα και κατακόκκινα μήλα” και μετά μας ρώτησε πως αλλοιώς λέμε τη φράση “νόστιμα μήλα και νόστιμα αχλάδια” δώσαμε απάντηση “νόστιμα μήλα και αχλάδια”. Γράψαμε τις ισοδύναμες προτάσεις στον πίνακα κάτω από την επιμεριστική ιδιότητα και ξαφνικά παρατηρήσαμε μια ευθεία αντιστοιχία της επιμεριστικής ιδιότητας με το γλωσσικό πρότυπο!!!
Στη συνέχεια ζήτησε να της πούμε απλές ερωτήσεις / προβλήματα που απαντούσαμε / λύναμε στο Δημοτικό και πολλά από αυτά μας βοήθησε να τα συνδέσουμε με την επιμεριστική ιδιότητα. Θέλετε να σας τα πούμε κι εσάς;
- Στο δημοτικό από την πρώτη τάξη ο δάσκαλος /η δασκάλα, μας έμαθε ότι μπορούμε να προσθέτουμε μόνον όμοια πράγματα πχ:
Δηλαδή 3 μήλα + 2 μήλα = 5 μήλα
και με άλλο τρόπο λέγαμε:
3φορές![]() +2φορές
+2φορές ![]() = (3+2)φορές
= (3+2)φορές ![]() =5
=5 ![]()
3 μήλα + 2 μήλα = ( 3 + 2 ) μήλα = 5 μήλα
ΕΠΙΜΕΡΙΣΤΙΚΗ ΙΔΙΟΤΗΤΑ!
- Στην επόμενη τάξη μάθαμε να προσθέτουμε διψήφιους αριθμούς π.χ το 14 με το 53. Γράφαμε 14+53=67 και το βρίσκαμε με το μυαλό αφού αναλύαμε κάθε αριθμό στις δεκάδες Δ και τις μονάδες Μ που έχει και στη συνέχεια προσθέταμε μονάδες με μονάδες και δεκάδες με δεκάδες. Στο παράδειγμα μας ο 14=1Δ +4Μ και ο 53=5Δ +3Μ, οπότε
14+53=(1Δ+5Δ)+( 4Μ+3Μ)=(1+5) Δ+(4+3) Μ=6Δ+ 7Μ=67
ΕΠΙΜΕΡΙΣΤΙΚΗ ΙΔΙΟΤΗΤΑ!
- Σε άλλη τάξη μάθαμε διάφορα γεωμετρικά σχήματα και υπολογίζαμε την περίμετρο τους πχ την ημιπερίμετρο ενός ορθογωνίου παραλληλογράμμου με διαστάσεις 3,6 μ και 4 μ . Απαντούσαμε ότι η ημιπερίμετρος:
Η=3,6μ+ 4μ=7,6μ ή 3,6 μ + 4 μ =(3,6 + 4) μ = 7,6 μ
ΕΠΙΜΕΡΙΣΤΙΚΗ ΙΔΙΟΤΗΤΑ!
- Αργότερα μάθαμε να βρίσκουμε το εμβαδό ενός γεωμετρικού σχήματος π.χ το εμβαδό του παραπάνω ορθογωνίου είναι το γινόμενο των δύο διαστάσεων του 3,6 μ * 4 μ. Τον πολλαπλασιασμό αυτό τον κάναμε με δύο τρόπους α) κάναμε τη πράξη κατακόρυφα στο χαρτί μας 3,6 μ * 4 μ =14,4 τ.μ ή β) με το μυαλό μας. Θυμάμαι κάναμε ένα τέχνασμα για να το βρούμε με το μυαλό μας: γράφαμε τον αριθμό 3,6 =3 + 0.6 και μετά όλα ήταν εύκολα αφού 3* 4 =12 και 0,6 * 4 =2,4 Απαντούσαμε ότι το εμβαδό Ε, ισούται με το άθροισμα 12 + 2,4 = 14,4 τ.μ Δηλαδή λέγαμε
Ε=3,6μ *4μ =(3+0.6) *4 τ.μ =(3*4+ 0,6 *4 )τ.μ =(12 +2,4)τ.μ =14,4τ.μ ΠΑΛΙ ΚΑΙ ΠΑΛΙ Η ΕΠΙΜΕΡΙΣΤΙΚΗ ΙΔΙΟΤΗΤΑ!
-
 Ηθελα να ντύσω με αυτοκόλητο ντύμα ένα βιβλίο μου σε μέγεθος Α4 και ενα τετράδιο μου πιο κοντό σε μέγεθος. Με ρώτησε η μαμά πόσο αυτοκόλητο χρειαζόμουν για να αγοράσει. Για το βιβλίο μου μαζί με τα περιθώρια χρειαζόμουν αυτοκόλητο μήκους 32 εκ και για το τετράδιο 29 εκ. Η μαμά έκανε τη πράξη με το μυαλό της και μου είπε ότι θα αγοράσει αυτοκόλητο μήκους 61 εκ. Η μαμά είχε υπολογίσει :
Ηθελα να ντύσω με αυτοκόλητο ντύμα ένα βιβλίο μου σε μέγεθος Α4 και ενα τετράδιο μου πιο κοντό σε μέγεθος. Με ρώτησε η μαμά πόσο αυτοκόλητο χρειαζόμουν για να αγοράσει. Για το βιβλίο μου μαζί με τα περιθώρια χρειαζόμουν αυτοκόλητο μήκους 32 εκ και για το τετράδιο 29 εκ. Η μαμά έκανε τη πράξη με το μυαλό της και μου είπε ότι θα αγοράσει αυτοκόλητο μήκους 61 εκ. Η μαμά είχε υπολογίσει :
32 εκ + 29 εκ = (32+29) εκ = 61 εκ,
ΕΠΙΜΕΡΙΣΤΙΚΗ ΙΔΙΟΤΗΤΑ !
-
Αυτό το τέχνασμα μου άρεσε και το χρησιμοποιούσα αργότερα για να βρω το γινόμενο μεγάλων αριθμών ως εξής:
103*8 =(100+3)*8 =100*8+3*8 =800 +24=824
ΕΠΙΜΕΡΙΣΤΙΚΗ ΙΔΙΟΤΗΤΑ !
-
 Για τον υπολογισμό του μήκους υφάσματος που πρέπει να αγοράσω, για να μου ράψει η μοδίστρα δύο φούστες μια κοντή και μια μακρια ποια ιδιότητα των μαθηματικών χρησιμοποιώ;
Για τον υπολογισμό του μήκους υφάσματος που πρέπει να αγοράσω, για να μου ράψει η μοδίστρα δύο φούστες μια κοντή και μια μακρια ποια ιδιότητα των μαθηματικών χρησιμοποιώ;
ΤΗΝ ΕΠΙΜΕΡΙΣΤΙΚΗ ΙΔΙΟΤΗΤΑ !
-
Οταν λέω 3 χ+ 5 χ = ( 3 + 5 ) χ = 8 χ ποια ιδιότητα των μαθηματικών χρησιμοποιώ;
ΤΗΝ ΕΠΙΜΕΡΙΣΤΙΚΗ ΙΔΙΟΤΗΤΑ !
-
Ας δοκιμάσουμε να βρούμε με δύο τρόπους πόσα χρήματα θα μου κοστίσει το βάψιμο δύο τοίχων του δωματίου μου, αν το βάψιμο κάθε τετραγωνικού κοστίζει 2 ευρώ;ΕΔΩ–>

- Επιβεβαιώνουμε την ιδιότητα της επιμεριστικής ως προς την αφαίρεση και βρίσκουμε δικά μας παραδείγματα για τη χρησιμότητα της, στην καθημερινότητα μας.
α * (β – γ) = α * β – α * γ
Ενα περίεργο ταξίδι
Δημοσιευμένο στην κατηγορία Α΄ ΓΥΜΝΑΣΙΟΥ, ΑΛΓΕΒΡΑ, ΑΛΓΕΒΡΑ Α΄, Β΄ΓΥΜΝΑΣΙΟΥ, Γενικά, ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΔΙΑΣΚΕΔΑΣΗ στις 15 Μαρ 2011
ΑΠΟ ΤΟ ΑΠΕΙΡΟΕΛΑΧΙΣΤΟ ΣΤΟ ΑΠΕΙΡΟ.
Προπαίδεια δεκαδικών αριθμών
Δημοσιευμένο στην κατηγορία ΑΛΓΕΒΡΑ, Β΄ΓΥΜΝΑΣΙΟΥ στις 21 Φεβ 2011