26 Μάι 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
ΥΛΗ ΜΑΘΗΜΑΤΙΚΩΝ – ΜΑΙΟΣ 2012
25 Μάι 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Β΄ Τάξη Γυμνασίου
Μ Α Θ Η Μ Α Τ Ι Κ Α
Εξεταστέα ύλη διδακτικού έτους 2011 -2012
ΜΕΡΟΣ Α΄
Κεφ. 1ο: ΕΞΙΣΩΣΕΙΣ – ΑΝΙΣΩΣΕΙΣ
1.2 Εξισώσεις α’ βαθμού
1.4 Επίλυση προβλημάτων με τη χρήση εξισώσεων
1.5 Ανισώσεις α’ βαθμού
Κεφ. 2ο: ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ
2.1 Τετραγωνική ρίζα θετικού αριθμού
Κεφ. 4ο: ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ
4.1 Βασικές έννοιες της Στατιστικής : Πληθυσμός – Δείγμα
4.2 Γραφικές Παραστάσεις
4.3 Κατανομή συχνοτήτων και σχετικών συχνοτήτων
4.5 Μέση τιμή – Διάμεσος (χωρίς την υποπαράγραφο: «Μέση τιμή ομαδοποιημένης κατανομής»)
ΜΕΡΟΣ Β΄
Κεφ. 1ο: ΕΜΒΑΔΑ ΕΠΙΠΕΔΩΝ ΣΧΗΜΑΤΩΝ – ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ
1.3 Εμβαδά επίπεδων σχημάτων
1.4 Πυθαγόρειο θεώρημα
Κεφ. 2ο: ΤΡΙΓΩΝΟΜΕΤΡΙΑ
2.1 Εφαπτομένη οξείας γωνίας
2.2 Ημίτονο και συνημίτονο οξείας γωνίας
2.4 Οι τριγωνομετρικοί αριθμοί των γωνιών 30 , 45 και 60 μοιρών
Κεφ. 3ο: ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ
3.1 Εγγεγραμμένες γωνίες
3.2 Κανονικά πολύγωνα
3.3 Μήκος κύκλου
3.5 Εμβαδόν κυκλικού δίσκου
Καλή επιτυχία!
αα
2.1 Εφαπτομένη οξείας γωνίας
2.2 Ημίτονο και συνημίτονο οξείας γωνίας
2.4 Οι τριγωνομετρικοί αριθμοί των γωνιών 30 , 45 και 60 μοιρών
3.1 Εγγεγραμμένες γωνίες
3.2 Κανονικά πολύγωνα
3.3 Μήκος κύκλου
3.5 Εμβαδόν κυκλικού δίσκου
Α΄ Τάξη Γυμνασίου
Μ Α Θ Η Μ Α Τ Ι Κ Α
Εξεταστέα ύλη διδακτικού έτους 2011 – 2012
ΜΕΡΟΣ Α΄
Κεφ. 1ο: Οι φυσικοί αριθμοί
1.3 Δυνάμεις φυσικών αριθμών
1.4 Ευκλείδεια διαίρεση – Διαιρετότητα
1.5 Χαρακτήρες διαιρετότητας – Μ.Κ.Δ. – Ε.Κ.Π. – Ανάλυση αριθμού σε γινόμενο πρώτων παραγόντων
Κεφ. 2ο: Τα κλάσματα
2.1 Η έννοια του κλάσματος
2.2 Ισοδύναμα κλάσματα
2.3 Σύγκριση κλασμάτων
2.4 Πρόσθεση και Αφαίρεση κλασμάτων
2.5 Πολλαπλασιασμός κλασμάτων
2.6 Διαίρεση κλασμάτων
Κεφ. 4ο: Εξισώσεις και προβλήματα
4.1 Η έννοια της εξίσωσης – Οι εξισώσεις: α + χ = β, χ – α = β, α – χ = β,
α . χ = β, α : χ = β και χ : α = β
Κεφ. 5ο: Ποσοστά
5.1 Ποσοστά
5.2 Προβλήματα με ποσοστά
Κεφ. 6ο: Ανάλογα ποσά – Αντιστρόφως ανάλογα ποσά
6.1 Παράσταση σημείων στο επίπεδο
6.2 Λόγος δύο αριθμών – Αναλογία
6.3 Ανάλογα ποσά – Ιδιότητες αναλόγων ποσών
6.4 Γραφική παράσταση σχέσης αναλογίας
6.5 Προβλήματα αναλογιών
6.6 Αντιστρόφως ανάλογα ποσά
ΜΕΡΟΣ Β΄
Κεφ. 1ο: Βασικές γεωμετρικές έννοιες
1.7 Εφεξής και διαδοχικές γωνίες – Άθροισμα γωνιών
1.8 Παραπληρωματικές και Συμπληρωματικές γωνίες – Κατακορυφήν γωνίες
1.9 Θέσεις ευθειών στο επίπεδο
1.10 Απόσταση σημείου από ευθεία – Απόσταση παραλλήλων
1.11 Κύκλος και στοιχεία του κύκλου
1.13 Θέσεις ευθείας και κύκλου
Κεφ. 2ο: Συμμετρία
2.1 Συμμετρία ως προς άξονα
2.2 Άξονας συμμετρίας
2.3 Μεσοκάθετος ευθυγράμμου τμήματος
2.4 Συμμετρία ως προς σημείο
2.5 Κέντρο συμμετρίας
2.6 Παράλληλες ευθείες που τέμνονται από μία άλλη ευθεία
ΚΑΛΗ ΕΠΙΤΥΧΙΑ!!!
Πρωτομαγιά
2 Μάι 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Καλή πρωτομαγιά !
Με εργασία και χαρά!!!
Απο τη συλλογή μου: στεφάνι με κουβαρίστρες, σε βιτρίνα καταστήματος ειδών ραπτικής στη Ζάκυνθο!
Κανονικά πολύγωνα
28 Απρ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Κανονικά πολύγωνα γύρω μου
θέλετε να το διερευνήσετε;
πατήστε ΕΔΩ και χαρήτε την ιστοεξερεύνηση σας.
Προγραμματισμός των ρομπότ
10 Απρ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
“Σήμερα η μέρα ήταν φανταστική! Περάσαμε πολύ ωραία και γελάσαμε. Μάθαμε να προγραμματίζουμε το ρομπότ μας και φτιάξαμε ένα αστείο πρόγραμμα”!
Επι τέλους, καταφέραμε να κινήσουμε το ρομπότ και όχι μόνον! Είδαμε ότι στη κατασκευή μας οι θύρες B και C συνδέονται με τον δεξιό και αριστερό κινητήρα αντίστοιχα. Καταλάβαμε ότι το ρομπότ θα μπορούσε να κάνει οτιδήποτε θέλουμε, αρκεί να του δώσουμε τις κατάλληλες οδηγίες – εντολές. Μάθαμε να χρησιμοποιούμε αρκετά εργαλεία – εντολές του προγράμματος Mindstorms NXT, για το σκοπό αυτό. Προγραμματίσαμε στον υπολογιστή απλές λειτουργίες του ρομπότ όπως να κινείται, σε ευθεία, να στρίβει να σταματάει. Ενα εμπόδιο που είχαμε στο προγραμματισμό, το ξεπεράσαμε μόλις βρήκαμε την εντολή κίνησης Unlimited, δηλαδή συνεχούς κίνησης.
Συνδέσαμε το ρομπότ με τον υπολογιστή και κατεβάσαμε σε αυτό το πρόγραμμα μας. Πατούσαμε το κουμπί του ρομπότ για την εκτέλεση του προγράμματος και βλέπαμε τις κινήσεις του σε σχέση με αυτές που θέλαμε. Βελτιώναμε το πρόγραμμα συνεχώς και τελικά πετύχαμε το ρομπότ να κινείται με μέτρια ταχύτητα, να προχωρεί για λίγο μπροστά, να φρενάρει, να στρίβει αργά δεξιά, να μετακινείται αργά πίσω, να σταματάει απότομα και να μένει ακίνητο.
Περιηγηθήκαμε το βασικό μενού του ΝΧΤ και μάθαμε ότι ο προγραμματισμός μίας ρομποτικής μηχανής στηρίζεται συχνά στις τιμές (values) που συλλέγουν οι αισθητήρες της μηχανής από το περιβάλλον. Χρησιμοποιώντας το μενού View του ΝΧΤ, μπορούμε να δούμε τις τιμές που επιστρέφει κάθε αισθητήρας στον μικροεπεξεργαστή ΝΧΤ. Ασχοληθήκαμε με τον αισθητήρα φωτός για να δούμε αν το ρομπότ βλέπει. Ο αισθητήρας φωτός εκπέμπει φως και μετρά το ποσό του φωτός που ανακλάται. Έτσι μπορεί να διακρίνει επιφάνειες που απορροφούν το φως με διαφορετικό τρόπο. Συνδέσαμε τον αισθητήρα φωτός στην θύρα 3 (port 3) του ΝΧΤ, επιλέξαμε στο μενού View, τον αισθητήρα φωτός, τον αισθητήρα που μετρά το ανακλώμενο φως Reflected light και τη θύρα στην οποία έχει συνδεθεί ο αισθητήρα (Port 3).
Στην οθόνη είδαμε να αναγράφεται το ποσοστό του φωτός που ανακλάται. Μετακινήσαμε τον αισθητήρα πάνω σε διαφορετικά χρώματα και σημειώσαμε τις ενδείξεις του. Για τα ανοικτά χρώματα οι ενδείξεις ήταν μεγάλα νούμερα ενώ για τα σκούρα μικρά. Για το ίδιο αντικείμενο είχαμε διαφορετικές ενδείξεις ανάλογα με το πόσο φως το φώτιζε. Βλέπαμε μια ένδειξη όταν το είχαμε στο φως και τελείως διαφορετική όταν το είχαμε κάτω από το θρανίο! Αρα το ρομποτ ξεχωρίζει τα χρώματα; ΟΧΙ! “βλέπει” σε κλίμακα του γκρι ανάλογα με τη ποσότητα του ανακλώμενου φωτός!
Στη συνέχεια προσπαθήσαμε να δώσουμε την εντολή στο ρομπότ να κινείται σε μια περιοχή ανοικτόχρωμη και όταν “δει” σκούρο χρώμα να σταματήσει. Δυσκολευτήκαμε να το καταφέρουμε γιατί εκείνη τη μέρα είχαμε συχνά εναλλαγές του φωτός, μια η μέρα ήταν ηλιόλουστη και μια συννεφιασμένη και επιπλέον με πολύ κόπο καταλάβαμε ότι χρησιμοποιούσαμε εσφαλμένα το κριτήριο της ανισότητας. Δεν μπορείτε να φανταστείτε όμως τη τρελή χαρά μας όταν το βρήκαμε!!! Θέλαμε να κινείται όσο αντιλαμβανόταν ανοικτόχρωμη περιοχή και γνωρίζαμε ότι εκεί οι ενδείξεις μας είναι μεγάλα νούμερα. Δίναμε εντολή να σταματήσει όταν η ένδειξη light >40 ενώ το πετύχαμε όταν αντιστρέψαμε την ανίσωση. Βέβαια αυτό θέλαμε! να σταματήσει όταν “δεί” σκούρα περιοχή δηλαδή όταν οι τιμές του ανακλώμενου φωτός είναι μικρότερες από 40!!!
Η ομάδα των “έμπειρων” έχει βάλει αρχικό στόχο να κινεί το ρομπότ σε ευθεία και μόλις αυτό αντιλαμβάνεται εμπόδιο να αλλάζει πορεία. Στη συνέχεια το οδηγεί μέσα σε λαβύρινθο και επιθυμεί το ρομπότ να βρει την έξοδο. Είναι όμως εύκολο να το πετύχει; Τα κατάφερε το ρομπότ;
Δείτε το βίντεο με τις προσπάθειες των παιδιών.
Επίσκεψη στο Ιδρυμα Ευγενίδου
9 Απρ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
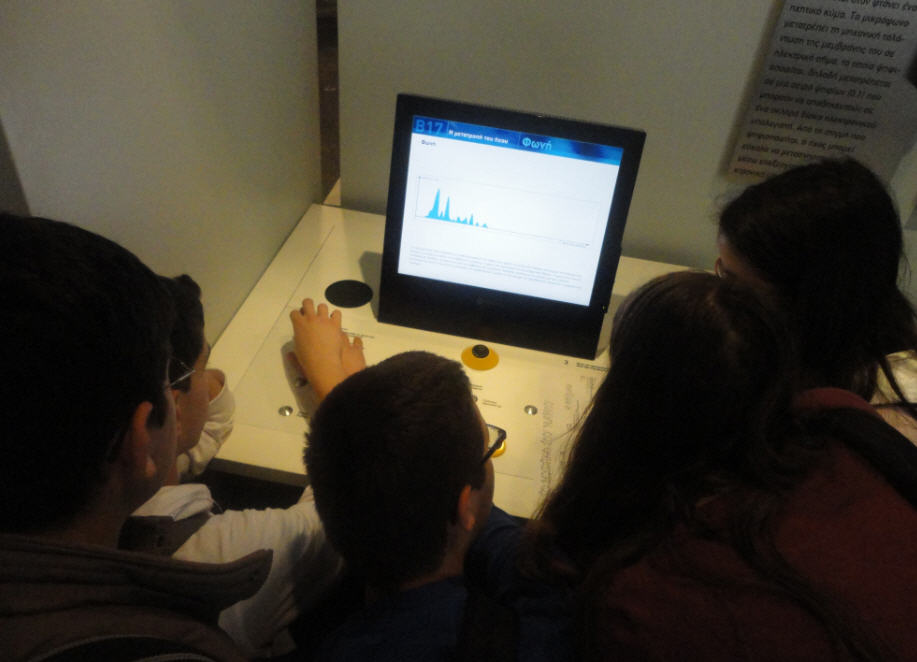
Η ομάδα μας, της Ρομποτικής, επισκέφθηκε τη διαδραστική έκθεση Επιστήμης και Τεχνολογίας, του Ιδρύματος Ευγενίδου. Ακολουθήσαμε τη διαδρομή: “Λύσε το μυστήριο”. Στους τρείς ορόφους του κτηρίου βρήκαμε και αξιοποιήσαμε εκθέματα με το απαραίτητο υλικό, για να λύσουμε τους γρίφους που μας δόθηκαν, στο γράμμα του Μάριου.
Το Μυστικό του Μάριου
Ο Μάριος είναι μεταπτυχιακός φοιτητής στο Πολυτεχνείο και βοηθά συχνά το θείο του τον Αριστοτέλη που είναι ιδιωτικός ερευνητής στην εξιχνίαση υποθέσεων. Μετά από μία σειρά απειλητικών τηλεφωνημάτων, ο Μάριος εξαφανίζεται. Λύσαμε λοιπόν μία σειρά γρίφων, προκειμένου να βοηθήσουμε το θείο Αριστοτέλη να ανακαλύψει τον ένοχο της απαγωγής.
Η όλη διαδικασία ήταν συναρπαστική! Μας έβαλε σε μια διαδικασία διερεύνησης των εκθεμάτων (πως λειτουργεί), κριτικής σκέψης (σχέση του εκθέματος με το ανάλογο ερώτημα του γρίφου), μάθησης μέσω παιχνιδιού και καλής συνεργασίας. Ανακαλύψαμε τις ιδιότητες σύνθετων υλικών, μάθαμε πώς λειτουργεί ένα τζάμι υγρών κρυστάλλων, ποια υλικά έχουν τη μεγαλύτερη αγωγιμότητα.
Επιπλέον μάθαμε πώς ακούει ο άνθρωπος και πώς γίνεται η ψηφιακή μετατροπή του ήχου. Γνωρίσαμε πώς το DNA επηρεάζει τα χαρακτηριστικά του κάθε ανθρώπου. Μάθαμε ότι μπορεί κανείς να μαθαίνει παίζοντας και να χαίρεται τη παρέα με τους συμμαθητές του.
Το DNA αποτελεί το γενετικό υλικό του ανθρώπου, που ευθύνεται για τη κληρονομικότητα. Περιέχει πληροφορίες απαραίτητες για τις λειτουργίες του οργανισμού, τα γονίδια. Αποτελείται από πολλά μόρια ενωμένα μεταξύ τους σε σχήμα αλυσίδας, μήκους περίπου 2 μέτρων.
Τα χρωμοσώματα είναι κομμάτια DNA τυλιγμένα σαν κουβάρι γύρω από πρωτείνες. Ο άνθρωπος έχει 46 χρωμοσώματα σε κάθε σωματικό του κύτταρο, τα οποία σχηματίζουν 23 ζευγάρια. Από αυτά τα 22 ζεύγη είναι μορφολογικά ίδια στα αρσενικά και τα θηλυκά άτομα και ονομάζονται αυτοσωμικά. Το 23ο ζευγάρι αποτελείται από τα φυλετικά χρωμοσώματα που συμβολίζονται με Χ και Y. Τα κύταρα των θηλυκών ατόμων περιέχουν δύο χρωμοσώματα Χ ενώ των αρσενικων ένα Χ και ένα Y. Η ταξινόμηση των χρωμοσωμάτων σύμφωνα με το μέγεθος και το σχήμα λέγεται ΚΑΡΥΟΤΥΠΟΣ. Ετσι λέμε ότι ο καρυότυπος ενός αρσενικού ατόμου είναι 46,XY ενώ του θηλυκού 46,ΧΧ
Δοκιμάστε να ταιριάξετε τα χρωμοσώματα και να σας αποκαλυφθεί ο καρυότυπος ενός ατόμου. Προσπαθήστε σύροντας τα χρωμοσώματα από τα αριστερά να τα ταιριάξετε με το ζευγάρι τους δεξιά, στη παρακάτω εφαρμογή.
Τι συμβαίνει όταν υπάρχουν περισσότερα ή λιγότερα χρωμοσώματα στον καρυότυπο; Οταν ένα χρωμόσωμα έχει χάσει ένα του κομμάτι;
Οι μαθητές συνήθως υποστηρίζουν ότι τα κορίτσια κληρονομούν τα χαρακτηριστικά τους από τη μητέρα, ενώ τα αγόρια από τον πατέρα ή το αντίστροφο. Ποια είναι η αλήθεια; Τι είναι δαλτωνισμός και πως προκύπτει αυτό; Δημιουργείστε μια οικογενειακή φωτογραφία .
Μπορώ να δω το δικό μου DNA; με 4 βήματα στο σπίτι.
Οι συνοδοί καθηγητές μας: Μήτσιου Αρετή, Ελευθερίου Λάμπρος , Αρδαβάνη Πόπη.
Κ Α Λ Ο Π Α Σ Χ Α!
8 Απρ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
ΠΑΣΧΑΛΙΝΕΣ ΚΑΡΤΕΣ
6 Απρ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
ΕΥΧΕΣ ΜΕ “ΕΞΥΠΝΕΣ” ΚΑΡΤΕΣ
Αν θέλετε να φτιάξετε “έξυπνες” κάρτες, κάρτες που “λένε” ατέλειωτες ιστορίες ακολουθήστε τα παρακάτω:
1)Παίρνετε ένα χαρτόνι κανσόν μεγέθους Α4
2)Κόβετε ένα ορθογώνιο με διαστάσεις της αρεσκείας σας (μέγεθος κάρτας). Προτεινόμενες διαστάσεις 8cm x 12cm
ααααα
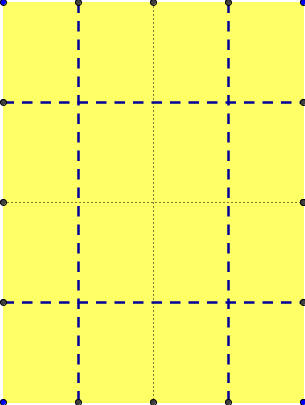
3)Με γεωμετρικά όργανα, μολύβι, τρίγωνο, χάρακα χαράζετε τρεις παράλληλες και τρεις κατακόρυφες με διακεκομμένες ευθείες, ώστε να χωρίζεται η κάρτα σε ίσα ορθογώνια. Σύμφωνα με τις προτεινόμενες διαστάσεις τα μικρά τμήματα είναι 2cm και τα μεγαλύτερα 3cm.
4)Τσακίζετε καλά την κάρτα πάνω στις εξωτερικές ευθείες.
5)Με το ψαλίδι κόβετε προσεκτικά κατα μήκος των διαγωνίων του εσωτερικού ορθογωνίου.Μια καλή ιδέα είναι να διπλώσουμε τη κάρτα στη μέση και μετά να κόψουμε με το ψαλίδι το σχήμα “ν” που βλέπουμε.
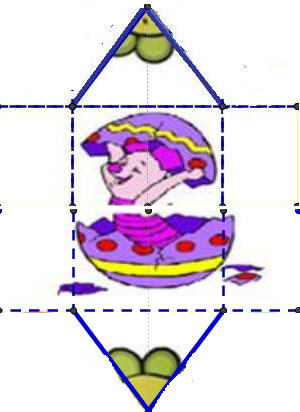
6)Ζωγραφίζετε τα δικά σας σχέδια ή κολλάτε αυτοκόλητα με προσοχή και αφαιρετική σκέψη, ώστε η κάρτα σας να “λέει” μετά πολλές ιστορίες. Εναλλακτικά μπορείτε πρώτα να διπλώνετε κατάλληλα τη κάρτα σας και τότε να σχεδιάζετε τις δικές σας ιστορίες, ώστε να διαβάζονται σωστά μετά.
ααααα
7)Αρχίστε το “διάβασμα” της κάρτας.”Βλέπετε ένα γουρουνάκι να βγαίνει μέσα από ένα αυγό κότας; Μήπως όμως τελικά βγήκε από ένα σοκολατένιο αυγό;
Καλές αναγνώσεις!
Μερικά ερωτήματα:
1)Το ορθογώνιο στη πορεία του διαβάσματος της κάρτας τι μορφές πήρε;
2)Τα μέρη των διαγωνίων του εσωτερικού ορθογωνίου, τι σχέση έχουν με τις πλευρές του ρόμβου που σχηματίζεται κάποια στιγμή;
3)Παρατηρήστε ένα ακόμη ορθογώνιο μέσα στον ρόμβο. Τι σχέση έχει με το αρχικό εσωτερικό ορθογώνιο;
ααα
Μερικές δημιουργίες μαθητών:
Δοκιμάστε να εκτυπώσετε το έγγραφο .zip και στις δύο του όψεις ώστε να έχετε ευχετήριες κάρτες πασχαλινές.
ΚΑΛΟ ΠΑΣΧΑ!!!
ααα
Και η Μ ε γ ά λ η ααα έ κ π λ η ξ η !!!
Μετά το Πάσχα έφεραν αρκετοί μαθητές τις δικές τους κάρτες. Ας τις δούμε:
Συμμετρία
5 Απρ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
ΕΡΓΑ ΜΑΘΗΤΩΝ
Μετά την ολοκλήρωση των μαθημάτων της συμμετρίας ως προς άξονα και ως προς σημείο, οι μαθητές επανέρχονται με νέες ιδέες και δημιουργίες. Καμαρώστε την έμπνευση τους και τη δουλειά τους:
aaa
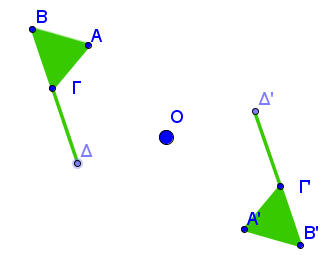
Συμμετρία ως προς σημείο
5 Απρ 2012 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
My counter
Κατηγοριες
Σελίδες
Ετικέτες
fractals games geogebra illusion illusions lego mindstorms NXT Sierpinski symmetry Πείραμα του Ερατοσθένη Πυθαγόρειο Πυθαγόρειο θεώρημα Χριστουγεννα Χριστουγεννιάτικες ευχές άξονες συμμετρίας ίσα τρίγωνα αντίστροφο πυθαγορείου αυτοαξιολόγηση δημιουργίες μαθητών εμβαδό εμπλουτισμένα βιβλία εξίσωση εξεταστέα ύλη εξισώσεις πρώτου βαθμού ευχές ισοδύναμα σχήματα καινοτόμα μαθήματα κανονικά πολύγωνα κατασκευές μαθητών μαθηματικά και τέχνη μαθηματικά παιχνίδια μοτίβα μοτίβο ομαδοσυνεργασία οφθαλμαπάτες οφθαλμαπάτη παιχνίδι πασχαλινά αυγά πασχαλινές ευχές προοπτική ρομποτική συμμετρία ως προς άξονα συμμετρια σχολικά βιβλίαΣΕΛΙΔΕΣ
Blogroll
Μεταστοιχεία
-