Υποθέτουμε ότι έχουμε ένα ισόπλευρο τρίγωνο ΑΒΓ.
Βρίσκουμε τα μέσα των πλευρών του και σχηματίζουμε τα τέσσερα ισόπλευρα τρίγωνα από τα οποία αφαιρούμε το μεσαίο.Εχουμε το βασικό μοτίβο, σχήμα 1.
Συνεχίζουμε την ίδια διαδικασία στα τρίγωνα που εναπομένουν.
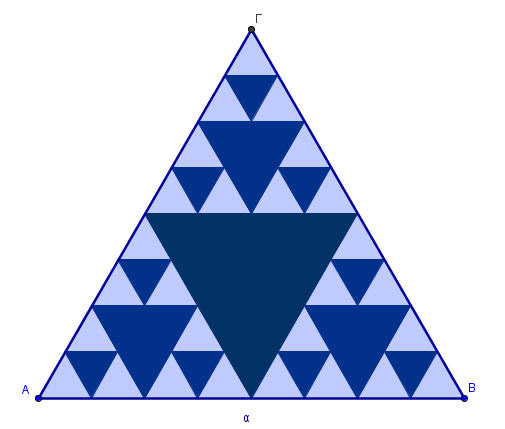
Αν επαναλάβουμε τη διαδικασία πάρα πολλές φορές το τρίγωνο που δημιουργείται ονομάζεται τρίγωνο του Sierpinski.
Είναι ενδιαφέρον να υπολογίσουμε τη περίμετρο και το εμβαδό αυτού του τριγώνου.Για ν επαναλήψεις, όπου ν μεγάλος αριθμός, το εμβαδό του τείνει να γίνει 0 τ.μ, ενώ η περίμετρος του τείνει στο άπειρο. Ας δοκιμάσουμε πατώντας πάνω στην εικόνα που ακολουθεί.
Ας δούμε ένα άλλο τρίγωνο, το τρίγωνο Pascal .
Πιστεύετε ότι έχει κάποια σχέση με το τρίγωνο του Sierpinski ;
Οι αριθμοί Fibonacci 1,1, 2, 3, 5, 8, 13, 21,…
προκύπτουν ως εξής: 1, 1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, ….
Πιστεύετε ότι έχουν σχέση με το τρίγωνο του Pascal;





Αφήστε μια απάντηση
Για να σχολιάσετε πρέπει να συνδεθείτε.