Το βίντεο που δημοσιεύουμε με τον παραπάνω τίτλο, είναι επανεγγραφή του αντιστοίχου μαθήματος, με ίδιο περιεχόμενο που δημοσιεύσαμε πριν 4 χρόνια, αλλά με τη χρήση του νέου περιβάλλοντος του προγράμματος.

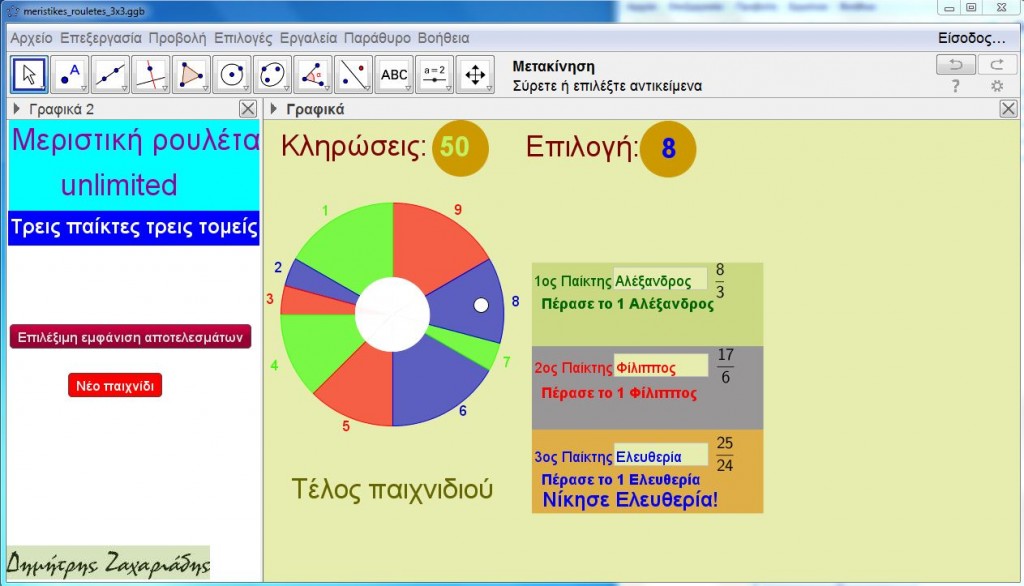
Μεριστικές Ρουλέτες

Για τη διδασκαλία των κλασμάτων στο Δημοτικό και στο Γυμνάσιο έχουν, κατά κόρον ίσως, χρησιμοποιηθεί μοντέλα με βάση το εμβαδόν, όπως κυκλικές τούρτες, πίτες και πίτσες. Τα μοντέλα αυτά αν και αρκετά παραστατικά είναι στατικά, δηλαδή δεν έχουν δυναμικό χαρακτήρα.

Οι μεριστικές ρουλέτες είναι ένα παιχνίδι, όπου οι παίκτες μοιράζονται τα κομμάτια μιας “πίτας” ιδιόρρυθμης και δυναμικής: τα κομμάτια της δεν είναι ίσα και γίνεται διαρκώς κλήρωση (η “πίτα” μετατρέπεται σε “ρουλέτα”). Σκοπός δεν είναι οι παίκτες να κερδίσουν χρήματα, αλλά να κατακτήσουν αυτοδύναμη γνώση για τα κλάσματα, τις γεωμετρικές αναπαραστάσεις τους και να δώσουν ένα νόημα στην πρόσθεση κλασμάτων μέσα από μια συναρπαστική εμπειρία παιχνιδιού, όπου θα μπορούν να αλλάζουν και μέρος των κανόνων έτσι στη διαδικασία της μάθησής τους. Μια τέτοια βιωματική εμπειρία προκαλεί περισσότερο τη σύμπραξη και την ανταλλαγή ιδεών και εμπειριών, παρά τον ανταγωνισμό με σκοπό την εύνοια του δασκάλου προς τους μαθητές που τα “καταφέρνουν” καλύτερα.

Στο συνέδριο της Ελληνικής Μαθηματικής Εταιρείας, που έγινε στην Βέροια τον Νοέμβριο του 2014, είχαμε παρουσιάσει εγώ και ο Επίκουρος καθηγητής του Μαθηματικού Τμήματος Τάσος Πατρώνης εισήγηση με θέμα:

Μεριστικές Ρουλέτες: Αλλάζουμε το παιχνίδι για να συμμετάσχουμε στο σχέδιο της μάθησης μας.

Πρακτικές και καινοτομίες στην εκπαίδευση και στην έρευνα

Στο συνέδριο αυτό παρουσίασα την ψηφιακή έκδοση του παιχνιδιού.

Η σημερινή δημοσίευση περιλαμβάνει δύο αρχεία Geogebra, το παιχνίδι σε δύο εκδοχές, η πρώτη για δύο παίχτες (τρεις περιπτώσεις) και η δεύτερη για τρεις παίκτες καθώς και αντίγραφο της εισήγησης του Συνεδρίου που αναφέρω πιο πάνω, όπου υπάρχει όλο το σκεπτικό του παιχνιδιού.

Για να κατεβάσετε τα αρχεία πατήστε επάνω στην εικόνα.

Δημήτρης Ζαχαριάδης

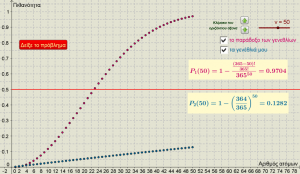
Το παράδοξο των γενεθλίων στη θεωρία πιθανοτήτων αναφέρεται σε ένα πρόβλημα το οποίο, κατά την κοινή λογική, έχει μια απίθανη απάντηση. Μία από τις μορφές του προβλήματος είναι: “σε μία ομάδα 23 ατόμων τι πιθανότητα υπάρχει δύο από αυτά τα άτομα να έχουν την ίδια ημέρα γενέθλια”; Η “πιθανά προφανής” απάντηση είναι 23/365=0,063 δηλαδή έξι τοις εκατό. Η μαθηματική λύση όμως μας δίνει 50%! Ακόμα πιο εντυπωσιακά, το ποσοστό γίνεται 99% με μόνο 57 άτομα! Στην εφαρμογή που αναρτούμε υπολογίζεται η πιθανότητα αυτή για διαφορετικά πλήθη ατόμων. Επίσης, υπολογίζεται και η πιθανότητα ύπαρξης της ίδιας μέρας γενεθλίων με συγκεκριμένο άτομο της ομάδας, ανεξάρτητα ή και σε αντιδιαστολή με την προηγούμενη πιθανότητα.

Θα μπορούσε να διδαχθεί στο μάθημα των πιθανοτήτων τόσο στην Α’ Λυκείου, όσο και στα Μαθηματικά Γενικής Παιδείας στη Γ’ Λυκείου.

Για να μεταφορτώσετε την εφαρμογή πιέστε επάνω στην εικόνα.

Oι εξισώσεις για τις οποίες είναι γνωστή η αναλυτική λύση είναι πολύ λιγότερες από αυτές στις οποίες η αναλυτική λύση δεν είναι γνωστή. Για παράδειγμα για την εξίσωση x + e^x = 0 δεν είναι γνωστή η αναλυτική λύση. Σε αυτήν την περίπτωση είναι δυνατή η επίλυση της εξίσωσης με αριθμητικές μεθόδους. Στο Λύκειο γίνεται μια αναφορά σε προσεγγιστική λύση εξίσωσης (πολυωνυμικής) στη Β’ Λυκείου, η οποία χωρίς τη χρήση υπολογιστή μένει μετέωρη… Εξάλλου η συγκεκριμένη μέθοδος βασίζεται στο θεώρημα του Bolzano που διδάσκεται την επόμενη χρονιά. Στην εφαρμογή που παρουσιάζουμε δίνουμε τη δυνατότητα αριθμητικής επίλυσης μιας εξίσωσης με τη μέθοδο της «Διχοτόμησης» και με τη μέθοδο «Newton-Raphson», που κατά τη γνώμη μας θα μπορούσαν να παρουσιαστούν στα Μαθηματικά Κατεύθυνσης της Γ’ Λυκείου, η πρώτη σαν εφαρμογή του θεωρήματος Bolzano, ενώ η δεύτερη σαν εφαρμογή των παραγώγων.

Εισάγουμε με αυτόν τον τρόπο τους μαθητές στην έννοια των αριθμητικών μεθόδων που εφαρμόζονται ευρέως στις θετικές επιστήμες.

Μπορείτε να μεταφορτώστε το αρχείο πατώντας πάνω στην εικόνα. Μπορείτε επίσης να μεταφορτώσετε ένα αρχείο εύρεσης ριζών εξίσωσης με τις δύο μεθόδους σε Mathematica 8.0 πατώντας εδώ.

Η εφαρμογή που παρουσιάζεται εδώ δίνει μια γραφική και αναλυτική λύση σε ένα κλασσικό πρόβλημα πιθανοτήτων που διατυπώνεται ως εξής:

«αν κόψουμε τυχαία ένα ευθύγραμμο τμήμα στα τρία, ποια η πιθανότητα αυτά τα τρία μέρη να  μπορούν να σχηματίσουν τρίγωνο;».

Η γραφική λύση χρησιμοποιεί δύο χαρακτηριστικές προτάσεις της Ευκλείδειας γεωμετρίας, μια από τις οποίες είναι  το θεώρημα του Viviani.

Για να μεταφορτώσετε την εφαρμογή πατήστε επάνω στην εικόνα.

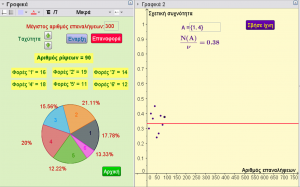
Στη θεωρία Πιθανοτήτων ο νόμος των μεγάλων αριθμών περιγράφει το αποτέλεσμα της επανάληψης ενός πειράματος τύχης. Σύμφωνα με το νόμο αυτό, ο μέσος όρος των αποτελεσμάτων που έχουν πραγματοποιηθεί σε διαδοχικές επαναλήψεις του πειράματος προσεγγίζει την αναμενόμενη τιμή (θεωρητική μέση τιμή) του πειράματος, όσο ο αριθμός των επαναλήψεων αυξάνει, Από αυτό προκύπτει ότι όταν το πλήθος των δοκιμών ενός πειράματος τύχης αυξάνει απεριόριστα, η σχετική συχνότητα ενός εκάστου ενδεχομένου προσεγγίζει τη θεωρητική του πιθανότητα. Η εφαρμογή που αναρτάται αναπαριστά το συγκεκριμένο νόμο στις περιπτώσεις του νομίσματος και του ζαριού. Ο χρήστης μπορεί να επιλέξει το συνολικό αριθμό ρίψεων καθώς επίσης και το ενδεχόμενο που σας ενδιαφέρει (στην περίπτωση του νομίσματος Κεφάλι ή Γράμματα, ενώ στην περίπτωση του ζαριού οποιοδήποτε απλό ή σύνθετο ενδεχόμενο).

Η εφαρμογή βασίζεται στην ακόλουθη ιδέα: δημιουργεί μια λίστα, μήκους ν₀ (που καθορίζεται από το χρήστη και παριστάνει το συνολικό αριθμό ρίψεων), τυχαίων αριθμών (στη περίπτωση του νομίσματος είναι {Κεφάλι ή Γράμματα} ενώ στην περίπτωση του ζαριού {1, 2, 3, 4, 5 ή 6}. Δημιουργείται, στη συνέχεια , ένας δρομέας ν που ανατρέχει τη λίστα που έχει δημιουργηθεί, ανά δέκα στοιχεία, και μετρά τον αριθμό των απλών ή σύνθετων (στην περίπτωση του ζαριού)  ενδεχομένων του πειράματος που έχουν προκύψει μέχρι την τρέχουσα τιμή του ν.

Θα μπορούσε να διδαχθεί στο μάθημα των πιθανοτήτων τόσο στην Α’, όσο και στα Μαθηματικά Γενικής Παιδείας στη Γ’ Λυκείου.

Για να μεταφορτώσετε την εφαρμογή πατήστε πάνω στην εικόνα.

Limnos 14_12_2015 Limnos 17_12_2015

Κατόπιν απόφασης του Περιφερειακού Διευθυντή Α/θμιας & Β/θμιας Εκπαίδευσης Βορείου Αιγαίου Αριστείδη Καλάργαλη και θετικής εισήγησης του Προϊστάμενου Επιστημονικής & Παιδαγωγικής Καθοδήγησης Β/θμιας Εκπ/σης Β. Αιγαίου κ. Πρόδρομου Ελευθερίου, διοργανώθηκε από το Σχολικό Σύμβουλο ΠΕ03 της Δ/νσης Β/θμιας Εκπ/σης Σάμου με αρμοδιότητα και στις περιοχές Ν. Χίου και Λέσβου κ. Ιωάννη Ράλλη, την 15^η Δεκεμβρίου 2015  στη Λήμνο,  επιμορφωτική συνάντηση με θέμα τη «Χρήση του λογισμικού Geogebra στη διδασκαλία των Μαθηματικών», στην οποία ήταν εισηγητής ο συνάδελφος και φίλος Δημήτρης Ζαχαριάδης.

Στο περιθώριο της συνάντησης αυτής, παρουσίασε δύο δειγματικές διδασκαλίες. Η πρώτη έγινε στις 14 Δεκεμβρίου, στη Β’ Λυκείου του Λυκείου Μούδρου, με θέμα τη μελέτη των τριγωνομετρικών συναρτήσεων και ιδιαίτερα μελέτη και γραφική παράσταση της συνάρτησης εφαπτομένη. Η δεύτερη έγινε στις 17 Δεκεμβρίου, στη Β’ Λυκείου του Λυκείου Μύρινας, με θέμα τη μελέτη των τριγωνομετρικών συναρτήσεων ημίτονο και συνημίτονο και μελέτη της συνάρτησης f(x)=ρημωx με ρ≠0 και ω>0

Μπορείτε να μεταφορτώσετε το υλικό της πρώτης δειγματικής διδασκαλίας πατώντας εδώ και της δεύτερης πατώντας εδώ.

Xios 20_11_2015

Το διήμερο 20  και 21 Νοεμβρίου 2015 ο συνάδελφος και φίλος Δημήτρης Ζαχαριάδης μετέβη στην Χίο, κατόπιν πρόσκλησης του Σχολικού Συμβούλου ΠΕ03 της Δ/νσης Β/θμιας Εκπ/σης Σάμου με αρμοδιότητα και στις περιοχές Ν. Χίου και Λέσβου κ. Ιωάννη Ράλλη και του τοπικού παραρτήματος της ΕΜΕ, ώστε να συμμετάσχει σε επιμορφωτική συνάντηση με θέμα τη «Χρήση του λογισμικού Geogebra στη διδασκαλία των Μαθηματικών». Στα πλαίσια της συνάντησης αυτής, την 20^η Νοεμβρίου παρουσίασε μια δειγματική διδασκαλία στη Β’ Λυκείου του 1^ου Λυκείου Χίου, με θέμα τη μελέτη και γραφική παράσταση της συνάρτησης ημίτονο. Η διδασκαλία έγινε σε Εργαστήριο Πληροφορικής με τους μαθητές να συμπληρώνουν το φύλλο εργασίας με τη βοήθεια εφαρμογών Geogebra που δημιουργήθηκαν γι’ αυτόν το σκοπό.  Μπορείτε να μεταφορτώσετε το υλικό της δειγματικής διδασκαλίας πατώντας στη φωτογραφία.

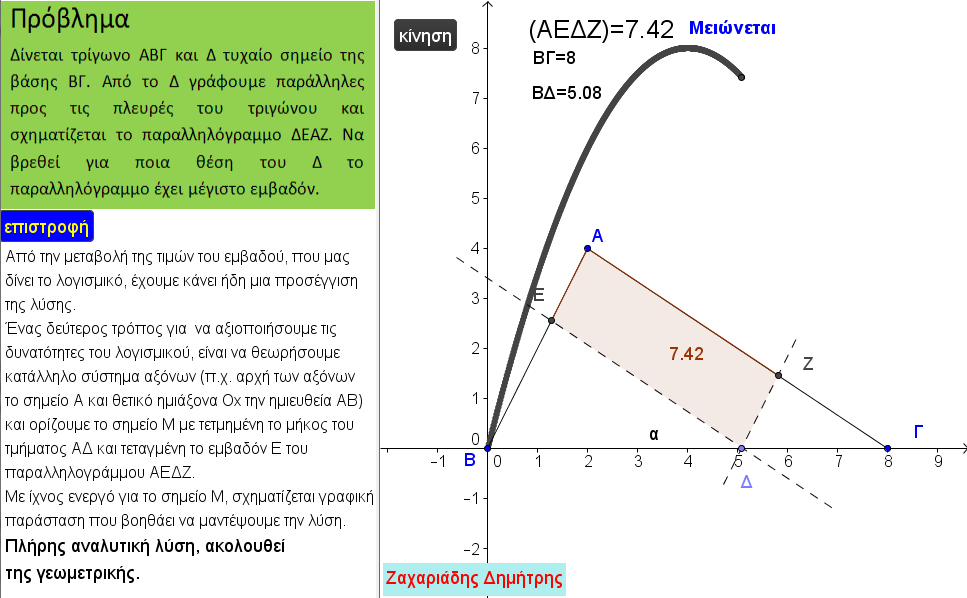
Η εφαρμογή που δημοσιεύουμε αφορά ένα πρόβλημα γεωμετρίας,  που αναφέρεται στον προσδιορισμό του μεγίστου εμβαδού ενός παραλληλογράμμου εγγεγραμμένου σε τρίγωνο.

Η εφαρμογή αυτή μπορεί να διδαχθεί στην Β΄ Λυκείου και γενικά στο  Λύκειο, κατά την κρίση του διδάσκοντος.

Με την βοήθεια του λογισμικού δίνεται η ευκαιρία στον μαθητή να μαντέψει ενορατικά την λύση και στην συνέχεια παρουσιάζονται με βήματα  λύσεις, γεωμετρική, αλγεβρική και αναλυτική και μπορούν να στηθούν πολλά σενάρια διδασκαλίας.

Παρουσιάζει μεγάλο διδακτικό ενδιαφέρον γιατί εμπλέκονται πολλές ενότητες από την ύλη των μαθηματικών όπως οι παρακάτω:

• Όμοια τρίγωνα
• Μετρικές σχέσεις εμβαδών τριγώνου
• Τριγωνομετρία
• Μετρικές σχέσεις ορθογωνίου τριγώνου.
• Μελέτη και γραφική παράσταση τριωνύμου
• Αλγεβρικές ταυτότητες.

Μπορείτε να δείτε το αρχείο on line κάνοντας κλικ επάνω στην εικόνα.

Για να κατεβάσετε το αρχείο κάντε κλικ   εδώ

Το βίντεο που δημοσιεύουμε με τον παραπάνω τίτλο, είναι επανεγγραφή του αντιστοίχου μαθήματος, με ίδιο περιεχόμενο που δημοσιεύσαμε πριν 4 χρόνια, αλλά με τη χρήση του νέου περιβάλλοντος του προγράμματος.