Άρθρα: ΔΙΔΑΣΚΑΛΙΕΣ
Δημοσιεύουμε αρχείο που δείχνει με βήματα την κατασκευή της χρυσής τομής του χρυσού ορθογώνιου και της χρυσής σπείρας.
Το ενδιαφέρον και η πρωτοτυπία του είναι η χρήση της εντολής ΛίσταΕπανάληψης για τον σχηματισμό λίστας σημείων που χρειάζονται για τον σχηματισμό της Χρυσής σπείρας. Με την χρήση αυτής της εντολής δεν χρειάζεται να δημιουργήσουμε ένα – ένα τα κομμάτια της κατασκευής αλλά μπορούμε να φθάσουμε απευθείας στο τελικό αποτέλεσμα.
Μαζί με το αρχείο Geogebra δημοσιεύουμε και ένα κείμενο με οδηγίες και παραδείγματα για την εντολή αυτή.
Για να κατεβάσετε το αρχείο Geogebra και το κείμενο με τις οδηγίες πατήστε εδώ.
 Δημοσιεύουμε μια παρουσίαση (ppt) που αφορά στον τρόπο μέτρησης του ύψους της πυραμίδας του Χέοπα από το Θαλή το Μιλήσιο. Ο βασικός κορμός της παρουσίασης βασίζεται στο βιβλίο του Denis Guedj “Το θεώρημα του παπαγάλου”.
Δημοσιεύουμε μια παρουσίαση (ppt) που αφορά στον τρόπο μέτρησης του ύψους της πυραμίδας του Χέοπα από το Θαλή το Μιλήσιο. Ο βασικός κορμός της παρουσίασης βασίζεται στο βιβλίο του Denis Guedj “Το θεώρημα του παπαγάλου”.
Απευθύνεται στους μαθητές της Γ’ Γυμνασίου και της Β’ Λυκείου που διδάσκονται το κεφάλαιο των Αναλογιών στη Γεωμετρία.
Για να κατεβάσετε την παρουσίαση πιέστε εδώ
Την Πέμπτη 25 Φεβρουαρίου έγινε επιμορφωτική συνάντηση των μαθηματικών Γυμνασίου του Βορείου Αιγαίου που διοργανώθηκε από τη συντονίστρια ΠΕ03 Καλφοπούλου Κατερίνα και που είχε θέμα «Προτάσεις για την διδασκαλία της γεωμετρίας στο γυμνάσιο στη δία ζώσης και στην εξ αποστάσεως εκπαίδευση». Στη συνάντηση αυτή παρουσιάστηκε αρχείο Geogebra “Στοιχειώδεις γεωμετρικές κατασκευές με ψηφιακά όργανα σχεδίασης» από το Δημήτρη Ζαχαριάδη επ. σχολικό σύμβουλο Μαθηματικών. Το αρχείο αυτό δίνει τη δυνατότητα στον εκπαιδευτικό να διδάξει, είτε εξ αποστάσεως , είτε δια ζώσης, τη χρήση των γεωμετρικών οργάνων (διαβήτη, μοιρογνωμόνιο γνώμονα κλπ) με τρόπο που προσομοιάζει τον χειραπτικό. Επισυνάπτεται το αρχείο αυτό και κείμενο με παραδείγματα στοιχειωδών κατασκευαστικών. Δράσεων.
Για να κατεβάσετε τα σχετικά αρχεία πατήστε εδώ.
Η παρούσα ανάρτηση αποτελεί εισήγησή στην 11η Μαθηματική Εβδομάδα (Διεθνές Συνέδριο που διοργανώνεται από το Παράρτημα της ΕΜΕ Θεσσαλονίκης) από τους τους Πατρώνη Τάσο, Επίκουρο Καθηγητή Τμ. Μαθηματικών Παν/μίου Πάτρας, Ζήση Μαρία, καθηγήτρια του 2ου Γυμνασίου Μυτιλήνης και εμένα με τίτλο: «Διδασκαλία της Άλγεβρας της Γ΄ Γυμνασίου με γεωμετρική μορφή των αλγεβρικών παραστάσεων και με την βοήθεια ειδικού αρχείου – εφαρμογής Geogebra».
Πρόκειται για μια πρόταση διδασκαλίας των ενοτήτων πράξεις πολυωνύμων, τις ταυτότητες και την παραγοντοποίηση της ύλης της Γ’ Γυμνασίου, που εφαρμόστηκε στο 2ο Γυμνάσιο Μυτιλήνης όπου συνδυάστηκαν χειραπτικό υλικό με εφαρμογή του λογισμικού Geogebra.
Σημαντική διαφορά με παρόμοιες διδακτικές προτάσεις είναι ότι η επικάλυψη ενός σχήματος με ορθογώνια και τετράγωνα παριστάνει ένα άθροισμα μονωνύμων, ενώ για την διαφορά δύο μονωνύμων ή πολυωνύμων χρησιμοποιείται απλώς η αποκοπή.
Το πλεονέκτημα αυτής της μεθόδου είναι ότι οι μαθητές δημιουργούν εικόνες για τις αφηρημένες αυτές έννοιες της άλγεβρας έτσι αυτές αποκτούν ένα πιο συγκεκριμένο νόημα γι αυτούς αντί να τις μαθαίνουν μηχανικά όπως συνήθως. Έτσι ο μαθητής πείθεται για την αλήθεια των όσων πραγματεύεται η άλγεβρα και δεν την θεωρεί ένα παιχνίδι συμβόλων.
Δημοσιεύουμε εδώ:
-
την εισήγηση
-
τα σχετικά αρχεία Geogebra και
-
τα φύλλα εργασίας των δύο διδασκαλιών
Για να κατεβάσετε τα αρχεία πατήστε εδώ.
Δημήτρης Ζαχαριάδης
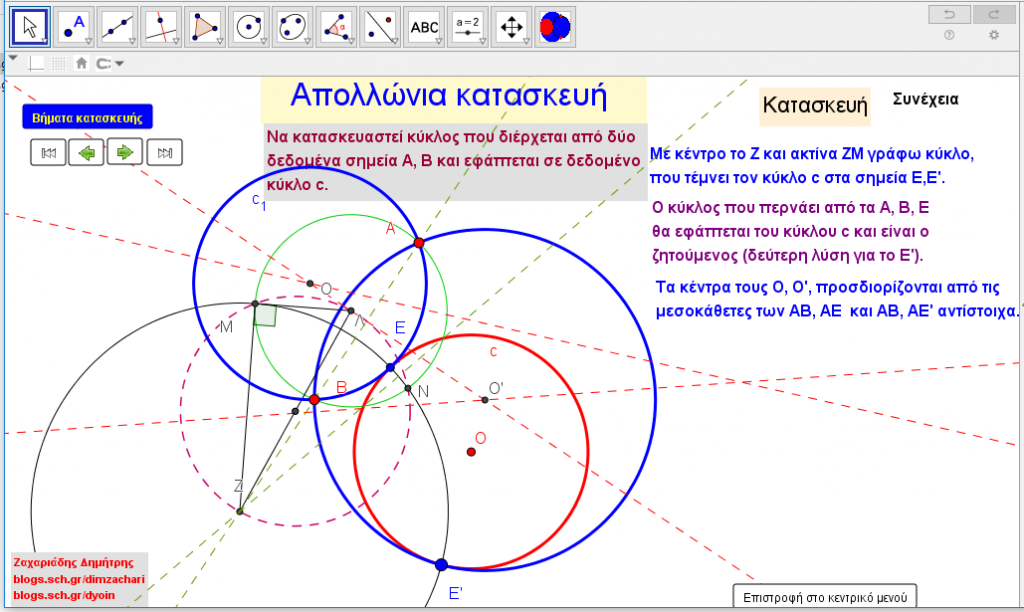
Η δημοσίευση αυτή είναι η τρίτη με τον ίδιο γενικό τίτλο, «Απολλώνιο Πρόβλημα».
Το Απολλώνιο Πρόβλημα «να γραφεί κύκλος που να εφάπτεται σε τρεις δεδομένους κύκλους», λυμένο από τον μεγάλο μαθηματικό της αρχαιότητας Απολλώνιο τον Περγαίο, είναι το κορυφαίο πρόβλημα, από μια σειρά επί μέρους προβλημάτων των οποίων η επίλυση οδηγεί σταδιακά στην λύση του.
Τα προβλήματα αυτά έχουν τη γενική διατύπωση: «Να γραφεί κύκλος που εφάπτεται σε τρία αντικείμενα.» Τα αντικείμενα αυτά μπορεί να είναι κύκλος, σημείο, ευθεία και προκύπτουν συνολικά 10 επιμέρους προβλήματα.
Στην παρούσα δημοσίευση διαπραγματευόμαστε το πρόβλημα: Nα γραφεί κύκλος που διέρχεται από δύο διακεκριμένα σημεία και εφάπτεται δεδομένου κύκλου. Η παρουσίαση και η λύση του προβλήματος γίνεται με Ευκλείδεια γεωμετρία και οι κατασκευές γίνονται με κανόνα και διαβήτη. Η αναλυτική λύση του προβλήματος χρησιμοποιεί φυσικά τη αναλυτική και συνθετική μέθοδο που δυστυχώς έχει αφαιρεθεί από τη διδακτέα ύλη της Γεωμετρίας στο Ελληνικό Λύκειο.
Μπορείτε να δείτε το αρχείο πατώντας εδώ.
Στα αρχεία της δημοσίευσης περιλαμβάνεται και το εργαλείο apollonius.ppc που δημιουργεί τη λύση του προβλήματος σε κάθε περίπτωση. Για να κατεβάσετε τα αρχεία geogebra κάνετε κλικ επάνω στην εικόνα.
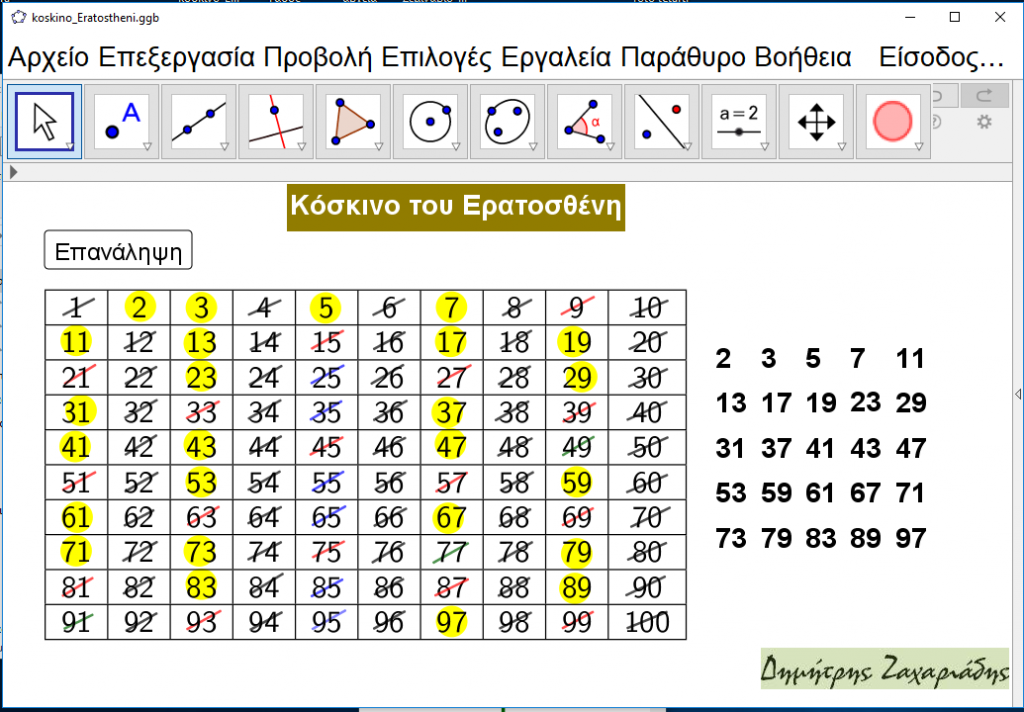
Δημοσιεύουμε αρχείο Geogebra που προσδιορίζει τους πρώτους αριθμούς από 1 έως 100 με την μέθοδο του Ερατοσθένη με σχετικό κείμενο που επεξηγεί την μέθοδο. Ίσως φανεί χρήσιμο σε όποιους θελήσουν να το διδάξουν. Για την λήψη των αρχείων κάνετε κλικ εδώ.
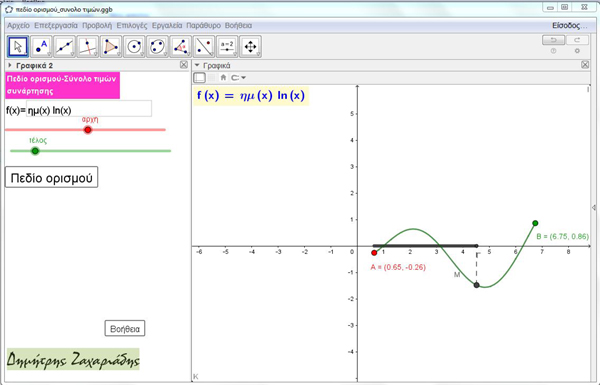
ΠΕΔΙΟ ΟΡΙΣΜΟΥ – ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΑΡΤΗΣΗΣ
Η φιλοσοφία της εφαρμογής είναι: Να μπορέσει ο μαθητής να αναγνωρίζει γραφικά το πεδίο ορισμού και το σύνολο τιμών συνάρτησης.
Βήματα της εφαρμογής. Δίνουμε τον τύπο συνάρτησης f, ορίζουμε γραφικά την αρχή και το τέλος του διαγράμματος δηλαδή τον περιορισμό της f σε ένα διάστημα [α,β] και το αρχείο μας σχεδιάζει, μετά από επιλογή μας, το πεδίο ορισμού και το σύνολο τιμών.
Όλα αυτά γίνονται με διαδοχικά βήματα ώστε να δίνεται η ευκαιρία στον μαθητή να μαντεύσει, να δώσει την απάντησή του πριν την εποπτική παρουσίαση που δίνει η εφαρμογή. Έτσι έχουμε ένα εργαλείο για την διδασκαλία και κατανόηση των αντίστοιχων εννοιών.
Η εφαρμογή δίνεται σε δύο εκδόσεις:
α) Η συνάρτηση f δεν είναι συνεχής και ορισμένη στο R και ούτε ο περιορισμός της είναι ορισμένη συνεχής στο διάστημα [α,β]. Τα αποτελέσματα δίνονται μόνο γραφικά
β) Η συνάρτηση f δεν είναι συνεχής και ορισμένη στο R, αλλά ο περιορισμός της στο [α,β] να είναι ορισμένη και συνεχής. Τα αποτελέσματα δίνονται και αλγεβρικά.
Προσοχή: Η εφαρμογή έχει περισσότερο διδακτική και λιγότερο υπολογιστική αξία.
Για να κατεβάσετε τα αρχεία κάνετε κλικ εδώ.
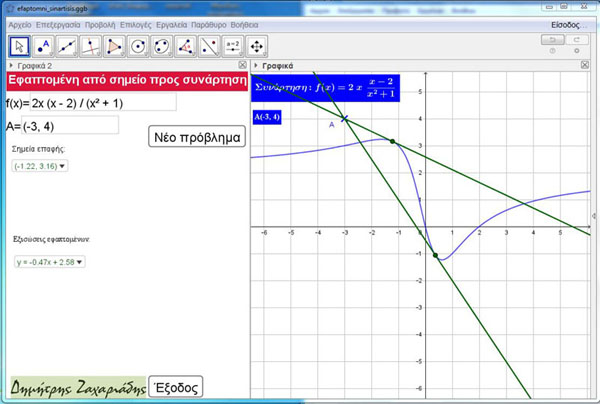
Το εργαλείο του Geogebra “εφαπτομένη προς κύκλο, κωνική ή συνάρτηση”, στην περίπτωση των συναρτήσεων, λειτουργεί σωστά μόνο για σημεία που βρίσκονται επί της γραφικής παράστασης. Στην περίπτωση όμως που θα θέλαμε να φέρουμε εφαπτόμενες προς την καμπύλη της συνάρτησης από σημεία που βρίσκονται εκτός αυτής, το λογισμικό παρουσιάζει προβλήματα αδυνατώντας, τις περισσότερες φορές, να δώσει τις αναμενόμενες απαντήσεις.
Ο συνάδελφος και φίλος Παύλος Τρύφωνας είχε την ιδέα να κατασκευαστεί ένα εργαλείο που να προσδιορίζει σε κάθε περίπτωση τις εφαπτόμενες από σημείο προς τη γραφική παράσταση μίας συνάρτησης. Το αρχείο που δημοσιεύω ανταποκρίνεται σε ικανοποιητικό βαθμό στο αίτημα αυτό.
Για να κατεβάσετε τα αρχεία πατήστε εδώ.
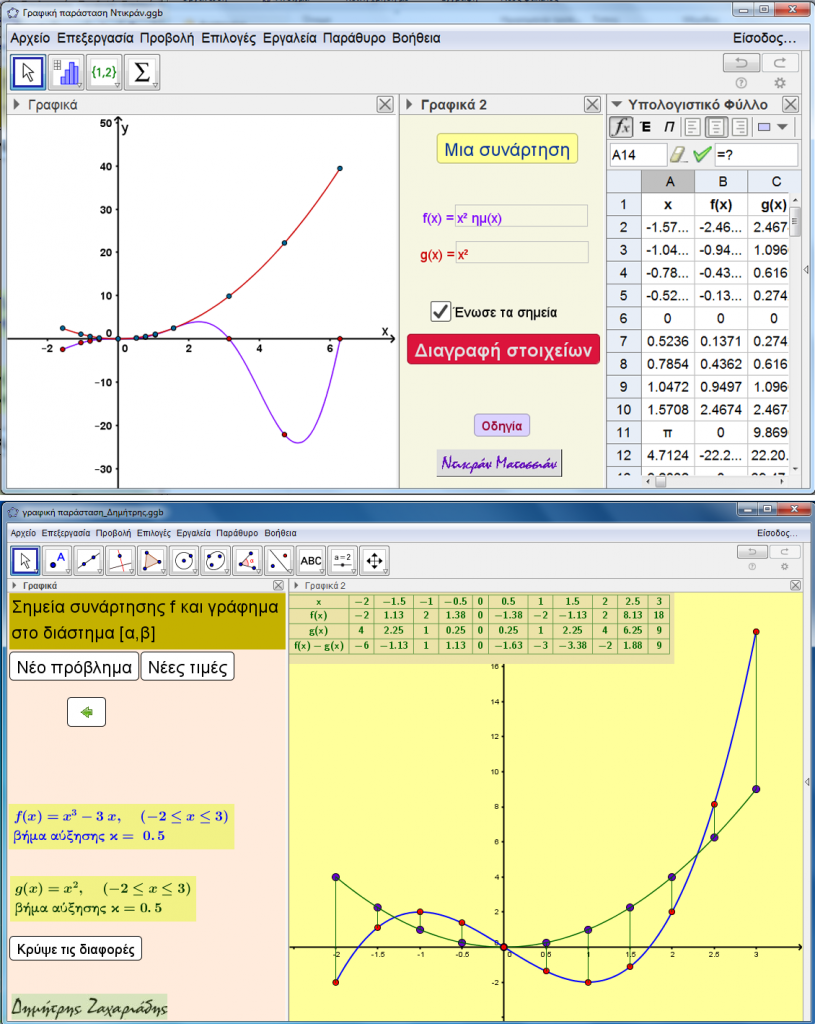
Πριν από λίγο καιρό αγαπητός συνάδελφος μας ζήτησε να κατασκευάσουμε ένα αρχείο Geogebra στο οποίο να δίνουμε τιμές στην ανεξάρτητη μεταβλητή και να υπολογίζει την αντίστοιχη τιμή της συνάρτησης και παράλληλα να εμφανίζει το αντίστοιχο σημείο της γραφικής παράστασης σε σύστημα συντεταγμένων.
Ανταποκρινόμενοι στο αίτημα του κατασκευάσαμε δύο αρχεία το καθένα με τη δική του φιλοσοφία, τα οποία σκεφτήκαμε και να δημοσιεύσουμε…
Για να κατεβάσετε τα αρχεία πατήστε επάνω στην εικόνα.
Δημήτρης-Ντικράν
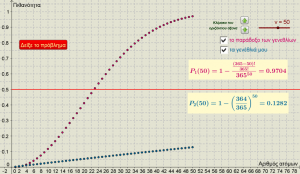
Το παράδοξο των γενεθλίων στη θεωρία πιθανοτήτων αναφέρεται σε ένα πρόβλημα το οποίο, κατά την κοινή λογική, έχει μια απίθανη απάντηση. Μία από τις μορφές του προβλήματος είναι: “σε μία ομάδα 23 ατόμων τι πιθανότητα υπάρχει δύο από αυτά τα άτομα να έχουν την ίδια ημέρα γενέθλια”; Η “πιθανά προφανής” απάντηση είναι 23/365=0,063 δηλαδή έξι τοις εκατό. Η μαθηματική λύση όμως μας δίνει 50%! Ακόμα πιο εντυπωσιακά, το ποσοστό γίνεται 99% με μόνο 57 άτομα! Στην εφαρμογή που αναρτούμε υπολογίζεται η πιθανότητα αυτή για διαφορετικά πλήθη ατόμων. Επίσης, υπολογίζεται και η πιθανότητα ύπαρξης της ίδιας μέρας γενεθλίων με συγκεκριμένο άτομο της ομάδας, ανεξάρτητα ή και σε αντιδιαστολή με την προηγούμενη πιθανότητα.
Θα μπορούσε να διδαχθεί στο μάθημα των πιθανοτήτων τόσο στην Α’ Λυκείου, όσο και στα Μαθηματικά Γενικής Παιδείας στη Γ’ Λυκείου.
Για να μεταφορτώσετε την εφαρμογή πιέστε επάνω στην εικόνα.