Άρθρα: Μαθηματικά Γενικής Παιδείας
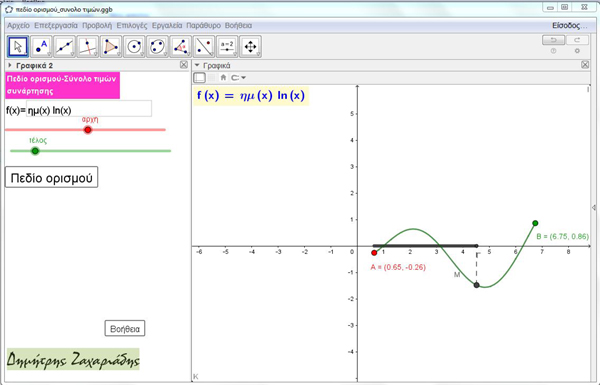
ΠΕΔΙΟ ΟΡΙΣΜΟΥ – ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΑΡΤΗΣΗΣ
Η φιλοσοφία της εφαρμογής είναι: Να μπορέσει ο μαθητής να αναγνωρίζει γραφικά το πεδίο ορισμού και το σύνολο τιμών συνάρτησης.
Βήματα της εφαρμογής. Δίνουμε τον τύπο συνάρτησης f, ορίζουμε γραφικά την αρχή και το τέλος του διαγράμματος δηλαδή τον περιορισμό της f σε ένα διάστημα [α,β] και το αρχείο μας σχεδιάζει, μετά από επιλογή μας, το πεδίο ορισμού και το σύνολο τιμών.
Όλα αυτά γίνονται με διαδοχικά βήματα ώστε να δίνεται η ευκαιρία στον μαθητή να μαντεύσει, να δώσει την απάντησή του πριν την εποπτική παρουσίαση που δίνει η εφαρμογή. Έτσι έχουμε ένα εργαλείο για την διδασκαλία και κατανόηση των αντίστοιχων εννοιών.
Η εφαρμογή δίνεται σε δύο εκδόσεις:
α) Η συνάρτηση f δεν είναι συνεχής και ορισμένη στο R και ούτε ο περιορισμός της είναι ορισμένη συνεχής στο διάστημα [α,β]. Τα αποτελέσματα δίνονται μόνο γραφικά
β) Η συνάρτηση f δεν είναι συνεχής και ορισμένη στο R, αλλά ο περιορισμός της στο [α,β] να είναι ορισμένη και συνεχής. Τα αποτελέσματα δίνονται και αλγεβρικά.
Προσοχή: Η εφαρμογή έχει περισσότερο διδακτική και λιγότερο υπολογιστική αξία.
Για να κατεβάσετε τα αρχεία κάνετε κλικ εδώ.
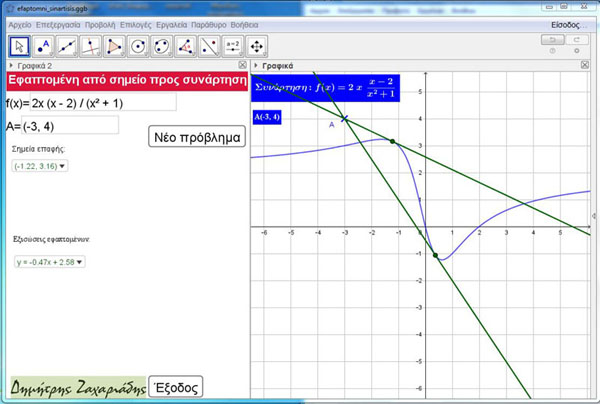
Το εργαλείο του Geogebra “εφαπτομένη προς κύκλο, κωνική ή συνάρτηση”, στην περίπτωση των συναρτήσεων, λειτουργεί σωστά μόνο για σημεία που βρίσκονται επί της γραφικής παράστασης. Στην περίπτωση όμως που θα θέλαμε να φέρουμε εφαπτόμενες προς την καμπύλη της συνάρτησης από σημεία που βρίσκονται εκτός αυτής, το λογισμικό παρουσιάζει προβλήματα αδυνατώντας, τις περισσότερες φορές, να δώσει τις αναμενόμενες απαντήσεις.
Ο συνάδελφος και φίλος Παύλος Τρύφωνας είχε την ιδέα να κατασκευαστεί ένα εργαλείο που να προσδιορίζει σε κάθε περίπτωση τις εφαπτόμενες από σημείο προς τη γραφική παράσταση μίας συνάρτησης. Το αρχείο που δημοσιεύω ανταποκρίνεται σε ικανοποιητικό βαθμό στο αίτημα αυτό.
Για να κατεβάσετε τα αρχεία πατήστε εδώ.
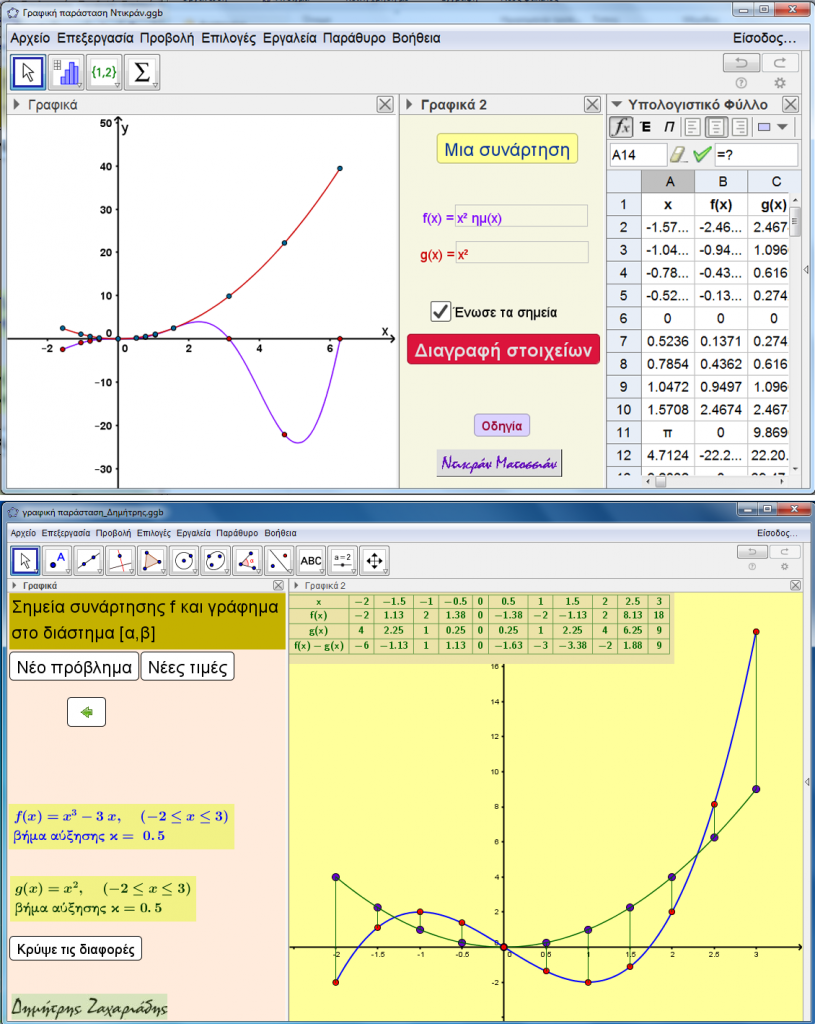
Πριν από λίγο καιρό αγαπητός συνάδελφος μας ζήτησε να κατασκευάσουμε ένα αρχείο Geogebra στο οποίο να δίνουμε τιμές στην ανεξάρτητη μεταβλητή και να υπολογίζει την αντίστοιχη τιμή της συνάρτησης και παράλληλα να εμφανίζει το αντίστοιχο σημείο της γραφικής παράστασης σε σύστημα συντεταγμένων.
Ανταποκρινόμενοι στο αίτημα του κατασκευάσαμε δύο αρχεία το καθένα με τη δική του φιλοσοφία, τα οποία σκεφτήκαμε και να δημοσιεύσουμε…
Για να κατεβάσετε τα αρχεία πατήστε επάνω στην εικόνα.
Δημήτρης-Ντικράν
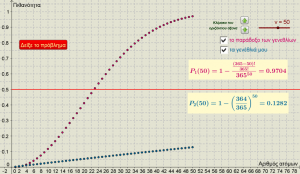
Το παράδοξο των γενεθλίων στη θεωρία πιθανοτήτων αναφέρεται σε ένα πρόβλημα το οποίο, κατά την κοινή λογική, έχει μια απίθανη απάντηση. Μία από τις μορφές του προβλήματος είναι: “σε μία ομάδα 23 ατόμων τι πιθανότητα υπάρχει δύο από αυτά τα άτομα να έχουν την ίδια ημέρα γενέθλια”; Η “πιθανά προφανής” απάντηση είναι 23/365=0,063 δηλαδή έξι τοις εκατό. Η μαθηματική λύση όμως μας δίνει 50%! Ακόμα πιο εντυπωσιακά, το ποσοστό γίνεται 99% με μόνο 57 άτομα! Στην εφαρμογή που αναρτούμε υπολογίζεται η πιθανότητα αυτή για διαφορετικά πλήθη ατόμων. Επίσης, υπολογίζεται και η πιθανότητα ύπαρξης της ίδιας μέρας γενεθλίων με συγκεκριμένο άτομο της ομάδας, ανεξάρτητα ή και σε αντιδιαστολή με την προηγούμενη πιθανότητα.
Θα μπορούσε να διδαχθεί στο μάθημα των πιθανοτήτων τόσο στην Α’ Λυκείου, όσο και στα Μαθηματικά Γενικής Παιδείας στη Γ’ Λυκείου.
Για να μεταφορτώσετε την εφαρμογή πιέστε επάνω στην εικόνα.
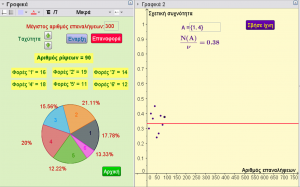
Στη θεωρία Πιθανοτήτων ο νόμος των μεγάλων αριθμών περιγράφει το αποτέλεσμα της επανάληψης ενός πειράματος τύχης. Σύμφωνα με το νόμο αυτό, ο μέσος όρος των αποτελεσμάτων που έχουν πραγματοποιηθεί σε διαδοχικές επαναλήψεις του πειράματος προσεγγίζει την αναμενόμενη τιμή (θεωρητική μέση τιμή) του πειράματος, όσο ο αριθμός των επαναλήψεων αυξάνει, Από αυτό προκύπτει ότι όταν το πλήθος των δοκιμών ενός πειράματος τύχης αυξάνει απεριόριστα, η σχετική συχνότητα ενός εκάστου ενδεχομένου προσεγγίζει τη θεωρητική του πιθανότητα. Η εφαρμογή που αναρτάται αναπαριστά το συγκεκριμένο νόμο στις περιπτώσεις του νομίσματος και του ζαριού. Ο χρήστης μπορεί να επιλέξει το συνολικό αριθμό ρίψεων καθώς επίσης και το ενδεχόμενο που σας ενδιαφέρει (στην περίπτωση του νομίσματος Κεφάλι ή Γράμματα, ενώ στην περίπτωση του ζαριού οποιοδήποτε απλό ή σύνθετο ενδεχόμενο).
Η εφαρμογή βασίζεται στην ακόλουθη ιδέα: δημιουργεί μια λίστα, μήκους ν0 (που καθορίζεται από το χρήστη και παριστάνει το συνολικό αριθμό ρίψεων), τυχαίων αριθμών (στη περίπτωση του νομίσματος είναι {Κεφάλι ή Γράμματα} ενώ στην περίπτωση του ζαριού {1, 2, 3, 4, 5 ή 6}. Δημιουργείται, στη συνέχεια , ένας δρομέας ν που ανατρέχει τη λίστα που έχει δημιουργηθεί, ανά δέκα στοιχεία, και μετρά τον αριθμό των απλών ή σύνθετων (στην περίπτωση του ζαριού) ενδεχομένων του πειράματος που έχουν προκύψει μέχρι την τρέχουσα τιμή του ν.
Θα μπορούσε να διδαχθεί στο μάθημα των πιθανοτήτων τόσο στην Α’, όσο και στα Μαθηματικά Γενικής Παιδείας στη Γ’ Λυκείου.
Για να μεταφορτώσετε την εφαρμογή πατήστε πάνω στην εικόνα.
 Δημοσιεύουμε το αρχείο αυτό που αφορά τον υπολογισμό του ορίου συνάρτησης και των ασύμπτωτων της.
Δημοσιεύουμε το αρχείο αυτό που αφορά τον υπολογισμό του ορίου συνάρτησης και των ασύμπτωτων της.
Δίνοντας τον τύπο της συνάρτησης και το x0 έχουμε την γραφική παράσταση της f σε περιοχή του x0.
Η έννοια του ορίου αισθητοποιείται με εμφάνιση της γραφικής παράστασης της συνάρτησης με κίνηση προς το x0 από τα δεξιά, από τα αριστερά, ή συγχρόνως.
Το αρχείο μπορεί να χρησιμοποιηθεί στη διδασκαλία των αντιστοίχων ενοτήτων στην Γ΄ Λυκείου.
Για να κατεβάσετε το αρχείο πατήστε επάνω στην εικόνα.
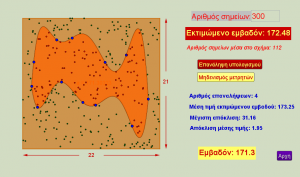
Ας υποθέσουμε ότι θα επιθυμούσαμε να υπολογίσουμε το εμβαδόν μιας επίπεδης μορφής για την οποία δεν υπάρχει κανένας τύπος που να την υπολογίζει επακριβώς. Υπάρχουν αρκετές μέθοδοι για να μπορέσουμε να το εκτιμήσουμε, όμως μια από τις πιο διασκεδαστικές είναι η ονομαζόμενη μέθοδος Monte Carlo που βασίζεται στις εαναλαμβανόμενες τυχαίες δειγματοληψίες. Η ιδέα είναι απλή: αρκεί να περιγράψουμε τη συγκεκριμένη μορφή με ένα ορθογώνιο του οποίου το εμβαδόν υπολογίζεται εύκολα, και στη συνέχεια να δημιουργήσουμε έναν αριθμό τυχαίων σημείων μέσα στο ορθογώνιο (π.χ. κρεμώντας το όλο σχήμα στον τοίχο και ρίχνοντας πάνω του βελάκια χωρίς να σημαδεύουμε)… Τότε αν δημιουργήσαμε 100 τέτοια σημεία μέσα στο ορθογώνιο, και από αυτά τα 60 κατέληξαν να είναι μέσα στην «περίεργη» μορφή, τότε το εκτιμώμενο εμβαδόν θα αντιστοιχεί στο 60% του εμβαδού του ορθογωνίου. Η συγκεκριμένη εφαρμογή αναπαριστά αυτή τη μέθοδο εκτίμησης εμβαδού, αλλά επιπλέον δείχνει και μια εφαρμογή της συγκεκριμένης μεθόδου στον υπολογισμό του π.
Θα μπορούσε να διδαχθεί στο μάθημα των πιθανοτήτων τόσο στην Α’, όσο και στα Μαθηματικά Γενικής Παιδείας στη Γ’ Λυκείου.
Για να μεταφορτώσετε το αρχείο κάνετε κλικ επάνω στην εικόνα.