Άρθρα: Β΄ Λυκείου
Δημοσιεύουμε αρχείο που δείχνει με βήματα την κατασκευή της χρυσής τομής του χρυσού ορθογώνιου και της χρυσής σπείρας.
Το ενδιαφέρον και η πρωτοτυπία του είναι η χρήση της εντολής ΛίσταΕπανάληψης για τον σχηματισμό λίστας σημείων που χρειάζονται για τον σχηματισμό της Χρυσής σπείρας. Με την χρήση αυτής της εντολής δεν χρειάζεται να δημιουργήσουμε ένα – ένα τα κομμάτια της κατασκευής αλλά μπορούμε να φθάσουμε απευθείας στο τελικό αποτέλεσμα.
Μαζί με το αρχείο Geogebra δημοσιεύουμε και ένα κείμενο με οδηγίες και παραδείγματα για την εντολή αυτή.
Για να κατεβάσετε το αρχείο Geogebra και το κείμενο με τις οδηγίες πατήστε εδώ.
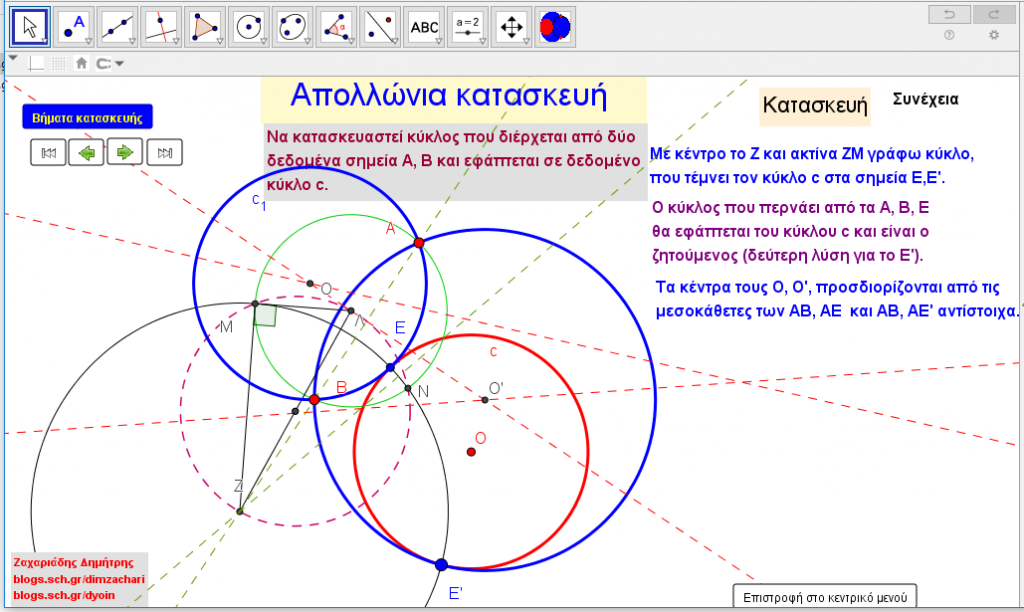
Η δημοσίευση αυτή είναι η τρίτη με τον ίδιο γενικό τίτλο, «Απολλώνιο Πρόβλημα».
Το Απολλώνιο Πρόβλημα «να γραφεί κύκλος που να εφάπτεται σε τρεις δεδομένους κύκλους», λυμένο από τον μεγάλο μαθηματικό της αρχαιότητας Απολλώνιο τον Περγαίο, είναι το κορυφαίο πρόβλημα, από μια σειρά επί μέρους προβλημάτων των οποίων η επίλυση οδηγεί σταδιακά στην λύση του.
Τα προβλήματα αυτά έχουν τη γενική διατύπωση: «Να γραφεί κύκλος που εφάπτεται σε τρία αντικείμενα.» Τα αντικείμενα αυτά μπορεί να είναι κύκλος, σημείο, ευθεία και προκύπτουν συνολικά 10 επιμέρους προβλήματα.
Στην παρούσα δημοσίευση διαπραγματευόμαστε το πρόβλημα: Nα γραφεί κύκλος που διέρχεται από δύο διακεκριμένα σημεία και εφάπτεται δεδομένου κύκλου. Η παρουσίαση και η λύση του προβλήματος γίνεται με Ευκλείδεια γεωμετρία και οι κατασκευές γίνονται με κανόνα και διαβήτη. Η αναλυτική λύση του προβλήματος χρησιμοποιεί φυσικά τη αναλυτική και συνθετική μέθοδο που δυστυχώς έχει αφαιρεθεί από τη διδακτέα ύλη της Γεωμετρίας στο Ελληνικό Λύκειο.
Μπορείτε να δείτε το αρχείο πατώντας εδώ.
Στα αρχεία της δημοσίευσης περιλαμβάνεται και το εργαλείο apollonius.ppc που δημιουργεί τη λύση του προβλήματος σε κάθε περίπτωση. Για να κατεβάσετε τα αρχεία geogebra κάνετε κλικ επάνω στην εικόνα.
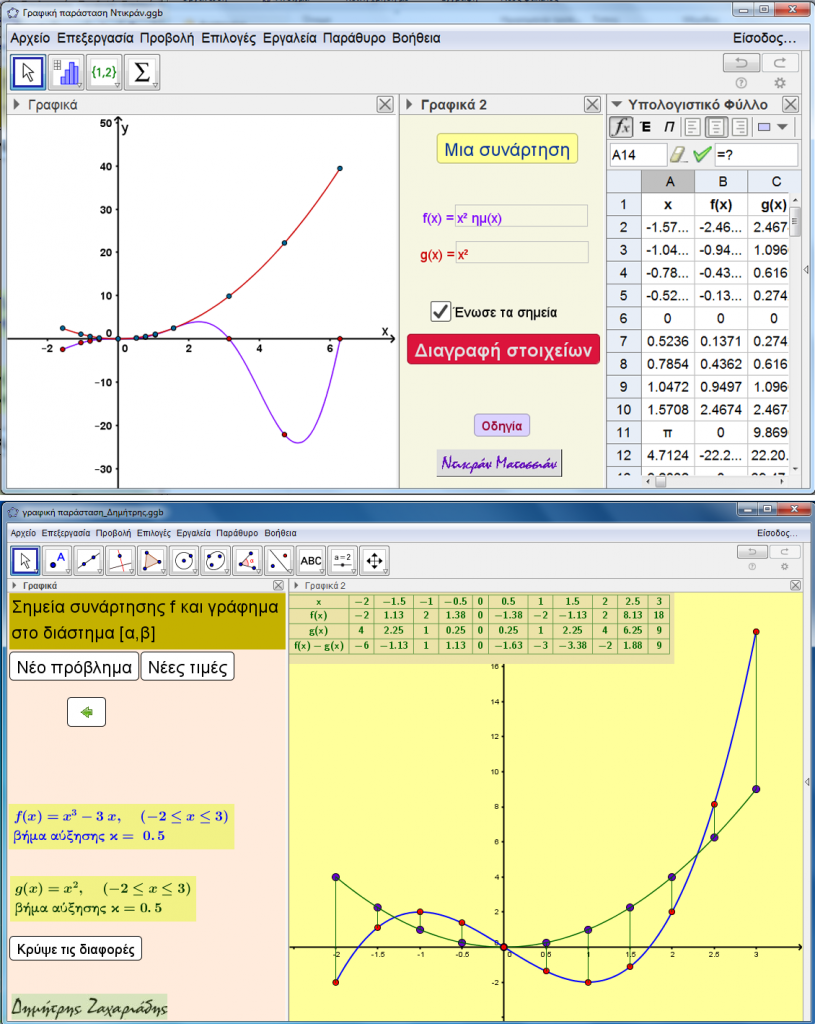
Πριν από λίγο καιρό αγαπητός συνάδελφος μας ζήτησε να κατασκευάσουμε ένα αρχείο Geogebra στο οποίο να δίνουμε τιμές στην ανεξάρτητη μεταβλητή και να υπολογίζει την αντίστοιχη τιμή της συνάρτησης και παράλληλα να εμφανίζει το αντίστοιχο σημείο της γραφικής παράστασης σε σύστημα συντεταγμένων.
Ανταποκρινόμενοι στο αίτημα του κατασκευάσαμε δύο αρχεία το καθένα με τη δική του φιλοσοφία, τα οποία σκεφτήκαμε και να δημοσιεύσουμε…
Για να κατεβάσετε τα αρχεία πατήστε επάνω στην εικόνα.
Δημήτρης-Ντικράν
 Limnos 14_12_2015 Limnos 17_12_2015
Limnos 14_12_2015 Limnos 17_12_2015
Κατόπιν απόφασης του Περιφερειακού Διευθυντή Α/θμιας & Β/θμιας Εκπαίδευσης Βορείου Αιγαίου Αριστείδη Καλάργαλη και θετικής εισήγησης του Προϊστάμενου Επιστημονικής & Παιδαγωγικής Καθοδήγησης Β/θμιας Εκπ/σης Β. Αιγαίου κ. Πρόδρομου Ελευθερίου, διοργανώθηκε από το Σχολικό Σύμβουλο ΠΕ03 της Δ/νσης Β/θμιας Εκπ/σης Σάμου με αρμοδιότητα και στις περιοχές Ν. Χίου και Λέσβου κ. Ιωάννη Ράλλη, την 15η Δεκεμβρίου 2015 στη Λήμνο, επιμορφωτική συνάντηση με θέμα τη «Χρήση του λογισμικού Geogebra στη διδασκαλία των Μαθηματικών», στην οποία ήταν εισηγητής ο συνάδελφος και φίλος Δημήτρης Ζαχαριάδης.
Στο περιθώριο της συνάντησης αυτής, παρουσίασε δύο δειγματικές διδασκαλίες. Η πρώτη έγινε στις 14 Δεκεμβρίου, στη Β’ Λυκείου του Λυκείου Μούδρου, με θέμα τη μελέτη των τριγωνομετρικών συναρτήσεων και ιδιαίτερα μελέτη και γραφική παράσταση της συνάρτησης εφαπτομένη. Η δεύτερη έγινε στις 17 Δεκεμβρίου, στη Β’ Λυκείου του Λυκείου Μύρινας, με θέμα τη μελέτη των τριγωνομετρικών συναρτήσεων ημίτονο και συνημίτονο και μελέτη της συνάρτησης f(x)=ρημωx με ρ≠0 και ω>0
Μπορείτε να μεταφορτώσετε το υλικό της πρώτης δειγματικής διδασκαλίας πατώντας εδώ και της δεύτερης πατώντας εδώ.
Το διήμερο 20 και 21 Νοεμβρίου 2015 ο συνάδελφος και φίλος Δημήτρης Ζαχαριάδης μετέβη στην Χίο, κατόπιν πρόσκλησης του Σχολικού Συμβούλου ΠΕ03 της Δ/νσης Β/θμιας Εκπ/σης Σάμου με αρμοδιότητα και στις περιοχές Ν. Χίου και Λέσβου κ. Ιωάννη Ράλλη και του τοπικού παραρτήματος της ΕΜΕ, ώστε να συμμετάσχει σε επιμορφωτική συνάντηση με θέμα τη «Χρήση του λογισμικού Geogebra στη διδασκαλία των Μαθηματικών». Στα πλαίσια της συνάντησης αυτής, την 20η Νοεμβρίου παρουσίασε μια δειγματική διδασκαλία στη Β’ Λυκείου του 1ου Λυκείου Χίου, με θέμα τη μελέτη και γραφική παράσταση της συνάρτησης ημίτονο. Η διδασκαλία έγινε σε Εργαστήριο Πληροφορικής με τους μαθητές να συμπληρώνουν το φύλλο εργασίας με τη βοήθεια εφαρμογών Geogebra που δημιουργήθηκαν γι’ αυτόν το σκοπό. Μπορείτε να μεταφορτώσετε το υλικό της δειγματικής διδασκαλίας πατώντας στη φωτογραφία.
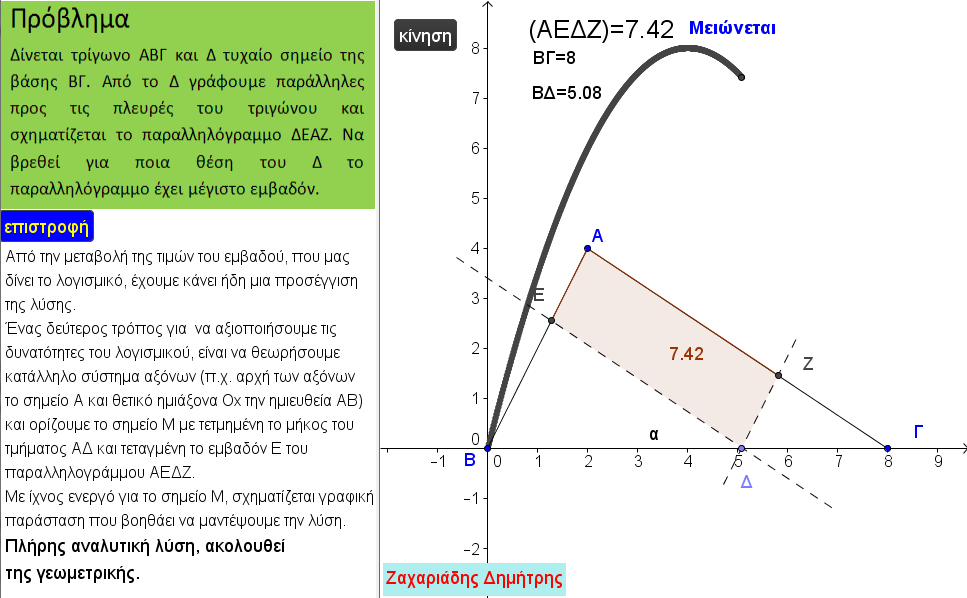
Η εφαρμογή που δημοσιεύουμε αφορά ένα πρόβλημα γεωμετρίας, που αναφέρεται στον προσδιορισμό του μεγίστου εμβαδού ενός παραλληλογράμμου εγγεγραμμένου σε τρίγωνο.
Η εφαρμογή αυτή μπορεί να διδαχθεί στην Β΄ Λυκείου και γενικά στο Λύκειο, κατά την κρίση του διδάσκοντος.
Με την βοήθεια του λογισμικού δίνεται η ευκαιρία στον μαθητή να μαντέψει ενορατικά την λύση και στην συνέχεια παρουσιάζονται με βήματα λύσεις, γεωμετρική, αλγεβρική και αναλυτική και μπορούν να στηθούν πολλά σενάρια διδασκαλίας.
Παρουσιάζει μεγάλο διδακτικό ενδιαφέρον γιατί εμπλέκονται πολλές ενότητες από την ύλη των μαθηματικών όπως οι παρακάτω:
- Όμοια τρίγωνα
- Μετρικές σχέσεις εμβαδών τριγώνου
- Τριγωνομετρία
- Μετρικές σχέσεις ορθογωνίου τριγώνου.
- Μελέτη και γραφική παράσταση τριωνύμου
- Αλγεβρικές ταυτότητες.
Μπορείτε να δείτε το αρχείο on line κάνοντας κλικ επάνω στην εικόνα.
Για να κατεβάσετε το αρχείο κάντε κλικ εδώ
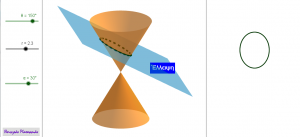
Μέχρι τώρα, στην εισαγωγή της έννοιας της κωνικής τομής, στην Β’ Λυκείου, αν θέλαμε να αναπαραστήσουμε με έναν πειστικά εποπτικό τρόπο τον ορισμό της σύμφωνα με τον Απολλώνιο τον Περγαίο, θα έπρεπε να αναζητήσουμε αντίστοιχες εφαρμογές στο διαδίκτυο. Η νέα έκδοση του Geogebra μας δίνει τη δυνατότητα σχεδιασμού γεωμετρικών αντικειμένων στο χώρο με απλό τρόπο. Η εφαρμογή που παρουσιάζουμε δίνει τη δυνατότητα στο μαθητή ή τον καθηγητή μετακινώντας το επίπεδο τομής ενός κώνου, να βλέπει την αντίστοιχη καμπύλη τομής που προκύπτει.
Για να μεταφορτώσετε το αρχείο πατήστε πάνω στην εικόνα.
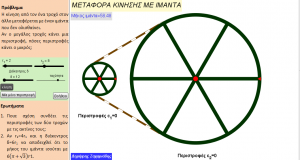 Με αφορμή μια άσκηση του σχολικού βιβλίου της Β΄ Γυμνασίου, στην ενότητα «Μέτρηση κύκλου-τόξου», δημιουργήθηκε το αρχείο αυτό που δίνει μα αναπαράσταση του προβλήματος.
Με αφορμή μια άσκηση του σχολικού βιβλίου της Β΄ Γυμνασίου, στην ενότητα «Μέτρηση κύκλου-τόξου», δημιουργήθηκε το αρχείο αυτό που δίνει μα αναπαράσταση του προβλήματος.
Μπορεί να διδαχθεί και στην Β΄ Λυκείου. Με το κουμπί «Βοήθεια» δίνεται η δυνατότητα επίδειξης του τρόπου κατασκευής της κοινής εφαπτομένης δύο κύκλων, και αφήνεται στο διδάσκοντα να επιλέξει αν θα το διδάξει.
Στην κατασκευή του αρχείου χρησιμοποιήθηκαν οι εντολές ΔείξεΣτρώση[ ] και ΑπόκρυψηΣτρώσης[ ] του λογισμικού.
Για να κατεβάσετε το αρχείο πατήστε επάνω στην εικόνα.
Η δημοσίευση αυτή είναι η δεύτερη από μια σειρά δημοσιεύσεων που σκοπεύουμε να κάνουμε επάνω στο “Απολλώνιο Πρόβλημα”.
Το Απολλώνιο Πρόβλημα «να γραφεί κύκλος που να εφάπτεται σε τρεις δεδομένους κύκλους», λυμένο από τον μεγάλο μαθηματικό της αρχαιότητας Απολλώνιο τον Περγαίο, είναι το κορυφαίο πρόβλημα από μια σειρά επί μέρους προβλημάτων, των οποίων η επίλυση οδηγεί σταδιακά στην λύση του.
Τα προβλήματα αυτά έχουν τη γενική διατύπωση: «Να γραφεί κύκλος που εφάπτεται σε τρία αντικείμενα.» Τα αντικείμενα αυτά μπορεί να είναι κύκλος, σημείο, ευθεία και προκύπτουν συνολικά 10 επιμέρους προβλήματα.
Στην παρούσα δημοσίευση διαπραγματευόμαστε το πρόβλημα, να γραφεί κύκλος που διέρχεται από γνωστό σημείο και εφάπτεται δύο δεδομένων ευθειών. Όλα αυτά επιλύονται με Ευκλείδεια γεωμετρία και οι κατασκευές γίνονται με κανόνα και διαβήτη.
Ενδεικτικά γράφουμε, β΄Λυκείου Γεωμετρία παρόλο που το πρόβλημα και η σχετική ύλη δεν είναι στην διδακτέα ύλη της τάξης αυτής αλλά και γενικά στην ύλη του Λυκείου.
Στα αρχεία της δημοσίευσης περιλαμβάνεται και το εργαλείο apollonius.pll που δημιουργεί τη λύση του προβλήματος σε κάθε περίπτωση. Για να κατεβάσετε τα αρχεία κάνετε κλικ επάνω στην εικόνα.
Η δημοσίευση αυτή είναι η πρώτη από μια σειρά δημοσιεύσεων που σκοπεύουμε να κάνουμε επάνω στο “Απολλώνιο Πρόβλημα”.
Το Απολλώνιο Πρόβλημα «να γραφεί κύκλος που να εφάπτεται σε τρεις δεδομένους κύκλους», λυμένο από τον μεγάλο μαθηματικό της αρχαιότητας Απολλώνιο τον Περγαίο, είναι το κορυφαίο πρόβλημα από μια σειρά επί μέρους προβλημάτων, των οποίων η επίλυση οδηγεί σταδιακά στην λύση του.
Τα προβλήματα αυτά έχουν τη γενική διατύπωση: «Να γραφεί κύκλος που εφάπτεται σε τρία αντικείμενα.» Τα αντικείμενα αυτά μπορεί να είναι κύκλος, σημείο, ευθεία και προκύπτουν συνολικά 10 επιμέρους προβλήματα.
Στην παρούσα δημοσίευση διαπραγματευόμαστε το πρόβλημα, να γραφεί κύκλος που διέρχεται από δύο διακεκριμένα σημεία και εφάπτεται δεδομένης ευθείας. Όλα αυτά επιλύονται με Ευκλείδεια γεωμετρία και οι κατασκευές γίνονται με κανόνα και διαβήτη. Η αναλυτική λύση του προβλήματος χρησιμοποιεί φυσικά τη αναλυτική και συνθετική μέθοδο που δυστυχώς έχει αφαιρεθεί από τη διδακτέα ύλη της Γεωμετρίας στο Ελληνικό Λύκειο.
Στα αρχεία της δημοσιευσης περιλαμβάνεται και το εργαλείο apollonius.ppl που δημιουργεί τη λύση του προβλήματος σε κάθε περίπτωση. Για να κατεβάσετε τα αρχεία κάνετε κλικ επάνω στην εικόνα.