popiardv's blog

Οι μαθητές χωρίζονται σε ομάδες των 4 ή 6 .

Ανά δύο εργάζονται για να ανακαλύψουν το Πυθαγόρειο θεώρημα.

Ανταλλάσσουν τα ευρήματα τους στην ομάδα, φτιάχνουν κολάζ και τα παρουσιάζουν στην τάξη

ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ

ΓΙΑ ΜΑΘΗΤΕΣ Β΄ ΓΥΜΝΑΣΙΟΥ

ΟΜΑΔΑ 1

Μαθητές: ………………………. και ………………………

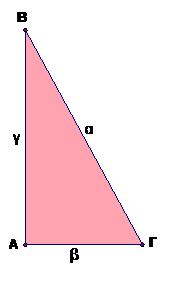
1)Σε χαρτί Α4, κατασκευάζουμε ορθογώνιο τρίγωνο ΑΒΓ με γωνία Α =90^ο

2) Μετράμε τα μήκη των πλευρών του και τα σημειώνουμε

ΑΒ=…………, ΑΓ=………….. , ΒΓ=……………

3) Κατασκευάζουμε 3 τετράγωνα ΑΒΖΗ, ΑΓΚΛ και ΒΓΜΝ έξω από το τρίγωνο.

4) Υπολογίζουμε τα εμβαδά των τετραγώνων

(ΑΒΖΗ) =……………………….

(ΑΓΚΛ) =………………………

(ΒΓΜΝ) =……………………….

5) Υπολογίζουμε το άθροισμα

(ΑΒΖΗ)+(ΑΓΚΛ) = …………………………..

6)Συγκρίνουμε το παραπάνω άθροισμα με το εμβαδόν του τετραγώνου ΒΓΜΝ

(ΑΒΖΗ) + (ΑΓΚΛ)………….. (ΒΓΜΝ)

7)Από τη σχέση του προηγούμενου ερωτήματος βρίσκουμε μια σχέση που ισχύει για τις πλευρές α, β, γ του ορθογωνίου τριγώνου

8)Συζητάμε με τα άλλα μέλη της ομάδας μας τα ευρήματά μας και τον τρόπο που καταλήξαμε σε αυτά.

ΟΜΑΔΑ 2

Μαθητές: …………………………… και …………………………

1) Σε χαρτί Α4, κατασκευάζουμε ορθογώνιο τρίγωνο ΑΒΓ(Α =90^ο)

με πλευρές ΑΒ=4 cm, ΑΓ=3cm

2)Σημειώνουμε το μήκος της πλευράς ΒΓ= ……… cm

3) Κατασκευάζουμε 3 τετράγωνα ΑΒΖΗ, ΑΓΚΛ και ΒΓΜΝ έξω από το τρίγωνο

4) Κόβουμε χαρτί τετραγωνισμένο και το κολλάμε κατάλληλα ώστε να εφαρμόσει πάνω στα τετράγωνα

5) Με μονάδα μέτρησης ……………. βρίσκουμε τα εμβαδά των τετραγώνων

(ΑΒΖΗ) = …… ……….

(ΑΓΚΛ) = …… ……….

(ΒΓΜΝ) = …… ……….

6) Υπολογίζουμε το άθροισμα

(ΑΒΖΗ) + (ΑΓΚΛ) =……………………..

7) Συγκρίνουμε το παραπάνω άθροισμα με το εμβαδόν του τετραγώνου ΒΓΜΝ :

(ΑΒΖΗ) + (ΑΓΚΛ)………….. (ΒΓΜΝ)

8)Από τη σχέση του προηγούμενου ερωτήματος βρίσκουμε μια σχέση που ισχύει για τις πλευρές α, β, γ του ορθογωνίου τριγώνου

9) Συζητάμε με τα άλλα μέλη της ομάδας μας τα ευρήματά μας και τον τρόπο που καταλήξαμε σε αυτά.

ΟΜΑΔΑ 2

Μαθητές: ………………………… και ………………………

1) Σε χαρτί Α4, κατασκευάζουμε ορθογώνιο τρίγωνο ΑΒΓ(Α =90^ο)

με πλευρές ΑΒ=8 cm, ΑΓ=6cm

2)Σημειώνουμε το μήκος της πλευράς ΒΓ= ……… cm

3) Κατασκευάζουμε 3 τετράγωνα ΑΒΖΗ, ΑΓΚΛ και ΒΓΜΝ έξω από το τρίγωνο

4) Κόβουμε χαρτί τετραγωνισμένο και το κολλάμε κατάλληλα ώστε να εφαρμόσει πάνω στα τετράγωνα

5) Με μονάδα μέτρησης ……………. βρίσκουμε τα εμβαδά των τετραγώνων

(ΑΒΖΗ) = …… ……….

(ΑΓΚΛ) = …… ……….

(ΒΓΜΝ) = …… ……….

6) Υπολογίζουμε το άθροισμα

(ΑΒΖΗ) + (ΑΓΚΛ) = ……………………..

7) Συγκρίνουμε το παραπάνω άθροισμα με το εμβαδόν του τετραγώνου ΒΓΜΝ :

(ΑΒΖΗ)+(ΑΓΚΛ)………….. (ΒΓΜΝ)

8)Από τη σχέση του προηγούμενου ερωτήματος βρίσκουμε μια σχέση που ισχύει για τις πλευρές α, β, γ του ορθογωνίου τριγώνου

9) Συζητάμε με τα άλλα μέλη της ομάδας μας τα ευρήματά μας και τον τρόπο που καταλήξαμε σε αυτά.

ΟΜΑΔΑ 2

Μαθητές: ……………………… και ………………………

1) Σε χαρτί Α4, κατασκευάζουμε ορθογώνιο τρίγωνο ΑΒΓ(Α =90^ο)

με πλευρές ΑΒ=12 cm, ΑΓ=5 cm

2)Σημειώνουμε το μήκος της πλευράς ΒΓ= ……… cm

3) Κατασκευάζουμε 3 τετράγωνα ΑΒΖΗ, ΑΓΚΛ και ΒΓΜΝ έξω από το τρίγωνο

4) Κόβουμε χαρτί τετραγωνισμένο και το κολλάμε κατάλληλα ώστε να εφαρμόσει πάνω στα τετράγωνα

5) Με μονάδα μέτρησης ……………. βρίσκουμε τα εμβαδά των τετραγώνων

(ΑΒΖΗ) = …… ……….

(ΑΓΚΛ) = …… ……….

(ΒΓΜΝ) = …… ……….

6) Υπολογίζουμε το άθροισμα

(ΑΒΖΗ) + (ΑΓΚΛ) = ……………………….

7) Συγκρίνουμε το παραπάνω άθροισμα με το εμβαδόν του τετραγώνου ΒΓΜΝ :

(ΑΒΖΗ)+(ΑΓΚΛ)………….. (ΒΓΜΝ)

8)Από τη σχέση του προηγούμενου ερωτήματος βρίσκουμε μια σχέση που ισχύει για τις πλευρές α, β, γ του ορθογωνίου τριγώνου

9) Συζητάμε με τα άλλα μέλη της ομάδας μας τα ευρήματά μας και τον τρόπο που καταλήξαμε σε αυτά.

ΟΜΑΔΑ 3

Μαθητές: ……………………… και ………………………

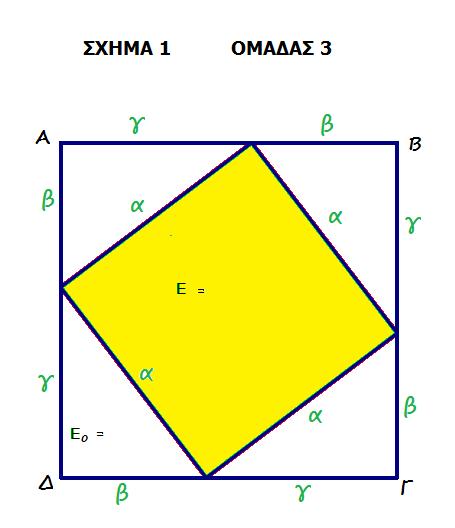
1) Συγκρίνουμε τα εμβαδά των παρακάτω τετραγώνων ΑΒΓΔ και ΚΛΜΝ και δικαιολογούμε την απάντησή μας

(ΑΒΓΔ) …. (ΚΛΜΝ) γιατί…………………………………………………………………

2) Υπολογίζουμε το εμβαδόν του τετραγώνου πλευράς α και των ίσων τριγώνων με πλευρές β, γ

Ε =

Εο =

3) Γράφουμε το εμβαδόν του τετραγώνου ΑΒΓΔ ως άθροισμα των εμβαδών των σχημάτων που το αποτελούν

(ΑΒΓΔ) =

ΟΜΑΔΑ 3

Μαθητές: …………………………… και ………………………

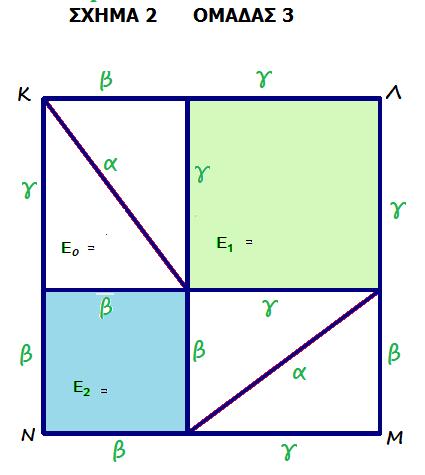
4) Υπολογίζουμε το εμβαδόν των τετραγώνων με πλευρά β και γ και των ίσων τριγώνων με πλευρές β, γ :

Ε1=

Ε2=

Εο =

5) Γράφουμε το εμβαδόν του τετραγώνου ΚΛΜΝ ως άθροισμα των εμβαδών των σχημάτων που το αποτελούν

(ΚΛΜΝ) =

6) Συζητάμε με τα μέλη της ομάδας μας τα ευρήματά μας και αξιοποιώντας την σύγκριση των εμβαδών των τετραγώνων ΑΒΓΔ και ΚΛΜΝ (ερώτημα 1) και τα ευρήματα των ερωτημάτων 3 και 5 συμπεραίνουμε μια σχέση που ισχύει για τα εμβαδά των τετραγώνων Ε1, Ε2 και Ε

7) Από τη σχέση του προηγούμενου ερωτήματος βρίσκουμε μια σχέση που ισχύει για τις πλευρές α, β, γ του ορθογωνίου τριγώνου

8) Συζητάμε με τα άλλα μέλη της ομάδας μας τα ευρήματά μας και τον τρόπο που καταλήξαμε σε αυτά.

9) Σχεδιάζουμε σε χαρτονάκι τα ευρήματα μας και γράφουμε τα συμπεράσματα μας

ΟΜΑΔΑ 4

Μαθητές: ………………………… και ………………………

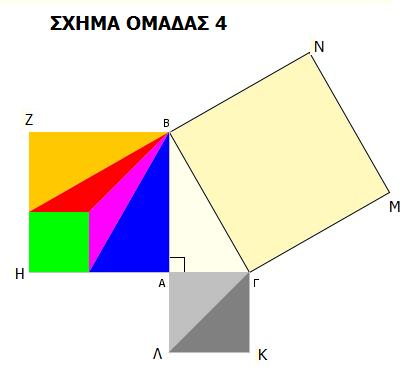
1)Μεταφέρουμε τα τετράγωνα ΑΒΖΗ και ΑΓΚΛ μέσα στο τετράγωνο ΒΓΝΜ

2) Το άθροισμα (ΑΒΖΗ) + (ΑΓΚΛ) = ……………………….

3) Συγκρίνουμε το παραπάνω άθροισμα με το εμβαδόν του τετραγώνου ΒΓΜΝ : (ΑΒΖΗ)+(ΑΓΚΛ)………….. (ΒΓΜΝ)

4)Από τη σχέση του προηγούμενου ερωτήματος βρίσκουμε μια σχέση που ισχύει για τις πλευρές α, β, γ του ορθογωνίου τριγώνου

5) Συζητάμε με τα άλλα μέλη της ομάδας μας τα ευρήματά μας και τον τρόπο που καταλήξαμε σε αυτά.

ΟΜΑΔΑ 5

Μαθητές: ……………………… και ………………………

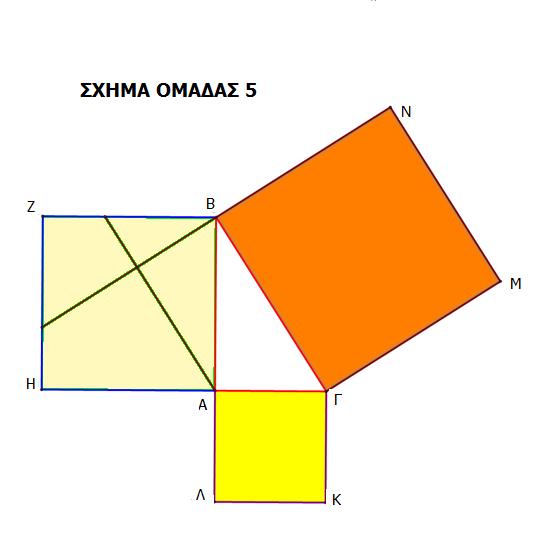
1)Κόβουμε τα τετράγωνα ΑΒΖΗ και ΑΓΚΛ και να τα τοποθετούμε μέσα στο τετράγωνο ΒΓΜΝ.

2) Το άθροισμα (ΑΒΖΗ) + (ΑΓΚΛ) = ……………………….

3) Συγκρίνουμε το παραπάνω άθροισμα με το εμβαδόν του τετραγώνου ΒΓΜΝ : (ΑΒΖΗ)+(ΑΓΚΛ)………….. (ΒΓΜΝ)

4)Από τη σχέση του προηγούμενου ερωτήματος βρίσκουμε μια σχέση που ισχύει για τις πλευρές α, β, γ του ορθογωνίου τριγώνου

5) Συζητάμε με τα άλλα μέλη της ομάδας μας τα ευρήματά μας και τον τρόπο που καταλήξαμε σε αυτά.

ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ

Να συμπληρώσετε τον κανόνα:

Σε κάθε ορθογώνιο τρίγωνο το άθροισμα των τετραγώνων των δύο ……………………. πλευρών

είναι ίσο με το τετράγωνο της …………………….. δηλαδή ΑΒ² + ΑΓ² = ….

ΑΠΟΔΕΙΞΕΙΣ ΤΟΥ ΠΥΘΑΓΟΡΕΙΟΥ ΘΕΩΡΗΜΑΤΟΣ:

Απόδειξη Liu Hui

Απόδειξη H.Dudeney

Απόδειξη Πυθαγόρα

Απόδειξη Ευκλείδη

Ετικέτες:Πυθαγόρειο