Απλά ένα ακόμα ιστολόγιο Blogs.sch.gr
21 Ιαν 2014 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Γνωρίζουμε το εμβαδόν μιας πισίνας. Μπορούμε να βρούμε τις διαστάσεις της; Πόσες λύσεις έχουμε;
Αν γίνει γνωστό και το άθροισμα των διαστάσεων της μπορούμε να προσδιορίσουμε καλύτερα τις διαστάσεις της; Πόσες λύσεις έχουμε σε αυτή τη περίπτωση;
Ας κάνετε τα πειράματα σας με το αρχείο Geogebra που θα ανοίξει πατώντας πάνω στην εικόνα της πισίνας
Εναλλακτικά μπορείτε να κάνετε λήψη του αρχείου από ΕΔΩ
17 Ιαν 2014 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Ο Πύργος του Ανόι
ένα ακόμη ενδιαφέρον παιχνίδι. Ο παίκτης πρέπει να μεταφέρει τους δίσκους του πύργου έναν-έναν σε μία άλλη στήλη, έχοντας βοηθητική μία τρίτη στήλη. Ένας σημαντικός κανόνας του παιχνιδιού είναι ότι δεν μπορεί να τοποθετηθεί ούτε μία φορά ένας δίσκος πάνω σε έναν μικρότερο του.
Πατήστε στην εικόνα που ακολουθεί για να παίξετε. Ξεκινάτε το παιχνίδι με 3 δίσκους στον πρώτο πύργο που πρέπει να τους μεταφέρετε στον τελευταίο (τρίτο πύργο). Μετά ανεβάζετε τη δυσκολία αυξάνοντας τον αριθμό τους.
Μία ενδιαφέρουσα ιστορική παρένθεση σχετικά με τον Πύργο του Ανόι λέει ο παρακάτω θρύλος με τίτλο:
« Πύργος του Βράχμα »
«Όταν ο Βράχμα δημιούργησε τον κόσμο, έστησε σε ένα ναό στην πόλη Μπενάρες, 64 δακτυλίδια άνισου μεγέθους όλα περασμένα σένα μπαστούνι έτσι ώστε αν κρατήσουμε το μπαστούνι κατακόρυφα να σχηματίζουν τον γνωστό μας πύργο.
Oι ιερείς του ναού έπρεπε να δουλεύουν μέρα νύχτα, χωρίς σταμάτημα, για να μεταφέρουν τα δακτυλίδια σένα άλλο μπαστούνι, χρησιμοποιώντας ένα τρίτο σαν βοηθητικό, έτσι ώστε να μην τοποθετήσουν μεγαλύτερο δακτυλίδι πάνω από μικρότερο και μετακινώντας ένα μόνο δακτυλίδι σε κάθε κίνηση.
Ο θρύλος λέει πως πριν προλάβουν οι ιερείς να μεταφέρουν όλα τα δακτυλίδια στο άλλο μπαστούνι, ο ναός θα καταρρεύσει μέσα στην σκόνη και ο κόσμος θα χαθεί μέσα σε τρομακτικό κρότο βροντής».
Είχε άραγε ο Βράχμα δίκιο;
Δείτε την απάντηση:
http://3gym-serron.ser.sch.gr/OLDSITE/Anoi.htm
Περισσότερες προκλήσεις με τον Πύργο του Ανόι εδώ:
http://www.cut-the-knot.org/recurrence/hanoi.shtml
13 Ιαν 2014 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Θέλετε να παίξουμε ένα έξυπνο παιχνίδι; Παίζοντας το θα ανακαλύψετε πόσο έξυπνος είναι ο υπολογιστής σας, ότι μπορεί να καταλαβαίνει τι σκέφτεστε και ότι υπάρχουν μαγικά κόλπα…
Ας δούμε όμως πώς παίζεται.
Αρχικά πατάτε εδώ στο σπιτάκι 
και ακολουθείτε τις παρακάτω οδηγίες πατώντας 
:
1)Βλέπετε έναν πίνακα με αριθμούς. Πρέπει να διαλέξετε έναν από αυτούς π.χ. 
. Μην τον πείτε σε κανέναν, μόνο σκεφτείτε τον με το μυαλό σας.
2)Παρατηρήστε το χρώμα του αριθμού σας και επιλέξτε το ίδιο χρώμα στη γραμμή με τα χρώματα, που ακολουθεί π.χ. 
. Απομνημονεύστε τον αριθμό σας.
3)Τώρα πρέπει να διαλέξετε ένα από τα παρακάτω χρώματα. 
Διαλέξτε αυτό που σας αρέσει.
4)Μια σειρά από σπιτάκια περιέχουν αριθμούς, έξι διαφορετικούς αριθμούς το καθένα. Βρείτε σε ποιο σπιτάκι βρίσκεται ο αριθμός σας και επιλέξτε το 
.
5)Λίγα μαγικά …. πατήστε πάνω σε μία μπάλα…. Προσέξτε μη μαρτυρήσετε τον αριθμό σας, μην τον πείτε πουθενά. Το μηχάνημα σας ….ίσως σας ακούει …… ίσως λαμβάνει τη σκέψη σας ……ίσως
.
6)Βλέπετε τρεις πόρτες 
Πατήστε πάνω σε μία από αυτές. Μήπως είναι ο δικός σας αριθμός μέσα; Πώς έγινε αυτό;
Ωραία περάσαμε, παίξαμε και ξαφνιαστήκαμε με τα … μαγικά. Μήπως όμως πίσω από όλα αυτά κρύβονται τα μαθηματικά; Μήπως μπορούμε να δώσουμε μια εξήγηση; Πώς λειτουργεί το παιχνίδι;
Εναλλακτικά μπορείτε να παίξετε ΕΔΩ
Ο καθένας μας μπορεί να φτιάξει ένα δικό του παιχνίδι και να παίξει με τους φίλους του, προβληματίζοντας τους αρκετά με το πώς βρίσκουμε τον αριθμό που έχουν επιλέξει …
9 Ιαν 2014 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Πρόσφατα ασχοληθήκαμε στο μάθημα μας με το παρακάτω πρόβλημα του σχολικού βιβλίου.
Ακούστηκαν ενδιαφέρουσες ιδέες αλλά και νέα ερωτήματα, τα οποία σας μεταφέρουμε.
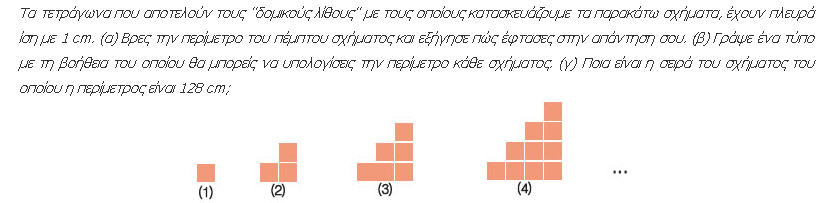
Το πρώτο ερώτημα με το οποίο ασχολήθηκαν οι μαθητές ήταν η εύρεση της περιμέτρου του 5ου σχήματος. Είχαν παρατηρήσει ότι καθένα σχήμα προκύπτει από το προηγούμενο αν στα δεξιά του προσθέσουμε μία νέα στήλη τετραγώνων με ένα τετράγωνο παραπάνω. Εύκολα και γρήγορα κατασκεύασαν το 5ο σχήμα και βρήκαν τη περίμετρο του,
Π_5 = 20 cm.
Σύμφωνα με το ερώτημα που ακολουθούσε έπρεπε να βρουν τον τύπο που υπολογίζει τη περίμετρο κάθε σχήματος, οπότε αποφάσισαν ότι έπρεπε να βρουν και τις περιμέτρους των προηγούμενων σχημάτων. Τα αποτελέσματα αυτά γράφτηκαν στον πίνακα:
Π1=4cm, Π2=8cm, Π3=12cm, Π4=16cm, Π5=20cm .
Εξήγησαν ότι βλέπουν ένα γεωμετρικό μοτίβο στο σχεδιασμό τους, αλλά και στις τιμές των περιμέτρων τους ένα άλλο αριθμητικό.
Ο μαθητής Σ. είπε ότι σύμφωνα με τους παραπάνω υπολογισμούς κάθε περίμετρος σχήματος διαφέρει από την περίμετρο του προηγούμενου κατά 4 και κατέληξε ότι:
Π_τυχαίου = Π_προηγούμενου + 4
Η μαθήτρια Κ. είπε ότι οι αριθμοί αυτοί είναι πολλαπλάσιοι του 4 άρα
Π_ν= 4 ν, όπου ν είναι ο αριθμός τετραγώνων της κάτω σειράς.
Ο μαθητής Ν. είπε ότι στα προηγούμενα σχήματα παρατηρεί το εξής: Π_1=4, Π2= 2+2+4=4 *2, Π_3=3+3+6 = 4 *3, Π_4 = 4+4+8 = 4*4 άρα
Π_ν = ν +ν +2ν =4ν (δείχνοντας τον αριθμό τετραγώνων περιμετρικά στα σχήματα)
Ο μαθητής Β. είπε ότι οι περίμετροι των σχημάτων αυτών συμπεριφέρονται όπως οι περίμετροι των τετραγώνων πλευράς ν. Η τεθλασμένη τους γραμμή μοιάζει σαν να είναι “τσαλακωμένη” από τις δύο πλευρές.
Ο μαθητής Δ. είπε ότι η “σκαλωτή” πλευρά τους ισούται με τη βάση επί 2 (νέο μοτίβο!)
Μπορείς να πειραματιστείς με το αρχείο που ακολουθεί για να διαπιστώσεις τα παραπάνω κι εσύ.
ΠΑΤΗΣΕ ΕΔΩ ή στην εικόνα: 
Στη συνέχεια ήρθε μια σειρά από νέα ερωτήματα των παιδιών, τα οποία αποτελούν πρόκληση για τον καθένα μας.
1)Αν προσθέσουμε στη κορυφή ενός σχήματος ένα ακόμη τετράγωνο, πόσο θα είναι η περίμετρος του νέου σχήματος;
2)Υπάρχει τύπος για τα εμβαδά των παραπάνω σχημάτων;
Μία υπόδειξη του μαθητή Β. Κ.
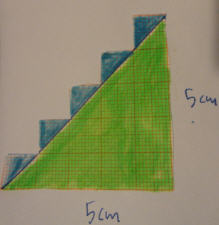
Από το παραπάνω σχήμα βλέπουμε ότι το εμβαδόν του σχήματος με βάση 5 τετράγωνα ισούται με Ε= (5^2/2 )+(5 /2) = (5^2+5)/2
άρα το όμοιο σχήμα με αυτό που έχει ν τετράγωνα στη βάση έχει εμβαδόν
Ε= (ν^2+ν)/2
Μία υπόδειξη του μαθητή Δ. Β.
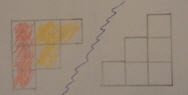
Προσθέτουμε άλλο ένα σχήμα ίδιο με αυτό που έχουμε ( το σχήμα έχει 3 τετράγωνα στη βάση) αλλά αναποδογυρισμένο σε σχέση με το πρώτο και τότε έχουμε ένα ορθογώνιο με μήκος 4 τετράγωνα και ύψος 3
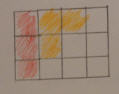
Το εμβαδόν του δεύτερου σχήματος είναι 3χ4 άρα το εμβαδόν του αρχικού σχήματος είναι 3χ4/2
επομένως το εμβαδόν ενός όμοιου σχήματος που έχει ν τετράγωνα στη βάση είναι:
Ε= ν (ν+1) /2
3) Πόσο είναι το άθροισμα των αριθμών 1+2+3+4+5 =;
1+2+3+4+… +ν=;
Μία υπόδειξη: Παρατήρησε ότι το εμβαδόν του σχήματος της προηγούμενης ερώτησης με 5 τετράγωνα στη βάση ισούται με 1+2+3+4+5.
4)Μετά τη συνεδρίαση και τα 10 μέλη του διοικητικού συμβουλίου μιας εταιρείας ανταλλάσσουν μεταξύ τους χειραψίες. Πόσες χειραψίες γίνονται συνολικά;
Μία υπόδειξη: Ας υποθέσουμε ότι ένας-ένας χαιρετάει τους υπόλοιπους και φεύγει. Τότε ο πρώτος θα ανταλλάξει συνολικά 9 χειραψίες, ο δεύτερος 8, ο τρίτος 7, ο τέταρτος 6, ο πέμπτος 5, ο έκτος 4, ο έβδομος 3, ο όγδοος 2, ο ένατος 1 και ο δέκατος καμία. Επομένως ο συνολικός αριθμός χειραψιών θα είναι 9+8+7+6+5+4+3+2+1=;
Πόσες χειραψίες θα ανταλλάξουν 100 μέλη ενός άλλου διοικητικού συμβουλίου; ν μέλη;
7 Ιαν 2014 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Ένας γρίφος για μικρούς και μεγάλους.
Τέσσερα διαφορετικά κομμάτια σχηματίζουν διάφορα σχέδια, όπως αυτό του σχήματος παρακάτω. Παίξε κι εσύ και σχημάτισε δικά σου σχέδια χρησιμοποιώντας κάθε φορά τα τέσσερα αυτά κομμάτια.
Προσπάθησε να κατασκευάσεις το κεφαλαίο γράμμα ΤΑΥ. Μετά απάντησε στο ερώτημα: Ποιο είναι το εμβαδόν του σχήματος που σχηματίζεται κάθε φορά από τα τέσσερα αυτά κομμάτια;
Κάνε κλικ πάνω στην εικόνα για να ανοίξεις το αρχείο (geogebra)
31 Δεκ 2013 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Καλή χρονιά με υγεία και χαρές σε όλους!
Το νέο έτος 2014 ας φέρνει σε όλους μας
ευημερία, ευτυχία και
μικρές χαρούμενες στιγμές στη κάθε ημέρα του.
Ανοίξτε το δώρο μιας φίλης μου, είναι ένα κουτί που έχει μέσα πρώτους αριθμούς;
Τι άλλο όμως κρύβει;
28 Δεκ 2013 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
10 Δεκ 2013 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
Η έκθεση ήταν εκπληκτική και πολύ ενδιαφέρουσα. Μου άρεσαν πολύ τα εκθέματα στο τραπέζι με τα γεωμετρικά σχήματα και το έκθεμα με τα 7 φωτάκια που όταν πατούσες το κουμπί σε ένα από αυτά άλλαζε η κατάσταση του (αναμμένο-σβηστό) καθώς και η κατάσταση στα αμέσως διπλανά του (δεξιά και αριστερά του). ΄Επρεπε να ανάψουμε όλα τα φωτάκια. Μετά από δοκιμές και πατατηρήσεις βρήκαμε το κόλπο να τα ανάβουμε όλα και το καταχαρήκαμε.
“Περικλής Λ.”
27 Νοέ 2013 από ΚΑΛΛΙΟΠΗ ΑΡΔΑΒΑΝΗ
O κύκλος του νερού — γνωστός και ως υδρολογικός κύκλος — είναι η αδιάκοπη κίνηση του νερού από την ατμόσφαιρα στην επιφάνεια της γης, στο υπέδαφος, στην υδρόσφαιρα και πάλι στην ατμόσφαιρα. Αυτό το φαινόμενο οφείλεται στην ηλιακή ακτινοβολία.
Ο κύκλος του νερού
ααα
Ο κύκλος του νερού από την εκπαιδευτική τηλεόραση:
ααα
Υπάρχουν παγωμένα ποτάμια;
![tuktoyaktuk-ice-road4[3]](https://blogs.sch.gr/popiardv/files/2013/11/tuktoyaktuk-ice-road43.jpg)
![tuktoyaktuk-ice-road10[2]](https://blogs.sch.gr/popiardv/files/2013/11/tuktoyaktuk-ice-road102.jpg)
Πηγή http://www.amusingplanet.com/2011/01/ice-road-to-tuktoyaktuk.html
ααα
Καλλιτεχνικές δημιουργίες στον πάγο – ή με πάγο:
ααα
Υπάρχουν “παγωμένες” πόλεις;
ααα
Παγόβουνα από Ανταρκτική
Παγόβουνα από την Ανταρκτική
ααα
Περισσότερα για τον κύκλο του νερού εδώ: USGS
ααα
ααα