- Βήμα 1: Σχεδιάζουμε ένα ισόπλευρο τρίγωνο ΑΒΓ
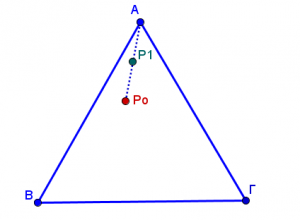
- Βήμα 2: Επιλέγουμε ένα τυχαίο σημείο στο εσωτερικό του τριγώνου ΑΒΓ και το ονομάζουμε Ρο.
- Βήμα 3: Ρίχνουμε το ζάρι και αν ο αριθμός είναι 1 ή 2 ενώνουμε το σημείο Ρο με το Α και παίρνουμε ως επόμενο σημείο το μέσο Ρ1 του τμήματος ΑΡο. Αν το ζάρι δείξει 3 ή 4 παίρνουμε το Ρ1 μέσο του ΒΡο. Αν το ζάρι δείξει 5 ή 6 παίρνουμε το Ρ1 μέσο του ΓΡο.
Εικόνα 1: Έστω ότι φέραμε 1 στη πρώτη ρίψη του ζαριού.
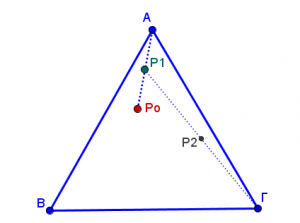
- Βήμα 4: Επαναλαμβάνουμε το βήμα 3 με το σημείο Ρ1 και βρίσκουμε ένα νέο επόμενο σημείο Ρ2.
Εικόνα 2: Έστω ότι φέραμε 5 στη δεύτερη ρίψη του ζαριού.
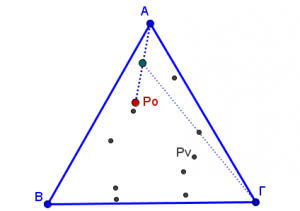
- Βήμα 5: Συνεχίζουμε επαναλαμβάνοντας την προηγούμενη διαδικασία πολλές φορές για κάθε επόμενο σημείο Ρν που προκύπτει ρίχνοντας κάθε φορά το ζάρι.
Κάθε φορά σβήνουμε το τμήμα που σχεδιάσαμε και κρατάμε στο σχήμα μας το Ρο και τα μέσα Ρ1, Ρ2, Ρ3, … Ρν των τμημάτων.
Εικόνα 3: Το σχήμα μας μετά από μερικές ρίψεις
- Βήμα 6: Αν Ρίξουμε το ζάρι πολλές φορές περιμένετε ότι θα προκύψει ένα σχήμα και αν ναι ποιο νομίζετε ότι θα είναι αυτό;
- Βήμα 7:Ας συνεχίσουμε το παιχνίδι αρκετές φορές για να διαπιστώσουμε το σχήμα που προκύπτει. Υπομονή: πρέπει να ρίξουμε το ζάρι 100 φορές ή μήπως 1000 ; Ίσως λίγο περισσότερες ;
- Βήμα 8: Ποιο σχήμα προέκυψε; Στην εικόνα που βρήκαμε επικρατεί η τάξη ή η αταξία;
- Βήμα 9: Μερική απάντηση ή περισσότερος προβληματισμός ;
Εφ όσον ρίχνουμε το ζάρι σε κάθε μας βήμα θα μπορούσε να πει κανείς ότι το Α, Β ή Γ που κινούμαστε κάθε φορά είναι τυχαίο. Επομένως τα σημεία Ρν που προκύπτουν από τη διαδικασία αυτή θα περίμενε κανείς τελικά να διασκορπίζονται ομοιογενώς μέσα στο τρίγωνο, γεμίζοντας το όλο καθώς το ν αυξάνει συνεχώς.
Ας σκεφτούμε όμως και κάτι άλλο : Από τη στιγμή που έχουμε ρίξει το ζάρι η κίνηση μας είναι απόλυτα προσδιορισμένη. Κατευθυνόμαστε προς ένα από τρία σημεία του επιπέδου και σταματάμε ακριβώς στη μέση της απόστασης μας από αυτό. Άρα κάθε φορά κάνουμε κάτι πολύ συγκεκριμένο . Ποιος θα νικήσει λοιπόν στην περίεργη διελκυστίνδα ανάμεσα στον ντετερμινισμό και στην τυχαιότητα; Θα επικρατήσει τελικά η αταξία ή θα εμφανιστεί κάποια τάξη στην εικόνα που θα προκύψει;
Αναμένεται απάντηση από τους μαθητές.
- Βήμα 10: Το αποτέλεσμα μήπως είναι αναμενόμενο; Έχουμε κάποια εξήγηση;
Πηγή: Τάσος Μπούντης ” Ο θαυμαστός κόσμος των Fractal”