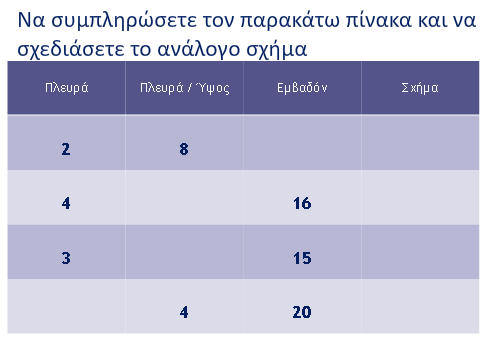
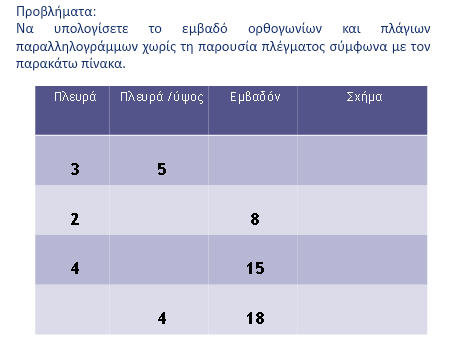
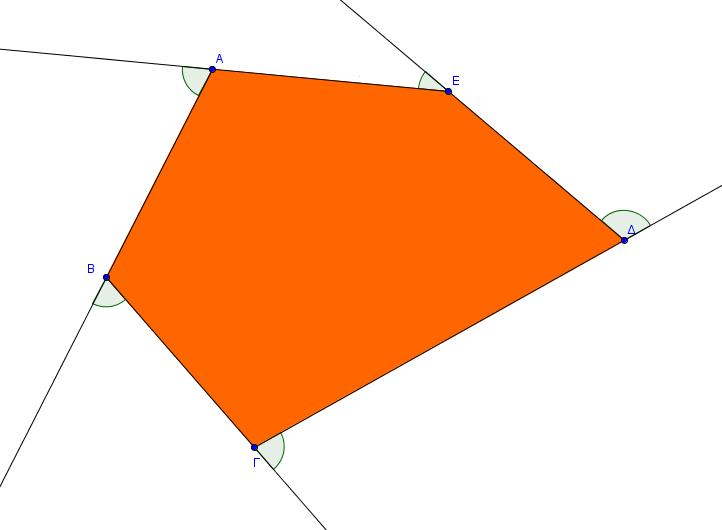
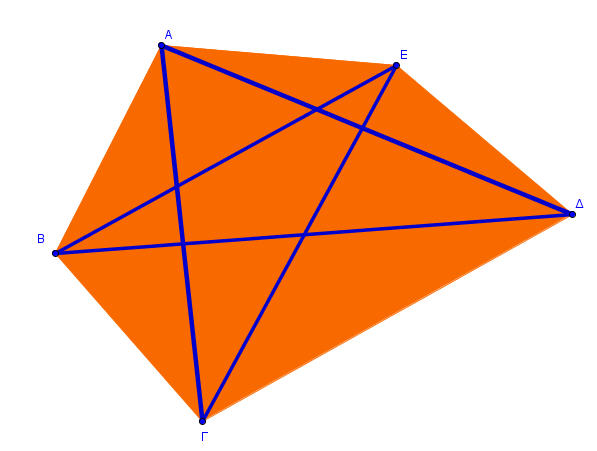
ΕΡΓΑΣΙΑ:
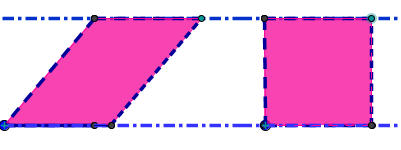
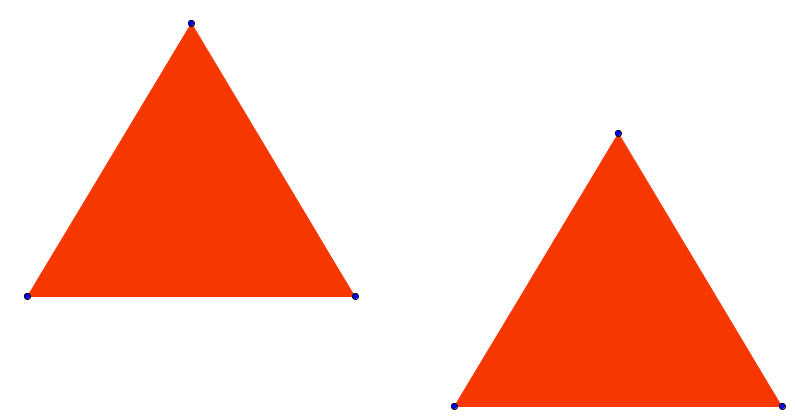
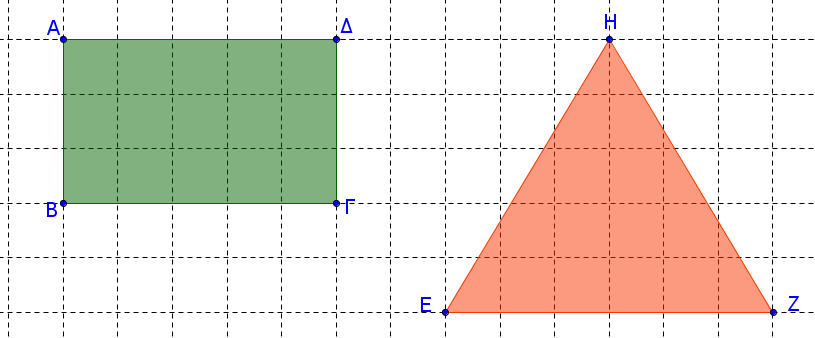
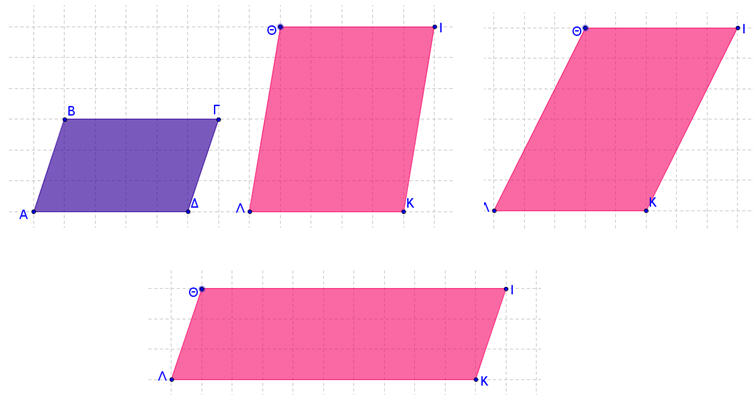
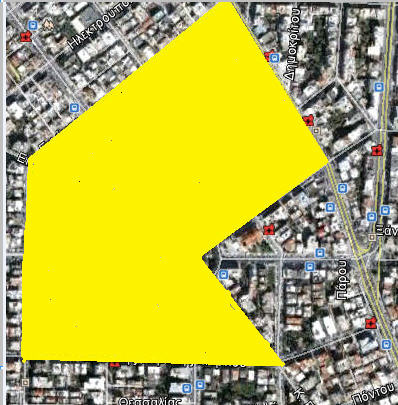
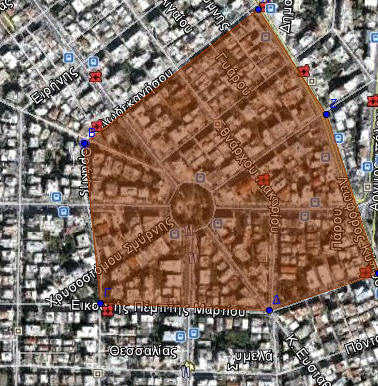
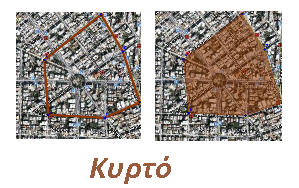
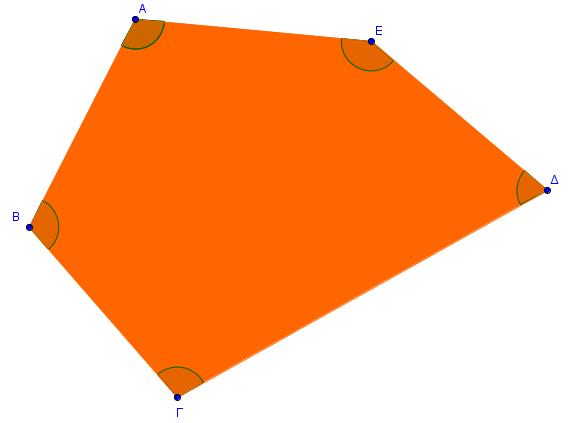
Α) Μπορείτε να ομαδοποιήσετε τα παρακάτω πολύγωνα σε δύο κατηγορίες;
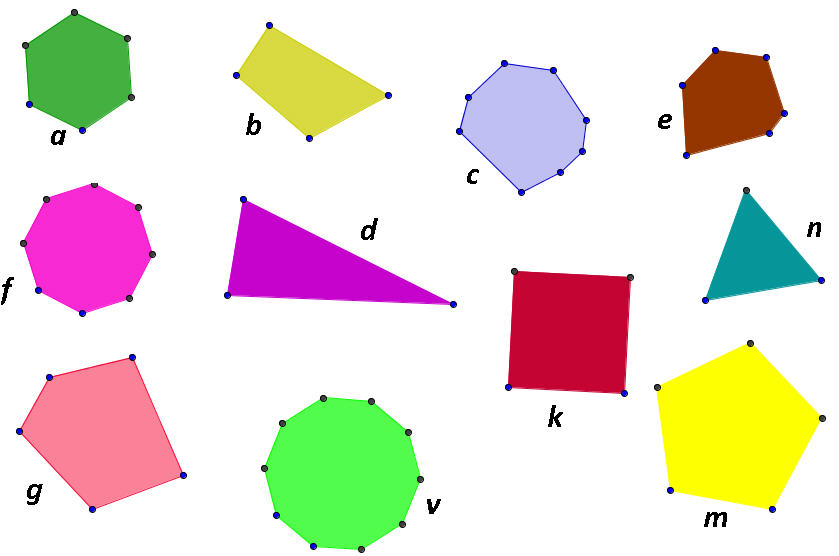
Β) Ποιο ήταν το κριτήριο σας στη παραπάνω ομαδοποίηση;
Γ) Ταξινομήστε τα γνωστά σας τετράπλευρα (τραπέζιο, παραλληλόγραμμο, ορθογώνιο, ρόμβος, τετράγωνο) στις δύο κατηγορίες πολυγώνων, που δημιουργήσατε πριν.
Αυτά τα ερωτήματα μας απασχόλησαν στο μάθημα.
Οι μαθητές πρότειναν τον διαχωρισμό τους σε πολύγωνα
α) με αριθμό πλευρών < 6 και αριθμό πλευρών >5
β) σε πολύγωνα που έχουν ίσες ή όχι πλευρές.
γ)σε πολύγωνα που έχουν ίσες ή όχι πλευρές και γωνίες.
δ) σε κυρτά και μη κυρτά.
Ο τελευταίος διαχωρισμός αποφάσισαν ότι ήταν άστοχος αφού όλα τα πολύγωνα του παραπάνω σχήματος είναι κυρτά. Στη κουβέντα που ακολούθησε είπαν ότι από όλες τις παραπάνω προτεινόμενες κατηγορίες έχει ενδιαφέρον να εξετάσουμε τα πολύγωνα που έχουν ίσες πλευρές και ίσες γωνίες. Αυτά μπορεί να έχουν και περισσότερες ιδιότητες, όπως άξονες συμμετρίας κλπ.
ΚΑΝΟΝΙΚΑ ΠΟΛΥΓΩΝΑ
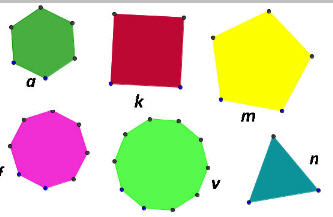
Ονομάσαμε κανονικό πολύγωνο, το πολύγωνο που έχει όλες τις πλευρές του μεταξύ τους ίσες και όλες τις γωνίες του μεταξύ τους ίσες. Τέτοια πολύγωνα είναι το ισόπλευρο τρίγωνο, το τετράγωνο, το κανονικό πεντάγωνο, το κανονικό εξάγωνο κλπ
ΚΑΤΑΣΚΕΥΗ ΚΑΝΟΝΙΚΟΥ ΠΟΛΥΓΩΝΟΥ
Φτιάξαμε ένα κύκλο στο τετράδιο μας και μας ζητήθηκε να τοποθετήσουμε 5 σημεία σε αυτόν ώστε να κατασκευάσουμε ένα κανονικό πεντάγωνο, ένα πεντάγωνο με όλες τις πλευρές και όλες τις γωνίες του ίσες. Μερικοί μαθητές ξεκινήσαμε βάζοντας 5 σημεία στο κύκλο με το μάτι.
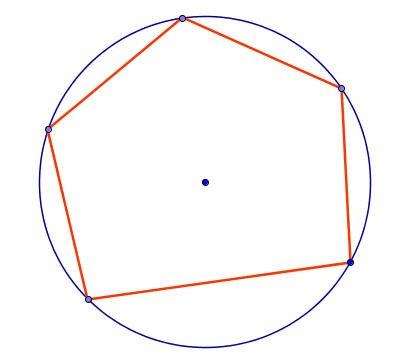
Η καθηγήτρια μας είπε να είναι ακριβής η κατασκευή μας οπότε ξεκινήσαμε από ένα σημείο Α του κύκλου και συνεχίσαμε με τη βοήθεια του διαβήτη και του χάρακα να σχεδιάζουμε ίσες χορδές. Η ιδέα μας ήταν εξαιρετική αλλά η τελευταία πλευρά δεν ήταν ίση με όλες τις άλλες… Τι έπρεπε να κάνουμε;
-Η καθηγήτρια μας είπε να σκεφτούμε τι ακριβώς θέλουμε να κάνουμε.
–Θέλουμε να είναι όλες οι πλευρές ίσες.
-Μας ρώτησε ποια άλλα στοιχεία στο σχήμα τότε θα είναι ίσα;
-Σκεφτήκαμε ότι θέλουμε όλες οι πλευρές να είναι ίσες άρα και τα αντίστοιχα τόξα και τότε καταλάβαμε ότι πρέπει να χωρίσουμε τον κύκλο σε 5 ίσα τόξα.Αυτό είναι εύκολο κάθε τόξο θα έχει άνοιγμα 36Ο / 5 = 72 μοίρες!
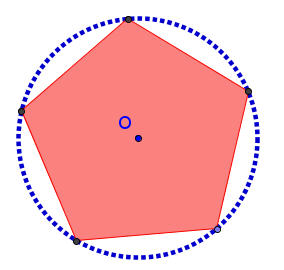
Οπότε ξαναπροσπαθήσαμε τη κατασκευή κανονικού πενταγώνου και διαπιστώσαμε ότι πέτυχε! Ξεκινήσαμε από ένα σημείο του κύκλου και μετρούσαμε τώρα επίκεντρες γωνίες 72 μοιρών. Ετσι κατασκευάσαμε ένα κανονικό πεντάγωνο. Πράγματι όλες οι πλευρές του είναι τώρα ίσες αφού αντιστοιχούν σε ίσα τόξα 72 μοιρών, όσο και η αντίστοιχη επίκεντρη γωνία, αλλά και οι γωνίες του είναι ίσες και μάλιστα 108 μοιρών η κάθε μία, ως εγγεγραμμένη σε τόξο 3* 72 = 216 μοιρών. Με παρόμοιο τρόπο θα μπορούσαμε να κατασκευάσουμε ένα οποιοδήποτε κανονικό πολύγωνο!
ΠΕΡΙΓΓΕΓΡΑΜΜΕΝΟΣ ΚΥΚΛΟΣ
Σύμφωνα με τη προηγούμενη διαδικασία κατασκευάζουμε ένα κανονικό πολύγωνο του οποίου οι κορυφές είναι σημεία ενός κύκλου.Ο κύκλος αυτός ονομάζεται περιγγεγραμμένος κύκλος του κανονικού πολυγώνου.
ΚΕΝΤΡΙΚΗ ΓΩΝΙΑ ΚΑΝΟΝΙΚΟΥ ΠΟΛΥΓΩΝΟΥ

Η επίκεντρη γωνία που μας οδήγησε στη κατασκευή του κανονικού πενταγώνου είναι ένα ιδιαίτερο στοιχείο του κανονικού πολυγώνου. Ορίζουμε κεντρική γωνία του κανονικού ν-γωνου την επίκεντρη γωνία ω = 360/ν μοίρες.
ΓΩΝΙΑ ΤΟΥ ΚΑΝΟΝΙΚΟΥ ΠΟΛΥΓΩΝΟΥ

Ας προσπαθήσουμε να προσδιορίσουμε τη γωνία ενός κανονικού πολυγώνου. Από τα ισοσκελή τρίγωνα που σχηματίζονται σε οποιοδήποτε κανονικο πολύγωνο έχουμε φ/2 + φ/2 + ω = 180 μοίρες ή φ+ω=180 μοίρες.
φ =180 – ω
Στη συνέχεια κάναμε δύο εφαρμογές των παραπάνω τύπων για να βρούμε α)τη γωνία ενός κανονικού δεκαγώνου και β) το κανονικό πολύγωνο που έχει γωνία 162 μοιρών.
Ενας μαθητής παρατήρησε
–κα όσο αυξάνεται ο αριθμός των πλευρών ενός κανονικού πολυγώνου μεγαλώνει και η γωνία του; –η καθηγήτρια σχημάτισε με τα δύο της χέρια τη γωνία 60 μοιρών του ισοπλεύρου τριγώνου και τα άνοιγε κάθε φορά περισσότερο για να αναπαραστησει τη γωνία τετραγώνου, κανονικού πενταγώνου κλπ. Πράγματι για μεγάλο αριθμό πλευρών αντιστοιχεί μεγάλη γωνία.
Αρα γε ποια σχέση μπορεί να συνδέει αυτά τα δύο ποσά;
Μήπως υπάρχει σχέση, η οποία να συνδέει τον αριθμό πλευρών με τη κεντρική γωνία του κανονικού πολυγώνου και ποια είναι αυτή;
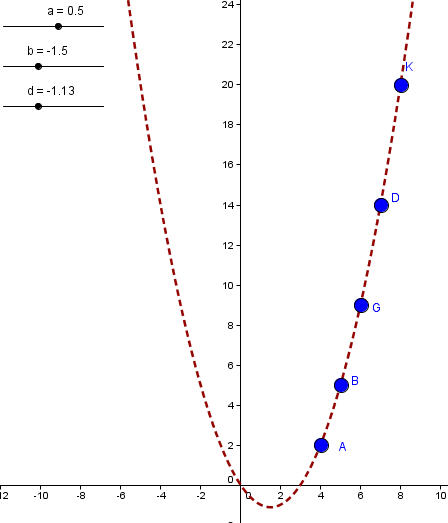
Θα πρέπει να παραστήσουμε σημεία στο επίπεδο με τη σχέση: (ν , 180-ω) =(ν , 180 – 360/ν)
και με τη σχέση (ν , ω) =(ν , 360/ν).
Με τη χρήση του λογισμικού Geogebra και τη βοήθεια δρομέα ν δίνοντας τιμές σε αυτόν από 3 έως 20 και με βήμα 1 μπορούμε να έχουμε όλα αυτά τα σημεία και να παρατηρήσουμε τη σχέση τους.
Αν δυσκολευόμαστε με το λογισμικό ας το δοκιμάσουμε: ΕΔΩ.