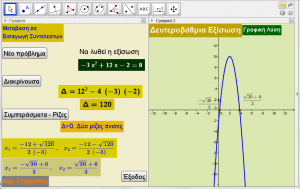
Το αρχείο που δημοσιεύουμε παρουσιάζει την λύση της δευτεροβάθμιας εξίσωσης σε διαδοχικά βήματα.
Ο χρήστης μπορεί να επιλέξει μεταξύ του να εισάγει συγκεκριμένη εξίσωση για μελέτη, ή να αφήσει τον υπολογιστεί να επιλέξει μία (τυχαία).

Με αφορμή το πρόβλημα της επίλυσης της δευτεροβάθμιας εξίσωσης, αναδεικνύουμε την δυνατότητα που έχουν οι νεότερες εκδόσεις Geogebra, με κατάλληλες εντολές κειμένου, να εκτελούν αντικαταστάσεις σε δεδομένο τύπο (αναλυτικά) και στη συνέχεια να τον απλοποιούν.
Το αρχείο μπορεί να χρησιμοποιηθεί για την διδασκαλία στην Γ΄ Γυμνασίου αλλά και την Α΄ Λυκείου.

Για να κατεβάσετε το αρχείο πατήστε επάνω στην εικόνα.

Μια τριγωνομετρική συνάρτηση, λίγες ελείψεις, μερικά κείμενα και  κουμπιά ελέγχου, τα υλικά για την Πασχαλινή μας κάρτα.

Τις ευχές μας για καλή Ανάσταση!

Με αφορμή μια άσκηση του σχολικού βιβλίου της Β΄ Γυμνασίου, στην ενότητα «Μέτρηση κύκλου-τόξου», δημιουργήθηκε το αρχείο αυτό που δίνει μα αναπαράσταση του προβλήματος.

Μπορεί να διδαχθεί και στην Β΄ Λυκείου. Με το κουμπί «Βοήθεια» δίνεται η δυνατότητα επίδειξης του τρόπου κατασκευής της κοινής εφαπτομένης δύο κύκλων, και αφήνεται στο διδάσκοντα να επιλέξει αν θα το διδάξει.
Στην κατασκευή του αρχείου χρησιμοποιήθηκαν οι εντολές ΔείξεΣτρώση[ ] και ΑπόκρυψηΣτρώσης[ ] του λογισμικού.

Για να κατεβάσετε το αρχείο πατήστε επάνω στην εικόνα.

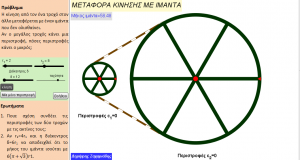
Δημοσιεύουμε την εισήγηση με θέμα:  «Ο Μηχανισμός των Αντικυθήρων. Μία διδακτική προσέγγιση» που παρουσιάστηκε στο ετήσιο συνέδριο της Ελληνικής Μαθητικής Εταιρείας που πραγματοποιήθηκε από 8 έως 10/11/2013 στην Καρδίτσα. Η εισήγηση συνοδευόταν από 6 αρχεία του λογισμικού Geogebra με τους παρακάτω τίτλους:

• Μεταφορά κίνησης από γρανάζι σε γρανάζι (εμπλοκή δύο γραναζιών,  εμπλοκή τριών γραναζιών).
• Μετάδοση κίνησης σε συρμό τεσσάρων γραναζιών.
• Ο συρμός της Σελήνης.
• Το σύστημα Πίρος – Σχισμή.
• Επικυκλική τοποθέτηση γραναζιών.
• Ψηφιακό ομοίωμα του Μηχανισμού των Αντικυθήρων.

Με την παραπάνω εργασία γίνεται προσπάθεια να κατανοηθεί, ακόμα και από τους μη ειδικούς, η λειτουργία του Μηχανισμού. Η εισήγηση που δημοσιεύουμε περιλαμβάνεται ως κείμενο στα πρακτικά που εξέδωσε η ΕΜΕ, αλλά όχι και τα αρχεία Geogebra, ούτε βέβαια το σχετικό PowerPoint της παρουσίασης που αποτελούν ίσως το πιο ενδιαφέρον εποπτικό υλικό. Με τη δημοσίευση αυτή δημοσιεύουμε ένα μέρος από αυτό το υλικό και όταν είναι έτοιμο θα δημοσιευτεί και το υπόλοιπο.

Το εποπτικό υλικό αυτό παρουσιάστηκε από εμένα στα παρακάτω σχολεία που με τίμησαν με πρόσκληση τους.

• Πρότυπο Πειραματικό Λύκειο Μυτιλήνης  4/12/2013 Α΄ Λυκείου
• Πρότυπο Πειραματικό Λύκειο Μυτιλήνης  4/12/2013 Β΄ Λυκείου
• Πρότυπο Πειραματικό Λύκειο Αναβρύτων 9/12/2013 Α΄ Λυκείου
• Πρότυπο Πειραματικό Λύκειο Ευαγγελικής Σχολής Σμύρνης                           24/1/2014 Α΄ Λυκείου

Στη σημερινή δημοσίευση εκτός από την εισήγηση στην ΕΜΕ δημοσιεύουμε σε πρώτη φάση και δύο από τα αρχεία Geogebra:

• Μεταφορά κίνησης από γρανάζι σε γρανάζι (εμπλοκή δύο γραναζιών,  εμπλοκή τριών γραναζιών).
• Μετάδοση κίνησης σε συρμό τεσσάρων γραναζιών.

Για να μεταφορτώσετε τα αρχεία κάνετε κλικ επάνω στην εικόνα.

Δημήτρης Ζαχαριάδης

Στο μάθημα αυτό περιγράφεται ένας διαφορετικός τρόπος (στο 30ο βιντεομάθημα είχαμε κάνει μια πρώτη παρουσίαση για στερεά στο Geogebra)  για το πως μπορούμε να δημιουργήσουμε ένα στερεό στην επιφάνεια του Geogebra και να μελετήσουμε τις ιδιότητες του.

Για να μεταφορτώσετε το αρχείο Geogebra που δημιουργήθηκε κάνετε κλικ εδω.

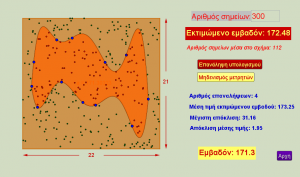
Ας υποθέσουμε ότι θα επιθυμούσαμε να υπολογίσουμε το εμβαδόν μιας επίπεδης μορφής για την οποία δεν υπάρχει κανένας τύπος που να την υπολογίζει επακριβώς. Υπάρχουν αρκετές μέθοδοι για να μπορέσουμε να το εκτιμήσουμε, όμως μια από τις πιο διασκεδαστικές είναι η ονομαζόμενη μέθοδος Monte Carlo που βασίζεται στις εαναλαμβανόμενες τυχαίες δειγματοληψίες. Η ιδέα είναι απλή: αρκεί να περιγράψουμε τη συγκεκριμένη μορφή με ένα ορθογώνιο του οποίου το εμβαδόν υπολογίζεται εύκολα, και στη συνέχεια να δημιουργήσουμε έναν αριθμό τυχαίων σημείων μέσα στο ορθογώνιο (π.χ. κρεμώντας το όλο σχήμα στον τοίχο και ρίχνοντας πάνω του βελάκια χωρίς να σημαδεύουμε)… Τότε αν δημιουργήσαμε 100 τέτοια σημεία μέσα στο ορθογώνιο, και από αυτά τα 60 κατέληξαν να είναι μέσα στην «περίεργη» μορφή, τότε το εκτιμώμενο εμβαδόν θα αντιστοιχεί στο 60% του εμβαδού του ορθογωνίου. Η συγκεκριμένη εφαρμογή αναπαριστά αυτή τη μέθοδο εκτίμησης εμβαδού, αλλά επιπλέον δείχνει και μια εφαρμογή της συγκεκριμένης μεθόδου στον υπολογισμό του π.

Θα μπορούσε να διδαχθεί στο μάθημα των πιθανοτήτων τόσο στην Α’, όσο και στα Μαθηματικά Γενικής Παιδείας στη Γ’ Λυκείου.

Για να μεταφορτώσετε το αρχείο κάνετε κλικ επάνω στην εικόνα.

Από ένα πρόβλημα που έβαλε αγαπημένη γραφίστρια: «Πώς μπορούμε να σχεδιάσουμε 15 κύκλους που να εφάπτονται ανά δύο και να εφάπτονται όλοι εξωτερικά σε δεδομένο κύκλο» προέκυψε η γενίκευση  που δημοσιεύουμε, που είναι ένα  πρόβλημα επικάλυψης ενός κύκλου με n κύκλους. Από διδακτική άποψη το ενδιαφέρον εστιάζεται στο γεγονός ότι δείχνει με απτό τρόπο πώς μπορούν να συνδυαστούν διάφορες περιοχές των Μαθηματικών στην επίλυση ενός προβλήματος· διότι για την θεωρητική επίλυση του δοθέντος προβλήματος, γίνεται χρήση τριγωνομετρίας (επίλυση τριγώνου), γεωμετρίας (ομοιότητα – σχετική θέση δύο κύκλων), άλγεβρας (πρόοδοι) και ανάλυσης (όριο ακολουθίας). Για το λόγο αυτό, η συγκεκριμένη εφαρμογή τοποθετήθηκε στην κατηγορία «ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ», αφήνοντας το διδάσκοντα να επιλέξει σε ποια τάξη θα επιθυμούσε να το παρουσιάσει, ανάλογα σε ποια(ες) πλευρά(ες) του προβλήματος θα ήθελε να επικεντρωθεί.

Για να κατεβάσετε την εφαρμογή κάνετε κλικ πάνω στην εικόνα.

Αναδημοσίευση ανάρτησης του προηγούμενου ιστολόγιου του Δημήτρη Ζαχαριάδη – blogs.sch.gr/dimzachari

Με την δημοσίευση αυτή ολοκληρώνεται η μεταφορά των μαθημάτων Geogebra από το παλιό ιστολόγιο στο νέο. Έως τώρα έχουν δημοσιεύθεί 33 βιντεομαθήματα και θα τα βρείτε όλα στο παρόν ιστολόγιο. Λόγω μεταφοράς η σειρά δημοσίευσης δεν είναι ενιαία.

Για να μάθει κανείς το geogebra θα πρέπει να παρακολουθήσει τα μαθήματα με αύξουσα σειρά.

Τα μαθήματα 1-23 είναι βιντεοσκοπημένα στο παλαιό περιβάλον του Geogebra και καλό είναι πριν τα δεί κάποιος να έχει μελετήσει το μάθημα 32 που εντοπίζονται οι κυριότερες διαφορές περιβάλοντος μεταξύ των εκδόσεων 3 και 4.

Αναδημοσίευση ανάρτησης του προηγούμενου ιστολόγιου του Δημήτρη Ζαχαριάδη – blogs.sch.gr/dimzachari

Αναδημοσίευση ανάρτησης του προηγούμενου ιστολόγιου του Δημήτρη Ζαχαριάδη – blogs.sch.gr/dimzachari