Βιβλιοπαρουσίαση
Ένας Κόσμος δίχως Χρόνο
Μετάφραση: Έλενα Πισσία,Εκδ. Τραυλός, σελ. 312
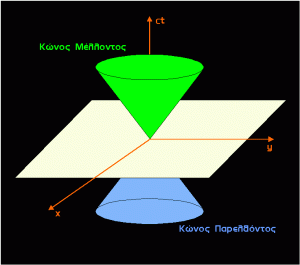
Ο τίτλος του κειμένου δείχνει με τρόπο σαφή την υπαρξιακή διάσταση της ενασχόλησης όλων των ανθρώπινων όντων με τον χρόνο. Παρμένο, μάλιστα, από ένα κείμενο σχετικό με την φιλοσοφία του Χάιντεγκερ, μεταφέρει την έγνοια του μεγάλου γερμανού διανοητή για το ζήτημα των ζητημάτων, αυτό το χρόνου, του πιο «αν-όριστου» από όλα τα σημαντικά –κι ίσως γι’ αυτό του πιο σημαντικού. Εμείς οι άνθρωποι, τα «εδώ –να –είναι» όπως μας λέει ο Χάιντεγκερ, είμαστε τόσο πολύ χρονικά όντα, τόσο εν χρόνω και τόσο τρομαγμένα από τον χρόνο, δηλαδή τον θάνατο, που ανεξαιρέτως φιλοσοφούμε με αυτό το αντικείμενο, ακόμη κι αν δεν το συνειδητοποιούμε. Κάποιοι, βέβαια, φιλοσοφούν καλύτερα και πιο συστηματικά από τους άλλους. Κι ας μην είναι κι αυτοί επαγγελματίες φιλόσοφοι, αλλά φυσικοί ή μαθηματικοί. Από ένα σημείο και ύστερα –ή από ένα σημείο και πριν;- κάτι τέτοιο γίνεται υποχρεωτικό. Αυτό συνέβη με τον Αϊνστάιν, ο οποίος με την Ειδική Θεωρία της Σχετικότητας πέτυχε ταυτόχρονα δύο πράγματα σε σχέση με την αντίληψη του χρόνου, που έμελλε να επαναφέρουν στο προσκήνιο, με μεγαλύτερη από ποτέ ένταση, αντινομίες πολύ δύσκολα διαχειρίσιμες και άρα φιλοσοφικά ιδιαίτερα διεγερτικές. Από τη μία, μετέτρεψε τον τρισδιάστατο χώρο σε τετραδιάστατο χωροχρόνο, το νέο τετραδιάστατο χώρο της σχετικότητας, δίνοντας στους φυσικούς τη δυνατότητα να χειρίζονται τον χρόνο ως γεωμετρικό αντικείμενο –κάτι, δηλαδή, απόλυτα στέρεο και μονοσήμαντο. Από την άλλη, με την ίδια κίνηση, έδειξε πως ο χρόνος μετριέται διαφορετικά ανάλογα με το σύστημα αναφοράς στο οποίο μετέχει ο παρατηρητής: αλλιώς ειπωμένο, ο χρόνος δεν είναι οικουμενικός κι απόλυτος, όπως πίστευε ο Νεύτωνας, αλλά τοπικά καθορισμένος και σχετικός. Π.χ., δύο γεγονότα που φαίνονται ταυτόχρονα σε έναν παρατηρητή, εμφανίζουν χρονική απόσταση μεταξύ τους για έναν άλλο που, απλώς, κινείται σχετικά με τον πρώτο –και μάλιστα ομαλά.
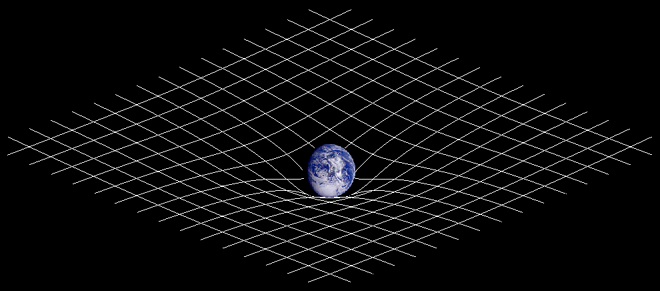
Και το κυριότερο: και οι δύο, κατά τον Αϊνστάιν, έχουν δίκιο. Αν είναι έτσι, όμως, -που είναι- ποιό είναι το ρολόι που μετράει τον «αντικειμενικό» χρόνο; Φανερά, τέτοιο ρολόι δεν υπάρχει, κανένα ρολόι σε ολόκληρο το σύμπαν δεν έχει το προνόμιο να μετράει «απόλυτα». Τότε, όμως, όπως ο καθένας κατανοεί, δύσκολα αποκτάει νόημα ο ισχυρισμός πως το σύμπαν ξεκίνησε την εξέλιξή του πριν από 13,7 δισεκατομμύρια χρόνια. Ποιό ρολόι τον μέτρησε αυτόν τον χρόνο; Η διατύπωση της Γενικής Θεωρίας της Σχετικότητας, που συνέδεσε ισχυρά το χωροχρόνο με την ύλη του σύμπαντος σε μια ενότητα, υποστηρίζοντας πως ο χωροχρόνος δεν συνιστά το δοχείο εντός του οποίου εξελίσσεται το σύμπαν, αλλά είναι το σύμπαν το ίδιο, έφερε σπουδαία προχωρήματα στην κατανόηση του κόσμου –και μαζί διατήρησε όλες τις σχετικές με τον χρόνο περιπλοκές. Τώρα πια δεν έχουμε μόνο σχετικότητα του χρόνου ως προς τους διαφορετικά κινούμενους αδρανειακούς παρατηρητές, αλλά προβλέψεις εξωτικότατες, όπως στρεβλώσεις και συστροφές τέτοιες, όταν οι συνθήκες είναι κατάλληλες, που μέχρι και για ταξίδια στο χρόνο μπορεί να προϊδεάσουν. Και όχι μόνο. Επιπλέον, ο χρόνος ως μέρος του σύμπαντος επεκτείνεται μαζί του. Αλλά τι σημαίνει πως ο χρόνος επεκτείνεται, αφού οποιαδήποτε επέκταση μόνο «μέσα στο χρόνο» μπορεί να συμβαίνει; Όπως το έθετε ο Αυγουστίνος, τι σημαίνει ότι ο χρόνος ρέει, με δεδομένο πως «ρέω» σημαίνει πως ρέω στον χρόνο;
* * * Το βιβλίο του Yourgrau ασχολείται με την πραγμάτευση του προβλήματος του χρόνου από τον Κουρτ Γκέντελ. Μια συνεισφορά καίρια και λησμονημένη για πολύ καιρό, από κάποιον που έκανε τις δυσκολίες μέρος της λύσης του προβλήματος. Ο Γκέντελ, όταν αποφάσισε να καταπιαστεί με το ζήτημα του χρόνου, είχε ήδη ολοκληρώσει δύο κολοσιαίες συνεισφορές στην επιστήμη. Διατύπωσε και απέδειξε το θεώρημα της μη πληρότητας, σύμφωνα με το οποίο κανένα τυπικό σύστημα, όπως π.χ. αυτό της αριθμητικής, δεν μπορεί να είναι πλήρες. Αποδιάρθρωσε έτσι τις φιλοδοξίες των μαθηματικών για τη δημιουργία ενός συστήματος, που θα παρήγαγε αποδεικτικά «όλες τις μαθηματικές αλήθειες του κόσμου», αποδεικνύοντας πως αυτό είναι αδύνατον. Επιπλέον, αναμετρήθηκε με επιτυχία με την «υπόθεση του συνεχούς», αποδεικνύοντας πως ο κόσμος του απείρου είναι τακτοποιημένος όσο κι αυτός των κοινών αριθμών. Ήδη από το δεύτερο μισό του 19ου αιώνα, ο Κάντορ είχε δείξει πως δεν πρέπει να μιλάμε για άπειρο, αλλά για άπειρα. Έδειξε, δηλαδή, πως υπάρχουν πολλά άπειρα, άλλα μικρότερα και άλλα μεγαλύτερα. Το μικρότερο άπειρο σε αυτήν την κατάταξη είναι αυτό που αντιστοιχεί στο πλήθος των φυσικών αριθμών. Η «υπόθεση του συνεχούς», που απέδειξε ο Γκέντελ, ισχυρίζονταν πως υπάρχει μια ορισμένη μαθηματική σχέση μεταξύ αυτού του «μικρότερου των απείρων» και του αμέσως μεγαλύτερου, που αντιστοιχεί στο πλήθος των σημείων μιας γραμμής, δηλαδή στο πλήθος των πραγματικών αριθμών. Ο Yourgrau επιχειρεί στο βιβλίο του να σπάσει τη «συνωμοσία της σιωπής» που περιβάλλει, όπως ισχυρίζεται, δεκαετίες τώρα μια από τις σημαντικότερες συμβολές όλων των εποχών στη διερεύνηση του ζητήματος του χρόνου. Εν συνόψει πρόκειται για το εξής: «Ο Γκέντελ, αυτός ο συνδυασμός Κάφκα και Αϊνστάιν, απέδειξε για πρώτη φορά στην ιστορία, χρησιμοποιώντας τις εξισώσεις της σχετικότητας, ότι τα ταξίδια στο χρόνο δεν ήταν μια φαντασίωση των φιλοσόφων αλλά μια επιστημονική πιθανότητα. Για μια ακόμη φορά, είχε καταφέρει, ξεκινώντας από τα τρίσβαθα των μαθηματικών, να ρίξει μια βόμβα στα χέρια των φιλοσόφων. Μόνο που το νέφος που ανασήκωσε αυτή η βόμβα ήταν πολύ πιο επικίνδυνο από αυτό που είχε ακολουθήσει το θεώρημα της μη πληρότητας. Ο Γκέντελ έσπευσε να επισημάνει πως, εάν μπορούμε να επισκεφτούμε το παρελθόν, αυτό σημαίνει πως δεν έχει πραγματικά «παρέλθει». Όμως, χρόνος που δεν περνάει δεν είναι χρόνος. Ο Αϊνστάιν κατάλαβε αμέσως ότι αν ο Γκέντελ είχε δίκιο, τότε δεν είχε απλώς εξημερώσει τον χρόνο: τον είχε σκοτώσει. Ο χρόνος, «αυτή η μυστηριώδης και φαινομενικά αυτοαναιρούμενη οντότητα», όπως έλεγε ο Γκέντελ, «που από την άλλη, μοιάζει να αποτελεί τη βάση της ύπαρξής μας και ολόκληρου του κόσμου μας», αποδεικνύεται τελικά η μεγαλύτερη ψευδαίσθηση» (σελ. 21). Είναι ευτύχημα, πραγματικά, που κάποιος σαν τον Γκέντελ ασχολήθηκε με το θέμα του χρόνου. Η μέθοδός του, όπως και στις προηγούμενες εργασίες του, ήταν η δημιουργία οριακών περιπτώσεων, τόσο ακραίων ώστε να «πιέζεται» η κατάσταση να δώσει καθαρή απάντηση. Τι έκανε, δηλαδή; Επιλέγοντας μια συγκεκριμένη κατανομή ύλης και κίνησης στο σύμπαν κατέληξε σε λύση των εξισώσεων Αϊνστάιν, που αντιστοιχούν σε ένα μοντέλο του κόσμου, όπου υπήρχαν διαδρομές, οι οποίες συνέδεαν κάθε ζεύγος γεγονότων έτσι ώστε, ακόμη κι όταν το Β παρατηρούνταν να συμβαίνει μετά το Α, μπορούσε κανείς ταξιδεύοντας με ένα πολύ γρήγορο διαστημόπλοιο να μεταβεί στο Β προτού φθάσει στο Α. Αυτές οι διαδρομές –που στην ορολογία της σχετικιστικής θεωρίας ονομάζονται κλειστές συνεχείς χρονοειδείς κοσμικές γραμμές- περιγράφουν με καθαρότητα ταξίδια στον χρόνο –στο μέλλον και στο παρελθόν. Όπως γράφει ο Yourgrau, «[o] Γκέντελ είχε καταφέρει να δείξει με θαυμαστό τρόπο ότι το ταξίδι στο χρόνο, με την αυστηρή σημασία του όρου, ήταν συνεπές με την θεωρία της σχετικότητας. Όσοι ενθουσιάζονται με την ιδέα του ταξιδιού στο χρόνο βρίσκουν αυτή την ανακάλυψη συναρπαστική, συχνά όμως δε βλέπουν ότι μια από τις συνέπειές της είναι το αδιάσειστο επιχείρημα ότι, αν είναι δυνατό το ταξίδι στο χρόνο, τότε ο ίδιος ο χρόνος δεν μπορεί να υπάρχει» (σελ. 168). Μόνο που, θα μπορούσε να πει ο προσεκτικός αναγνώστης, όλα αυτά αποδεικνύεται πως ισχύουν σε ένα εξαιρετικά ακραίο και προσεκτικά επιλεγμένο από τον Γκέντελ σύμπαν, όχι στο δικό μας, όπου ο χρόνος είναι «πανταχού παρών». Απλώς, κατά τον Γκέντελ, δεν είναι έτσι. Εφόσον ο χρόνος απουσιάζει από ένα δυνατό σύμπαν, θα πρέπει να συμπεράνουμε πως είναι ανύπαρκτος και στο δικό μας κόσμο! «[Ε]φόσον αυτός ο δυνατός κόσμος διέπεται από τους ίδιους φυσικούς νόμους που ισχύουν και στον πραγματικό κόσμο –και αφού η μόνη διαφορά έγκειται στη μεγάλης κλίμακας κατανομή της ύλης και της κίνησης-, ο χρόνος δεν μπορεί να είναι ανύπαρκτος στον πρώτο και να υπάρχει στο δεύτερο. Όποιος δε δέχεται αυτό το συλλογισμό, έλεγε ο Γκέντελ, είναι σα να λέει ότι «το αν υπάρχει ή όχι αντικειμενική παρέλευση του χρόνου…, εξαρτάται από τη συγκεκριμένη διάταξη της ύλης και της κίνησης σε αυτόν τον κόσμο»… [Μ]πορεί να αποδειχτεί πως ο χρόνος δεν μπορεί να υπάρξει στο σύμπαν Γκέντελ. Άρα, δεν μπορεί να υπάρχει ούτε στο δικό μας. Με την ολοκλήρωση του τελικού βήματος, πέφτει και η αυλαία: ο χρόνος πραγματικά εξαφανίζεται» (σελ. 188). Η δομή του επιχειρήματος, που με απελπιστικά συνοπτικό τρόπο εκτέθηκε, είναι πολύ λεπτή, συνεκτική, αλλά και φιλοσοφικά ενημερωμένη. Το κείμενο ξεκίνησε με αναφορά στο Χάιντεγκερ. Όχι τυχαία: ο Γκέντελ, αλλά και ο Αϊνστάιν, μοιράζονται μαζί του την υποτίμηση της επιστημολογίας μπροστά στην οντολογία και μαζί την απόρριψη του θετικισμού –εδώ, μάλιστα, ο Yourgrau παραπέμπει και στον Λένιν του Υλισμού και Εμπειριοκριτικισμού. Υπάρχει, όμως, και μια επιπλέον σχέση. Παραθέτω, χωρίς περαιτέρω σχολιασμό, σχεδόν σα γρίφο προς επίλυση μέσω της ανάγνωσης του βιβλίου: «[Μ]πορούμε να δεχτούμε έναν κόσμο όπου υπάρχει χρόνος ή έναν κόσμο όπου υπάρχει ύπαρξη –όχι όμως και τα δύο. Ο Γκέντελ έκανε τη μόνη δυνατή επιλογή: διάλεξε έναν κόσμο χωρίς χρόνο» (σελ. 190).
Ένας κόσμος δίχως χρόνο, λοιπόν, ο κόσμος μας. Διευκολυνόμαστε, άρα, να δούμε τη ζωή μας sub specie aeternitatis («από την σκοπιά της αιωνιότητας»), όπως μας καλεί ο καλός Σπινόζα, μια και, επιπλέον, ο θάνατος δεν μας είναι γνωστός παρά μόνο «εξ ασαφούς εμπειρίας». Δεν είναι τυχαίο πως τελειώνω με αναφορά στο Σπινόζα –ήταν ο αγαπημένος φιλόσοφος του Αϊνστάιν και είναι βάσιμη η υποψία πως η Γενική Θεωρία της Σχετικότητας χρωστάει φιλοσοφικά πολλά στην «Ηθική» του Σπινόζα. Και αυτό δεν είναι μια άλλη ιστορία ….
Χ. Λάσκος
Αναδημοσίευση απο τις “Αναγνώσεις” της εφημερίδας “Αυγή” , 2-11-2008
