Τράπεζα θεμάτων για τα μαθηματικά της Α Λυκείου:
Αρχείο για την κατηγορία 'ΛΥΚΕΙΟ'
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ
Δημοσιευμένο στην κατηγορία ΛΥΚΕΙΟ στις 13 Ιούν 2014
Ο πύργος του Ανόι
Δημοσιευμένο στην κατηγορία ΑΛΓΕΒΡΑ, Γ΄ ΓΥΜΝΑΣΙΟΥ, ΛΥΚΕΙΟ, ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΔΙΑΣΚΕΔΑΣΗ στις 17 Ιαν 2014
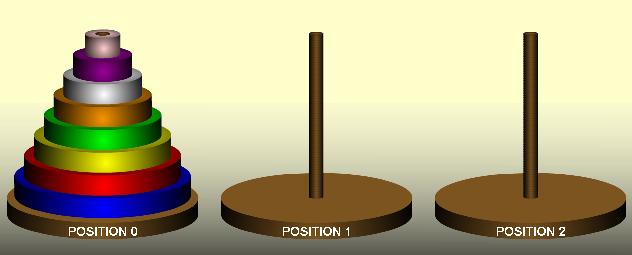
Ο Πύργος του Ανόι
ένα ακόμη ενδιαφέρον παιχνίδι. Ο παίκτης πρέπει να μεταφέρει τους δίσκους του πύργου έναν-έναν σε μία άλλη στήλη, έχοντας βοηθητική μία τρίτη στήλη. Ένας σημαντικός κανόνας του παιχνιδιού είναι ότι δεν μπορεί να τοποθετηθεί ούτε μία φορά ένας δίσκος πάνω σε έναν μικρότερο του.
Πατήστε στην εικόνα που ακολουθεί για να παίξετε. Ξεκινάτε το παιχνίδι με 3 δίσκους στον πρώτο πύργο που πρέπει να τους μεταφέρετε στον τελευταίο (τρίτο πύργο). Μετά ανεβάζετε τη δυσκολία αυξάνοντας τον αριθμό τους.
Μία ενδιαφέρουσα ιστορική παρένθεση σχετικά με τον Πύργο του Ανόι λέει ο παρακάτω θρύλος με τίτλο:
« Πύργος του Βράχμα »
«Όταν ο Βράχμα δημιούργησε τον κόσμο, έστησε σε ένα ναό στην πόλη Μπενάρες, 64 δακτυλίδια άνισου μεγέθους όλα περασμένα σένα μπαστούνι έτσι ώστε αν κρατήσουμε το μπαστούνι κατακόρυφα να σχηματίζουν τον γνωστό μας πύργο.
Oι ιερείς του ναού έπρεπε να δουλεύουν μέρα νύχτα, χωρίς σταμάτημα, για να μεταφέρουν τα δακτυλίδια σένα άλλο μπαστούνι, χρησιμοποιώντας ένα τρίτο σαν βοηθητικό, έτσι ώστε να μην τοποθετήσουν μεγαλύτερο δακτυλίδι πάνω από μικρότερο και μετακινώντας ένα μόνο δακτυλίδι σε κάθε κίνηση.
Ο θρύλος λέει πως πριν προλάβουν οι ιερείς να μεταφέρουν όλα τα δακτυλίδια στο άλλο μπαστούνι, ο ναός θα καταρρεύσει μέσα στην σκόνη και ο κόσμος θα χαθεί μέσα σε τρομακτικό κρότο βροντής».
Είχε άραγε ο Βράχμα δίκιο;
Δείτε την απάντηση:
http://3gym-serron.ser.sch.gr/OLDSITE/Anoi.htm
Περισσότερες προκλήσεις με τον Πύργο του Ανόι εδώ:
http://www.cut-the-knot.org/recurrence/hanoi.shtml
Ενα έξυπνο παιχνίδι για μικρούς και μεγάλους
Δημοσιευμένο στην κατηγορία ΑΛΓΕΒΡΑ, Β΄ΓΥΜΝΑΣΙΟΥ, ΛΥΚΕΙΟ, ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΔΙΑΣΚΕΔΑΣΗ στις 13 Ιαν 2014
Θέλετε να παίξουμε ένα έξυπνο παιχνίδι; Παίζοντας το θα ανακαλύψετε πόσο έξυπνος είναι ο υπολογιστής σας, ότι μπορεί να καταλαβαίνει τι σκέφτεστε και ότι υπάρχουν μαγικά κόλπα…
Ας δούμε όμως πώς παίζεται.
και ακολουθείτε τις παρακάτω οδηγίες πατώντας ![]() :
:
1)Βλέπετε έναν πίνακα με αριθμούς. Πρέπει να διαλέξετε έναν από αυτούς π.χ. ![]() . Μην τον πείτε σε κανέναν, μόνο σκεφτείτε τον με το μυαλό σας.
. Μην τον πείτε σε κανέναν, μόνο σκεφτείτε τον με το μυαλό σας.
2)Παρατηρήστε το χρώμα του αριθμού σας και επιλέξτε το ίδιο χρώμα στη γραμμή με τα χρώματα, που ακολουθεί π.χ. ![]() . Απομνημονεύστε τον αριθμό σας.
. Απομνημονεύστε τον αριθμό σας.
3)Τώρα πρέπει να διαλέξετε ένα από τα παρακάτω χρώματα.  Διαλέξτε αυτό που σας αρέσει.
Διαλέξτε αυτό που σας αρέσει.
4)Μια σειρά από σπιτάκια περιέχουν αριθμούς, έξι διαφορετικούς αριθμούς το καθένα. Βρείτε σε ποιο σπιτάκι βρίσκεται ο αριθμός σας και επιλέξτε το  .
.
5)Λίγα μαγικά …. πατήστε πάνω σε μία μπάλα…. Προσέξτε μη μαρτυρήσετε τον αριθμό σας, μην τον πείτε πουθενά. Το μηχάνημα σας ….ίσως σας ακούει …… ίσως λαμβάνει τη σκέψη σας ……ίσως![]() .
.
6)Βλέπετε τρεις πόρτες  Πατήστε πάνω σε μία από αυτές. Μήπως είναι ο δικός σας αριθμός μέσα; Πώς έγινε αυτό;
Πατήστε πάνω σε μία από αυτές. Μήπως είναι ο δικός σας αριθμός μέσα; Πώς έγινε αυτό;
Ωραία περάσαμε, παίξαμε και ξαφνιαστήκαμε με τα … μαγικά. Μήπως όμως πίσω από όλα αυτά κρύβονται τα μαθηματικά; Μήπως μπορούμε να δώσουμε μια εξήγηση; Πώς λειτουργεί το παιχνίδι;
Εναλλακτικά μπορείτε να παίξετε ΕΔΩ
Ο καθένας μας μπορεί να φτιάξει ένα δικό του παιχνίδι και να παίξει με τους φίλους του, προβληματίζοντας τους αρκετά με το πώς βρίσκουμε τον αριθμό που έχουν επιλέξει …
Μαθημαγικά
Δημοσιευμένο στην κατηγορία ΑΛΓΕΒΡΑ, Γ΄ ΓΥΜΝΑΣΙΟΥ, ΛΥΚΕΙΟ στις 16 Φεβ 2013
Τα τελευταία 30 χρόνια, ο Arthur Benjamin συνδυάζει επί σκηνής τα δύο του μεγάλα πάθη, τα μαθηματικά και τη μαγεία. Χιλιάδες άνθρωποι από όλο τον κόσμο έχουν παρακολουθήσει τις μαθημαγικές παραστάσεις του.
Tη διοργάνωση επιμελήθηκε ο Νικόλαος Πρωτονοτάριος στον όμορφο χώρο των Κάτω Πετραλώνων “ The Hub Event”.
http://www.blod.gr/lectures/Pages/viewlecture.aspx?LectureID=716
ΤΡΙΓΩΝΟ ΑΒΓ: Κατασκευή – Εμβαδό – Ισοδύναμα τρίγωνα
Δημοσιευμένο στην κατηγορία Β΄ΓΥΜΝΑΣΙΟΥ, ΓΕΩΜΕΤΡΙΑ, ΛΥΚΕΙΟ στις 27 Νοέ 2012
1) ΚΑΤΑΣΚΕΥΗ ΤΡΙΓΩΝΟΥ ΑΒΓ
Δίνονται τρεις αριθμοί α, β, γ. Μπορούμε πάντα να κατασκευάζουμε τρίγωνο με πλευρές τα μήκη α, β, γ;
Ποια σχέση πρέπει να συνδέει τα α, β, γ ώστε να κατασκευάζεται τρίγωνο;
Εναλλακτικά το αρχείο ΕΔΩ
ααα
- Το παραπάνω τρίγωνο που βλέπετε έχει κατασκευαστεί με μήκη πλευρών 9.4εκ, 8.3εκ, 6.6εκ.
Μπορείτε να κατασκευάσετε τρίγωνο με μήκη πλευρών του 4εκ, 6εκ, 15εκ; Ναι ή όχι και γιατί;
ααα
2) ΥΨΗ ΤΡΙΓΩΝΟΥ ΑΒΓ
Πόσα ύψη έχει ένα τρίγωνο; Που τέμνονται; Από τι εξαρτάται η θέση του σημείου τομής τους;
Ασχοληθήτε με τη δραστηριότητα που προτείνεται.
(Πατήστε πάνω στην εικόνα τριγώνων)
Εναλλακτικά το αρχείο ΕΔΩ
ααα
3) ΤΥΠΟΣ ΕΜΒΑΔΟΥ ΤΡΙΓΩΝΟΥ ΑΒΓ
Να βρείτε τον τύπο εμβαδού τριγώνου, όταν είναι γνωστός ο τύπος εμβαδού παραλληλογράμμου.
(Πατήστε πάνω στην εικόνα που ακολουθεί)

Εναλλακτικά το αρχείο ΕΔΩ
ααα
- Να αποδείξετε ότι ο τύπος του εμβαδού τριγώνου ΑΒΓ είναι:
(ΑΒΓ) = (α .υα)/2= (β . υβ)/2 =(γ . υγ) /2
οπου α, β, γ είναι οι πλευρές του τριγώνου και υα, υβ, υγ είναι τα αντίστοιχα ύψη.
ααα
4) ΙΣΟΔΥΝΑΜΑ ΤΡΙΓΩΝΑ
Να βρείτε τη σχέση των εμβαδών τριγώνων με ίδια/ίση βάση και ίδιο/ίσο, το αντίστοιχο ύψος.
(Πατήστε πάνω στην εικόνα που ακολουθεί)

Εναλλακτικά το αρχείο ΕΔΩ
ααα
- Τα τρίγωνα του παρακάτω σχήματος είναι ισοδύναμα; Γιατί;
Δευτερεύοντα στοιχεία τριγώνου
Δημοσιευμένο στην κατηγορία Α΄ ΓΥΜΝΑΣΙΟΥ, ΓΕΩΜΕΤΡΙΑ Α΄, ΛΥΚΕΙΟ στις 12 Οκτ 2012
Μαθαίνουμε από τη Α΄γυμνασίου τη κατασκευή μεσοκαθέτου τμήματος και τη διχοτόμου γωνίας. Στη συνέχεια χρησιμοποιούμε τις κατασκευές αυτές για τη κατασκευή των τριών μεσοκαθέτων, διαμέσων, υψών και διχοτόμων τριγώνου.
Ας μελετήσουμε όμως τις ιδιότητες τους λιγο περισσότερο πατώντας πάνω στην εικόνα που ακολουθεί:
Το τετράγωνο του Sierpinski
Δημοσιευμένο στην κατηγορία ΛΥΚΕΙΟ, ΤΕΧΝΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ στις 5 Φεβ 2012
Το τετράγωνο του Sierpinski – Μοτίβα
Εμφανίζουμε κάθε μία λίστα τετραγώνων χωριστά και μελετάμε τον τρόπο δημιουργίας του σχήματος. Μελετάμε το μήκος της πλευράς των τετραγώνων και τον αριθμό τους, τη περίμετρο και το εμβαδό τους.
Εμφανίζουμε τη μία λίστα κατόπιν της άλλης και περιγράφουμε το σχήμα που προκύπτει. Επαναλαμβάνουμε τη προηγούμενη μελέτη για το τελικό σχήμα.
Αν υποθέσουμε ότι επαναλαμβάνουμε την ίδια διαδικασία πολλές πολλές φορές έχουμε το τετράγωνο του Sierpinski.
Πατήστε την εικόνα παραπάνω για να πειραματιστείτε, ενναλακτικά εδώ :Sierpinski_square
Mπορούμε να υπολογίσουμε τη περίμετρο και το εμβαδό της επιφάνειας μεταξύ του σχήματος όλων των τετραγώνων (ροζ χρώματος) και του αρχικού τετραγώνου;
Τι παρατηρούμε;
Το τρίγωνο του Sierpinski
Δημοσιευμένο στην κατηγορία Γ΄ ΓΥΜΝΑΣΙΟΥ, ΓΕΩΜΕΤΡΙΑ, ΛΥΚΕΙΟ, ΤΕΧΝΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ στις 31 Ιαν 2012
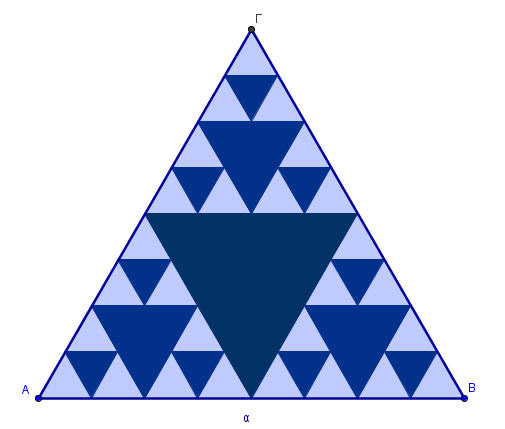
Υποθέτουμε ότι έχουμε ένα ισόπλευρο τρίγωνο ΑΒΓ.
Βρίσκουμε τα μέσα των πλευρών του και σχηματίζουμε τα τέσσερα ισόπλευρα τρίγωνα από τα οποία αφαιρούμε το μεσαίο.Εχουμε το βασικό μοτίβο, σχήμα 1.
Συνεχίζουμε την ίδια διαδικασία στα τρίγωνα που εναπομένουν.
Αν επαναλάβουμε τη διαδικασία πάρα πολλές φορές το τρίγωνο που δημιουργείται ονομάζεται τρίγωνο του Sierpinski.
Είναι ενδιαφέρον να υπολογίσουμε τη περίμετρο και το εμβαδό αυτού του τριγώνου.Για ν επαναλήψεις, όπου ν μεγάλος αριθμός, το εμβαδό του τείνει να γίνει 0 τ.μ, ενώ η περίμετρος του τείνει στο άπειρο. Ας δοκιμάσουμε πατώντας πάνω στην εικόνα που ακολουθεί.
Ας δούμε ένα άλλο τρίγωνο, το τρίγωνο Pascal .
Πιστεύετε ότι έχει κάποια σχέση με το τρίγωνο του Sierpinski ;
Οι αριθμοί Fibonacci 1,1, 2, 3, 5, 8, 13, 21,…
προκύπτουν ως εξής: 1, 1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, ….
Πιστεύετε ότι έχουν σχέση με το τρίγωνο του Pascal;
ΒΙΒΛΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΤΗΣ Α΄ ΛΥΚΕΙΟΥ
Δημοσιευμένο στην κατηγορία Ιστοσελίδες, ΛΥΚΕΙΟ στις 20 Σεπ 2011
Τα σχολικά βιβλία μετατράπηκαν σε ψηφιακή μορφή και στη συνέχεια εμπλουτίστηκαν με μικροπειράματα.
Εδω θα βρείτε το βιβλίο της Αλγεβρας
http://digitalschool.minedu.gov.gr/modules/ebook/show.php/DSGL-A100/261/1899,6291/
και εδώ θα βρείτε το βιβλίο της Γεωμετρίας
http://digitalschool.minedu.gov.gr/modules/ebook/show.php/DSGL-A101/216/1551,4988/
Μαθηματικό παράδοξο
Δημοσιευμένο στην κατηγορία Β΄ΓΥΜΝΑΣΙΟΥ, ΓΕΩΜΕΤΡΙΑ, ΛΥΚΕΙΟ στις 10 Απρ 2011
Παράδοξο !!!
Οταν η ρόδα ποδηλάτου, κάνει μια πλήρη περιστροφή τα φωτάκια κόκκινο και μπλε θα έχουν κάνει το καθενα, επίσης μια στροφή.
Τοτε συμπεραίνουμε ότι το μήκος των κύκλων των φώτων,
κόκκινου και του μπλε θα είναι ίσοι.
ΕΙΝΑΙ ΟΜΩΣ ΙΣΟΙ ΟΙ ΔΥΟ ΚΥΚΛΟΙ ???
Πατείστε πάνω στο σχήμα που ακολουθεί για να το διερευνήσετε
Για ανάλυση οθόνης 1024×768 κατεβάστε το αρχείο από εδώ