popiardv's blog

Οι μαθητές μέχρι τα μέσα της Β΄Γυμνασίου γνωρίζουν και εργάζονται στα μαθηματικά τους με αριθμούς  που τους διαχωρίζουν σε φυσικούς, ακέραιους και ρητούς ή κλασματικούς. Μπορούν να τους απεικονίζουν σε μια αριθμογραμμή και έχουν τη βεβαιότητα ότι κάθε αριθμός ακέραιος ή δεκαδικός έχει μία μοναδική θέση στην αριθμογραμμή και αντίστροφα κάθε σημείο της αριθμογραμμής απέχει από το 0 απόσταση ίση με έναν αριθμό φυσικό ή δεκαδικό / κλασματικό. Εχουν μία μεγάλη σιγουριά ότι όλοι αυτοί οι αριθμοί (ρητοί) καλύπτουν πλήρως την αριθμογραμμή.

Ας δούμε όμως τον προβληματισμό τους στο παρακάτω πρόβλημα, ένα πρόβλημα που φαίνεται από τον διάλογο “Μένων” του Πλάτωνα, ότι απασχολούσε τους “φιλόσοφους”  από την αρχαιότητα.

Το

Το πρόβλημα:αα

Να κατασκευαστεί ένα τετράγωνο που έχει διπλάσιο εμβαδόν από ένα άλλο δοσμένο.

Στον διάλογο αυτό ο Σωκράτης καταφέρνει με τις μεθόδους του, την μαιευτική και επαγωγική σκέψη, ο δούλος του Μένωνα να λύσει το πρόβλημα.

Ο διπλασιασμός της πλευράς του αρχικού τετραγώνου οδηγεί σε τετραπλασιασμό του εμβαδού του.  Ποιο μήκος άρα γε οδηγεί στο διπλασιασμό του εμβαδού του τετραγώνου; Αν ενώσουμε τις διαγώνιες των τετραγώνων αυτών παίρνουμε ένα τετράγωνο διπλάσιο του αρχικού, όπως εύκολα διαπιστώνουμε από το παραπάνω σχήμα.

Η πλευρά του τετραγώνου και η διαγώνιος του είναι μεγέθη ασύμμετρα.

Αν υποθέσουμε ότι το εμβαδόν του αρχικού τετραγώνου είναι 1 cm^2 πόσο μήκος έχει η πλευρά του τετραγώνου με διπλάσιο εμβαδόν; Οι μαθητές εφαρμόζουν το Πυθαγόρειο Θεώρημα και απαντούν ότι η νέα πλευρά είναι η λύση της εξίσωσης χ^2=2. Ποιου αριθμού το τετράγωνο ισούται με 2; Με δοκιμές βρίσκουν  χ=1,414, με προσέγγιση χιλιοστού και  με έναν υπολογιστή:

Ο αριθμός αυτός είναι δεκαδικός, απειροψήφιος, μη περιοδικός και τον ονομάζουμε ΑΡΡΗΤΟ. Οι άρρητοι είναι όλοι οι αριθμοί που δεν είναι ρητοί, δεν μπορεί δηλαδή να εκφραστούν ως πηλίκο δύο ακεραίων.

Απεικονίζουμε τον άρρητο αυτό στην αριθμογραμμή καθώς αλλά και οποιονδήποτε άλλον αφού τον κατασκευάσουμε γεωμετρικά.

Οι άρρητοι με τους ρητούς αποτελούν το σύνολο των πραγματικών αριθμών και ισχύει ότι “κάθε πραγματικός αριθμός  έχει μία μοναδική θέση στην αριθμογραμμή και αντίστροφα κάθε σημείο της αριθμογραμμής απέχει από το 0 απόσταση ίση με την απόλυτη τιμή κάποιου πραγματικού αριθμού. Ολοι  οι πραγματικοί αριθμοί καλύπτουν πλήρως την αριθμογραμμή.

Μερικές από τις δημιουργίες μαθητών για την κατασκευή του Πυθαγόρειου σπιράλ: https://blogs.sch.gr/popiardv/archives/1610

ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ

Μερικές αποδείξεις για το Πυθαγόρειο Θεώρημα μπορεί να σας εντυπωσιάσουν. Ασχοληθείτε με κάθε μία από αυτές που ακολουθούν και προσπαθήστε να την εξηγήσετε. 

Απόδειξη 1:

Απόδειξη 2:

Απόδειξη 3: 

Ένα Πυθαγόρειο Δέντρο: 

Ένα Πυθαγόρειο παραμύθι:

Θέλετε να παίξουμε ένα έξυπνο παιχνίδι; Παίζοντας το θα ανακαλύψετε πόσο έξυπνος είναι ο υπολογιστής σας, ότι μπορεί να καταλαβαίνει τι σκέφτεστε και ότι υπάρχουν μαγικά κόλπα… 

Ας δούμε όμως πώς παίζεται.

Αρχικά πατάτε εδώ στο σπιτάκι 

και ακολουθείτε τις παρακάτω οδηγίες πατώντας :

1)Βλέπετε έναν πίνακα με αριθμούς. Πρέπει να διαλέξετε έναν από αυτούς π.χ. . Μην τον πείτε σε κανέναν, μόνο σκεφτείτε τον με το μυαλό σας.

2)Παρατηρήστε το χρώμα του αριθμού σας και επιλέξτε το ίδιο χρώμα στη γραμμή με τα χρώματα, που ακολουθεί π.χ. . Απομνημονεύστε τον αριθμό σας.

3)Τώρα πρέπει να διαλέξετε ένα από τα παρακάτω χρώματα.  Διαλέξτε αυτό που σας αρέσει.

4)Μια σειρά από σπιτάκια περιέχουν αριθμούς, έξι διαφορετικούς αριθμούς το καθένα. Βρείτε σε ποιο σπιτάκι βρίσκεται ο αριθμός σας και επιλέξτε το .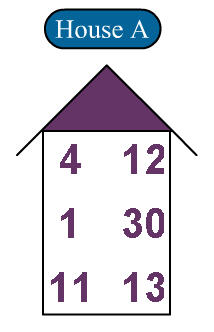

5)Λίγα μαγικά …. πατήστε πάνω σε μία μπάλα…. Προσέξτε μη μαρτυρήσετε τον αριθμό σας, μην τον πείτε πουθενά. Το μηχάνημα σας ….ίσως σας ακούει …… ίσως λαμβάνει τη σκέψη σας ……ίσως.

6)Βλέπετε τρεις πόρτες Πατήστε πάνω σε μία από αυτές. Μήπως είναι ο δικός σας αριθμός μέσα; Πώς έγινε αυτό;

Ωραία περάσαμε, παίξαμε και ξαφνιαστήκαμε με τα … μαγικά. Μήπως όμως πίσω από όλα αυτά κρύβονται τα μαθηματικά; Μήπως μπορούμε να δώσουμε μια εξήγηση; Πώς λειτουργεί το παιχνίδι;

Εναλλακτικά μπορείτε να παίξετε ΕΔΩ 

 Ο καθένας μας μπορεί να φτιάξει ένα δικό του παιχνίδι και να παίξει με τους φίλους του, προβληματίζοντας τους αρκετά με το πώς βρίσκουμε τον αριθμό που έχουν επιλέξει …

Ένας γρίφος για μικρούς και μεγάλους.

Τέσσερα διαφορετικά κομμάτια σχηματίζουν διάφορα σχέδια, όπως αυτό του σχήματος παρακάτω. Παίξε κι εσύ και σχημάτισε δικά σου σχέδια χρησιμοποιώντας κάθε φορά τα τέσσερα αυτά κομμάτια.

Προσπάθησε να κατασκευάσεις το κεφαλαίο γράμμα ΤΑΥ.  Μετά απάντησε στο ερώτημα: Ποιο είναι το εμβαδόν του  σχήματος που σχηματίζεται κάθε φορά από τα τέσσερα αυτά κομμάτια;

Κάνε κλικ πάνω στην εικόνα για να ανοίξεις το αρχείο (geogebra)

πηγή: http://www.mathematikum.de/

Μια ακόμη οπτική  “απόδειξη”  του πυθαγορείου θεωρήματος με το λογισμικό Geogebra

Δοκιμάστε: