Οι μαθητές μέχρι τα μέσα της Β΄Γυμνασίου γνωρίζουν και εργάζονται στα μαθηματικά τους με αριθμούς που τους διαχωρίζουν σε φυσικούς, ακέραιους και ρητούς ή κλασματικούς. Μπορούν να τους απεικονίζουν σε μια αριθμογραμμή και έχουν τη βεβαιότητα ότι κάθε αριθμός ακέραιος ή δεκαδικός έχει μία μοναδική θέση στην αριθμογραμμή και αντίστροφα κάθε σημείο της αριθμογραμμής απέχει από το 0 απόσταση ίση με έναν αριθμό φυσικό ή δεκαδικό / κλασματικό. Εχουν μία μεγάλη σιγουριά ότι όλοι αυτοί οι αριθμοί (ρητοί) καλύπτουν πλήρως την αριθμογραμμή.
Ας δούμε όμως τον προβληματισμό τους στο παρακάτω πρόβλημα, ένα πρόβλημα που φαίνεται από τον διάλογο “Μένων” του Πλάτωνα, ότι απασχολούσε τους “φιλόσοφους” από την αρχαιότητα.
Το

Το πρόβλημα:αα
Να κατασκευαστεί ένα τετράγωνο που έχει διπλάσιο εμβαδόν από ένα άλλο δοσμένο.
Στον διάλογο αυτό ο Σωκράτης καταφέρνει με τις μεθόδους του, την μαιευτική και επαγωγική σκέψη, ο δούλος του Μένωνα να λύσει το πρόβλημα.
Ο διπλασιασμός της πλευράς του αρχικού τετραγώνου οδηγεί σε τετραπλασιασμό του εμβαδού του. Ποιο μήκος άρα γε οδηγεί στο διπλασιασμό του εμβαδού του τετραγώνου; Αν ενώσουμε τις διαγώνιες των τετραγώνων αυτών παίρνουμε ένα τετράγωνο διπλάσιο του αρχικού, όπως εύκολα διαπιστώνουμε από το παραπάνω σχήμα.
Η πλευρά του τετραγώνου και η διαγώνιος του είναι μεγέθη ασύμμετρα.
Αν υποθέσουμε ότι το εμβαδόν του αρχικού τετραγώνου είναι 1 cm^2 πόσο μήκος έχει η πλευρά του τετραγώνου με διπλάσιο εμβαδόν; Οι μαθητές εφαρμόζουν το Πυθαγόρειο Θεώρημα και απαντούν ότι η νέα πλευρά είναι η λύση της εξίσωσης χ^2=2. Ποιου αριθμού το τετράγωνο ισούται με 2; Με δοκιμές βρίσκουν χ=1,414, με προσέγγιση χιλιοστού και με έναν υπολογιστή:
Ο αριθμός αυτός είναι δεκαδικός, απειροψήφιος, μη περιοδικός και τον ονομάζουμε ΑΡΡΗΤΟ. Οι άρρητοι είναι όλοι οι αριθμοί που δεν είναι ρητοί, δεν μπορεί δηλαδή να εκφραστούν ως πηλίκο δύο ακεραίων.
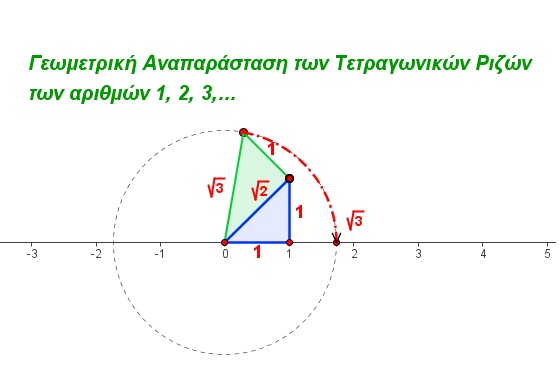
Απεικονίζουμε τον άρρητο αυτό στην αριθμογραμμή καθώς αλλά και οποιονδήποτε άλλον αφού τον κατασκευάσουμε γεωμετρικά.
Οι άρρητοι με τους ρητούς αποτελούν το σύνολο των πραγματικών αριθμών και ισχύει ότι “κάθε πραγματικός αριθμός έχει μία μοναδική θέση στην αριθμογραμμή και αντίστροφα κάθε σημείο της αριθμογραμμής απέχει από το 0 απόσταση ίση με την απόλυτη τιμή κάποιου πραγματικού αριθμού. Ολοι οι πραγματικοί αριθμοί καλύπτουν πλήρως την αριθμογραμμή.
Μερικές από τις δημιουργίες μαθητών για την κατασκευή του Πυθαγόρειου σπιράλ: https://blogs.sch.gr/popiardv/archives/1610
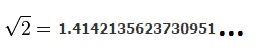
Αφήστε μια απάντηση
Για να σχολιάσετε πρέπει να συνδεθείτε.