ΜΕΡΟΣ Α΄
Τ Ρ Ι Γ Ω Ν Ο Π Α Σ Κ Α Λ
Γνωριμία και Κατασκευή
Παρατηρήστε το παραπάνω σχήμα, το οποίο σχηματίζεται από τετράγωνα τοποθετημένα το ένα πάνω στο άλλο σε τριγωνική διάταξη.
Παρατηρήστε την αρίθμηση των τετραγώνων από πάνω προς τα κάτω. Συμπληρώστε 30 σειρές τετραγώνων (η 30η σειρά θα αποτελείται από 30 τετράγωνα) και αριθμήστε κατάλληλα.
Περιγράψτε όλα τα μοτίβα που βρήκατε για την κατασκευή του τριγώνου Πασκάλ.
–> Στο σχήμα σας τα τετράγωνα να έχουν πλευρά 1 cm
–>Βοηθητικά στην επόμενη, 6η γραμμή υπάρχουν 6 τετράγωνα με τους αριθμούς: 1, 5, 10, 10, 5, 1 .
ΜΕΡΟΣ Β΄
Έλεγχος της κατασκευής: Πριν συνεχίσουμε για το Β΄μέρος της εργασίας μας ας ελέγξουμε την κατασκευή μας σε όσο αφορά τους αριθμούς που γράψαμε στα κουτάκια κάθε γραμμής από εδώ
Επιδιορθώνουμε την κατασκευή μας και συνεχίζουμε με τα παρακάτω ερωτήματα:
Ιδιότητες του τριγώνου Πασκάλ
1) Παρατηρήστε το είδος του “τριγώνου” που σχηματίσατε. Ποιοι αριθμοί οριοθετούν δύο από τις πλευρές του;
2) Το σχήμα σας έχει άξονα συμμετρίας; ποιον – ποιους;
3)Πώς έχουν προκύψει οι αριθμοί σε κάθε σειρά του; Βλέπετε κάποιο είδος “συμμετρίας” ;
4)Παρατηρήστε τους αριθμούς που σχηματίζουν την 1η διαγώνιο του. Ποιοι είναι;
Το άθροισμα 1+2+3+4=10 Ποιος αριθμός βρίσκεται κάτω δεξιά από το 4; Τι παρατηρείτε; Ισχύει το ίδιο για το άθροισμα 1+2+3+4+5; για άλλα αθροίσματα; Σχετικά με το άθροισμα των ν πρώτων φυσικών αριθμών ισχύει ο τύπος Σν = ν (ν+1) /2 (περισσότερα εδώ)
5)Παρατηρήστε τους αριθμούς που σχηματίζουν τη δεύτερη διαγώνιο του. Αυτοί λέγονται τριγωνικοί αριθμοί γιατί μπορούν να παρασταθούν με ψηφίδες, σχηματίζοντας τρίγωνο. (Για περισσότερες πληροφορίες εδώ)
6)Παρατηρήστε τους αριθμούς που σχηματίζουν την τρίτη διαγώνιο του. Αυτοί λέγονται τετραεδρικοί αριθμοί, γιατί μπορούν να παρασταθούν στο χώρο των τριών διαστάσεων με ψηφίδες, σχηματίζοντας τετράεδρο.
7)Βρείτε το άθροισμα των αριθμών κάθε γραμμής του τριγώνου Πασκάλ. Τι παρατηρείτε;
Ποια σχέση έχουν τα αθροίσματα αυτά με τον αριθμό 2;
8)Υπολογίζουμε το 11^3 και βρίσκουμε ότι
11^3 = 1331 = 1*10^3 + 3* 10 ^2 + 3*10 +1
Μήπως βλέπετε τους συντελεστές 1, 3, 3, 1 σε κάποια γραμμή του τριγώνου Πασκάλ;
Εξετάστε το ίδιο για άλλες δυνάμεις του 11. Τι παρατηρείτε;
9)Ας δούμε τα αναπτύγματα των πολυωνύμων
(α+β)^0 =1
(α+β)^1 =α+β =1*α + 1*β
(α+β)^2= α^2+ 2 *α*β +β^2 = 1 *α^2 + 2 *α *β +1 * β^2
(α+β)^3= α^3 + 3 *α^2 * β + 3 *α* β^2 + β^3 =
1 * α^3 + 3 * α ^2 * β + 3 *α* β^2 + 1* β^3
Έχουν σχέση οι παραπάνω συντελεστές των πολυωνύμων με αριθμούς μιας γραμμής του τριγώνου Πασκάλ;
Πρόσθετα (α+β)^3 = α^3 + 3 * α ^2 * β + 3 *α* β^2 + 1* β^3
Παρατηρήστε ότι ο συντελεστής του δεύτερου όρου προκύπτει από το γινόμενο του συντελεστή του προηγούμενου όρου επί τον εκθέτη του α,
δηλαδή 1 *3 =3
Ο συντελεστής του τρίτου όρου προκύπτει από το γινόμενο του συντελεστή του προηγούμενου όρου επί τον εκθέτη του α δια 2 ( 2ος όρος),
δηλαδή 3 *2 /2 =3
Ο συντελεστής του τέταρτου όρου προκύπτει από το γινόμενο του συντελεστή του προηγούμενου όρου επί τον εκθέτη του α δια 3 (3ος όρος) ,
δηλαδή 3*1/3 =1
Θα μπορούσαμε να βρούμε το ανάπτυγμα (α+β)^10 =; χωρίς απαραίτητα να έχουμε τους αριθμούς στο τρίγωνο Πασκάλ;
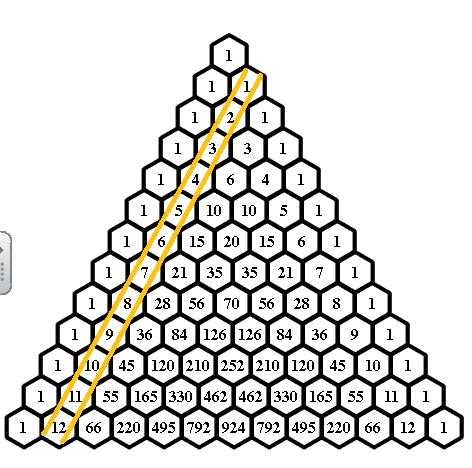
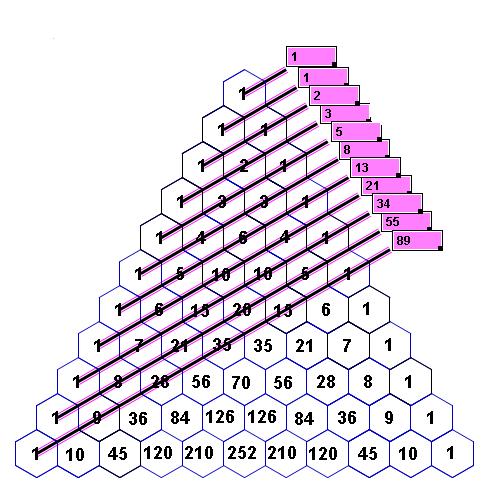
10) Βρείτε το άθροισμα των αριθμών σε κάθε διαγώνιο (Δεξιά ή αριστερά) και βρείτε τη σχέση τους με τους αριθμούς Fibonacci
Για περισσότερη βοήθεια στα τελευταία ερωτήματα εδώ
ααα
ααα
ΜΕΡΟΣ Γ΄
1) Καθένας από την ομάδα να χρωματίσει ένα μόνο από τα παρακάτω:
Με κίτρινο χρώμα τους αριθμούς του τριγώνου Πασκάλ που είναι πολλαπλάσιοι του 2 (άρτιοι αριθμοί)
Με πράσινο χρώμα τους αριθμούς του τριγώνου, που είναι πολ/σιοι του 3
Με μπλε χρώμα τους αριθμούς του τριγώνου, που είναι πολ/σιοι του 4
Με κόκκινο χρώμα τους αριθμούς του τριγώνου, που είναι πολ/σιοι του 5.
Τι παρατηρείτε; (ως ομάδα)
2)Ας κάνουμε την παρακάτω γεωμετρική κατασκευή:
Παίρνουμε ένα τρίγωνο στο μέγεθος του τριγώνου Πασκάλ (μέγεθος σύμφωνα με την αρχική κατασκευή) και βρίσκουμε τα μέσα των πλευρών του.
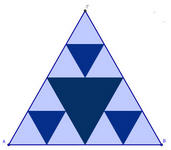
Ενώνουμε τα μέσα των πλευρών του και μετά επαναλαμβάνουμε το ίδιο στα τρίγωνα που σχηματίζονται, αφού εξαιρέσουμε το εσωτερικό τρίγωνο (Σκουρο χρώμα).
Συνεχίζουμε μερικές φορές ακόμη (5-6) με τον ίδιο τρόπο. Το τρίγωνο που φτιάξατε λέγεται τρίγωνο Σιερπίνσκι
Τι παρατηρείτε;
Ποιά σχέση μπορεί να έχει το τρίγωνο Πασκάλ με το τρίγωνο Σιερπίνσκι;
3)Τα Χριστούγεννα φτιάξαμε μικρά τρίεδρα.
Μπορούμε να τα τακτοποιήσουμε ώστε να έχουμε ένα τρίγωνο Σιερπίσνκι στο χώρο;
(η κατασκευή θα γίνει στο σχολείο από όλες τις ομάδες)
ΜΕΡΟΣ Δ΄
συνεχίζεται …..



Αφήστε μια απάντηση
Για να σχολιάσετε πρέπει να συνδεθείτε.