
Διδασκαλίες, Α’ Λυκείου – Γ’ Λυκείου, Η μέθοδος Monte Carlo
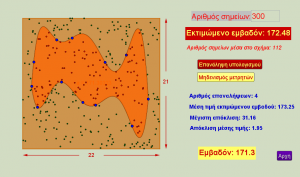
Ας υποθέσουμε ότι θα επιθυμούσαμε να υπολογίσουμε το εμβαδόν μιας επίπεδης μορφής για την οποία δεν υπάρχει κανένας τύπος που να την υπολογίζει επακριβώς. Υπάρχουν αρκετές μέθοδοι για να μπορέσουμε να το εκτιμήσουμε, όμως μια από τις πιο διασκεδαστικές είναι η ονομαζόμενη μέθοδος Monte Carlo που βασίζεται στις εαναλαμβανόμενες τυχαίες δειγματοληψίες. Η ιδέα είναι απλή: αρκεί να περιγράψουμε τη συγκεκριμένη μορφή με ένα ορθογώνιο του οποίου το εμβαδόν υπολογίζεται εύκολα, και στη συνέχεια να δημιουργήσουμε έναν αριθμό τυχαίων σημείων μέσα στο ορθογώνιο (π.χ. κρεμώντας το όλο σχήμα στον τοίχο και ρίχνοντας πάνω του βελάκια χωρίς να σημαδεύουμε)… Τότε αν δημιουργήσαμε 100 τέτοια σημεία μέσα στο ορθογώνιο, και από αυτά τα 60 κατέληξαν να είναι μέσα στην «περίεργη» μορφή, τότε το εκτιμώμενο εμβαδόν θα αντιστοιχεί στο 60% του εμβαδού του ορθογωνίου. Η συγκεκριμένη εφαρμογή αναπαριστά αυτή τη μέθοδο εκτίμησης εμβαδού, αλλά επιπλέον δείχνει και μια εφαρμογή της συγκεκριμένης μεθόδου στον υπολογισμό του π.
Θα μπορούσε να διδαχθεί στο μάθημα των πιθανοτήτων τόσο στην Α’, όσο και στα Μαθηματικά Γενικής Παιδείας στη Γ’ Λυκείου.
Για να μεταφορτώσετε το αρχείο κάνετε κλικ επάνω στην εικόνα.
06/10/2013 στις 6:48 πμ
Συγχαρητήρια για τη προσπάθειά σας. Είναι σε όλους μας χρήσιμη.