popiardv's blog

Ταιριάξτε το είδος της γωνίας ή των γωνιών στο αριστερό πλαίσιο με τον ορισμό του/της στο δεξί πλαίσιο.

Έχετε στη διάθεσή σας 5 λεπτά! Κάθε προσπάθεια βαθμολογείται θετικά (σωστό) ή αρνητικά (λάθος).

Ετοιμοι; πάμε:

Δημιουργός  : Κουλέτση Ειρήνη, ΠΕ03

ΚΑΛΗ ΕΠΙΤΥΧΙΑ!!!

Ας εξετάσουμε την ύπαρξη αξόνων και κέντρων συμμετρίας στο παραλληλόγραμμο, το ορθογώνιο, τον  ρόμβο και το τετράγωνο.

Μια προσομοίωση των παραπάνω σχημάτων στο λογισμικό Geogebra μας δίνει τη δυνατότητα να διπλώσουμε το σχήμα ή να το περιστρέψουμε για να βρούμε άξονες ή κέντρο συμμετρίας .

Θυμόμαστε ότι ένα σχήμα έχει άξονα συμμετρίας την ευθεία χχ΄όταν το διπλώσουμε, τσακίσουμε πάνω σε αυτή την ευθεία και παρατηρήσουμε να συμπίπτουν τα δύο μέρη του.

Θυμόμαστε ότι ένα σχήμα έχει κέντρο συμμετρίας Ο όταν το περιστρέψουμε 180 μοίρες γύρω από το Ο  και ταυτίζεται με το αρχικό του αποτύπωμα.

1η διδακτική ώρα:

Εκτυπώνουμε το αρχείο “4πλευρα”  και δίνουμε σε κάθε διάδα μαθητών ένα ή δύο διαφορετικά σχήματα να τα κόψουν  ακριβώς στο περίγραμμα τους  και το φύλλο εργασίας f_1 . Τα ονομάζουν πχ ΑΒΓΔ και σημειώνουν τα στοιχεία τους όπως κορυφές, πλευρές, γωνίες στο ΦΕ. Σχεδιάζουν και ονομάζουν τις διαγώνιες τους. Ζητάμε να παρατηρήσουν τι κοινό έχουν όλα αυτά τα διαφορετικά σχήματα. Το κοινό αυτό χαρακτηριστικό τους,  “τετράπλευρα” το βάζουν τίτλο στο φύλλο εργασίας τους. Στη συνέχεια ζητάμε από τους μαθητές να χρησιμοποιήσουν τα γεωμετρικά τους όργανα , για να μετρήσουν και να συμπεράνουν τυχόν σχέσεις μεταξύ των πλευρών , γωνιών, των διαγωνίων των τετραπλεύρων  και των μερών των διαγωνίων των σχημάτων. Συμπληρώνουν τη λίστα που ακολουθεί στο φύλλο εργασίας με τις ιδιότητες για το δικό τους σχήμα, όπως: “έχει τις απέναντι πλευρές ίσες” , “έχει τις απέναντι γωνίες ίσες” ,  “οι διαγώνιες διχοτομούνται” Κόβουν τις  επιλεγμένες προτάσεις και φτιάχνουν σε ένα κολάζ το σχήμα και τις προτάσεις με τις ιδιότητες του. Το τελευταίο μέρος μπορεί να δοθεί εργασία για το σπίτι.

2η διδακτική ώρα:

α)Η κάθε ομάδα παρουσιάζει την εργασία της στην τάξη.

Εναλλακτικά χρησιμοποιούμε τον διαδραστικό πίνακα εφ όσον υπάρχει. Εχουμε ετοιμάσει το αρχείο tetrapleyra έτσι ώστε σε κάθε σελίδα του να έχουμε όλες τις προτάσεις  και από ένα σχήμα. Ζητάμε να επιλέξουν για το σχήμα τους τις ανάλογες προτάσεις και ομαδοποιούμε το σχήμα με τις προτάσεις που το περιγράφουν. Σε όσα σχήματα χρειάζεται να επιβεβαιωθούν οι μετρήσεις τους, χρησιμοποιούν τα γεωμετρικά όργανα του διαδραστικού πίνακα .

β) Στη συνέχεια ζητάμε να βρουν ποια -ποιες από τις ιδιότητες είναι χαρακτηριστική-ές  για το δικό τους σχήμα και ποια κοινή με άλλα και προχωρούν σε ομαδοποίηση των σχημάτων. Αρχικά ίσως τα χωρίσουν σε δύο ομάδες τα τραπέζια (δύο μόνο πλευρές παράλληλες) και τα παραλληλόγραμμα (ανά δύο πλευρές παράλληλες). Με αυτό τον τρόπο διαχωρίζουν κάποιες από τις προτάσεις για τον ορισμό των σχημάτων και τις υπόλοιπες για τις ιδιότητές τους.

Αναμενόμενο είναι να  φτιάξουν έναν εννοιολογικό χάρτη όπως:

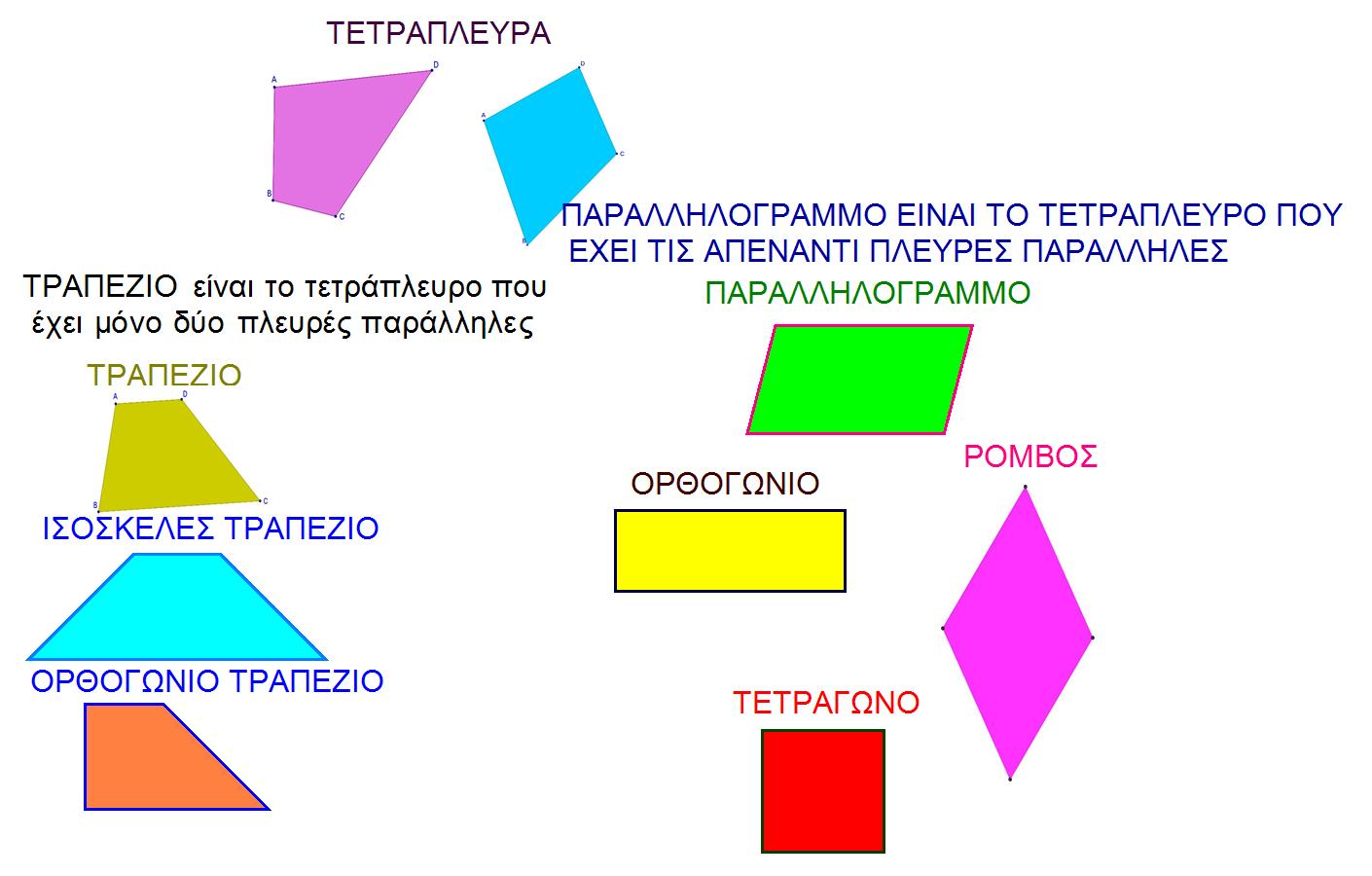
ή

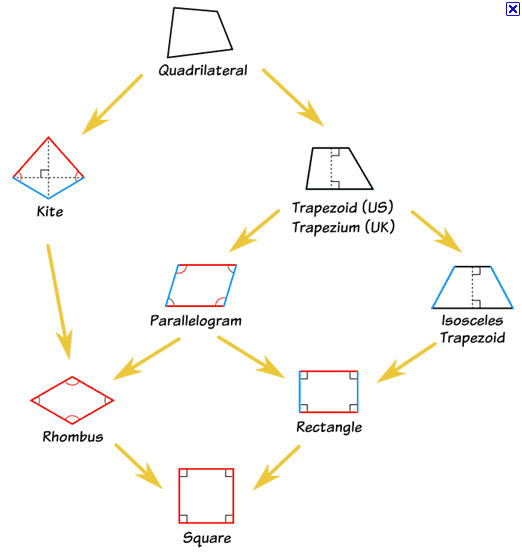
Παίζουμε με τα τετράπλευρα;

Μεταχηματισμοί τετραπλεύρων

Περισσότερες διερευνήσεις  στα τετράπλευρα