
Φεβ 13 2025
ημέρα φιλάθλου
Φεβ 09 2025
Ποιος μας έκλεψε την προσοχή μας;
Οι ειδικοί μιλούν για παγκόσμια «attention crisis». Όλοι και όλα τη διεκδικούν, το ζήτημα είναι ότι εμείς οι ίδιοι έχουμε απωλέσει τον έλεγχο του πιο ακριβού «νομίσματος» της εποχής. Δεν έχουμε επίγνωση ότι η θρυμματισμένη προσοχή μας έχει κόστος: σε φαιά ουσία, σε χρόνο, σε παραγωγικότητα (το στρες καλύτερα να μην το αναφέρουμε) Πηγή: Protagon.gr
Φεβ 06 2025
Τι είναι τελικά η εντροπία;
«Τίποτα στη ζωή δεν είναι σίγουρο εκτός από τον θάνατο, τους φόρους και τον δεύτερο νόμο της θερμοδυναμικής», έγραψε ο Seth Lloyd, ένας φυσικός στο Ινστιτούτο Τεχνολογίας της Μασαχουσέτης. Δεν μπορούμε να αποφύγουμε αυτή την μοίρα. Η αύξηση της εντροπίας είναι βαθιά συνυφασμένη με τις πιο βασικές εμπειρίες μας, εξηγώντας γιατί ο χρόνος ρέει προς το μέλλον και γιατί ο κόσμος φαίνεται ντετερμινιστικός και όχι κβαντομηχανικά αβέβαιος.
Η κινητήρια δύναμη της φωτιάς
Η έννοια της εντροπίας προέκυψε από μια προσπάθεια τελειοποίησης των μηχανών κατά τη διάρκεια της βιομηχανικής επανάστασης. Ένας 28χρονος Γάλλος στρατιωτικός μηχανικός ονόματι Sadi Carnot υπολόγισε την απόλυτη απόδοση μιας ατμοκίνητης μηχανής. Το 1824, δημοσίευσε ένα μικρό βιβλίο 118 σελίδων με τίτλο «Σκέψεις επί της κινητήριας δυνάμεως του πυρός» το οποίο επωλείτο στις όχθες του Σηκουάνα για 3 φράγκα και εξαντλήθηκε πολύ γρήγορα. Στο βιβλίο αυτό εισαγόταν έμμεσα για πρώτη φορά η έννοια της εντροπίας, μια ιδέα που θα ποσοτικοποιούσε τoν αδυσώπητo κατήφορο του σύμπαντος προς την φθορά.

Η επίδρασή του στην φυσική σε σχέση με την ποσότητα των γραπτών του, συγκρίνεται με εκείνη του Évariste Galois (1811-1832) στα μαθηματικά και του Arthur Rimbaud (1854-1891) στην ποίηση.
Ο Carnot πέθανε από χολέρα σε ηλικία 36 ετών, οκτώ χρόνια μετά την δημοσίευση του βιβλίου του, το οποίο αγνοήθηκε σε μεγάλο βαθμό από την επιστημονική κοινότητα. Ένα άρθρο που δημοσιεύτηκε το 1834 (δύο χρόνια μετά τον θάνατο του Carnot και δέκα χρόνια μετά τη δημοσίευση του βιβλίου του) από τον μηχανικό Émile Clapeyron κατάφερε τελικά να επιστήσει την προσοχή στο έργο του Carnot. Έτσι, μερικά χρόνια αργότερα χρησιμοποιήθηκε από τον Λόρδο Kelvin (o οποίος δυσκολεύθηκε πολύ να βρει αντίγραφο του βιβλίου του Carnot) και τον Rudolf Clausius για να ορίσουν τις έννοιες της απόλυτης θερμοκρασίας, της εντροπίας και να διατυπώσουν τον δεύτερο νόμο της Θερμοδυναμικής. Το 1890 δημοσιεύθηκε μια αγγλική μετάφραση του βιβλίου του Carnot από τον R.H. Thurston «Reflections on the Motive Power of Fire«.
Ο Carnot συνειδητοποίησε ότι η ατμομηχανή εκμεταλλεύεται την τάση της θερμότητας να ρέει από τα θερμά σώματα στα ψυχρά. Και σχεδίασε μια θερμική μηχανή με την μέγιστη απόδοση που μπορούσε να φανταστεί κανείς, θέτοντας ένα όριο στο κλάσμα της θερμότητας που μπορεί να μετατραπεί σε ωφέλιμο έργο, ένα αποτέλεσμα που σήμερα είναι γνωστό ως θεώρημα του Carnot. Η σπουδαιότερη δήλωσή του εμφανίζεται ως περιορισμός στην τελευταία σελίδα του βιβλίου: «Στην πράξη, δεν θα μπορέσουμε ποτέ να χρησιμοποιήσουμε όλη την κινητήρια δύναμη των καύσιμων υλικών». Κάποια ενέργεια θα διαχέεται πάντα μέσω τριβής, δονήσεων ή άλλης ανεπιθύμητης μορφής κίνησης. Η τελειότητα είναι ανέφικτη.
Διαβάζοντας το βιβλίο του Carnot μερικές δεκαετίες αργότερα, το 1865, ο Γερμανός φυσικός Rudolf Clausius εισήγαγε την έννοια της εντροπίας και στη συνέχεια διατύπωσε αυτό που έγινε γνωστό ως ο δεύτερος νόμος της θερμοδυναμικής: «Η εντροπία του σύμπαντος αυξάνεται».
Όμως, παρά την θεμελιώδη σημασία της, η εντροπία είναι ίσως η πιο διχαστική έννοια στη φυσική. Σύμφωνα με τον Lloyd: «Η εντροπία ήταν πάντα πρόβλημα. Η σύγχυση πηγάζει εν μέρει από τον τρόπο με τον οποίο ο όρος χρησιμοποιείται και διακινείται σε διάφορους τομείς- έχει παρόμοια, αλλά ξεχωριστή σημασία σε κάθε τομέα, από την φυσική έως τη θεωρία πληροφοριών, την οικολογία και την ψυχανάλυση. Αλλά για να κατανοήσουμε πραγματικά την έννοια της εντροπίας απαιτούνται κάποια βαθιά άβολα φιλοσοφικά άλματα.
Καθώς οι φυσικοί του περασμένου αιώνα εργάστηκαν για να ενώσουν φαινομενικά ανόμοια πεδία έριξαν στην έννοια της εντροπίας νέο φως, μετατόπισαν την συνήθη ερμηνεία της, από μέτρο της αταξίας σε μέτρο της άγνοιας. Η εντροπία δεν θεωρείται ως μια ιδιότητα εγγενής σε ένα σύστημα, αλλά ως μια ιδιότητα που σχετίζεται με έναν παρατηρητή που αλληλεπιδρά με το σύστημα. Αυτή η σύγχρονη άποψη φωτίζει τον βαθύ δεσμό μεταξύ της πληροφορίας και της ενέργειας, η οποία βοηθά τώρα να εγκαινιαστεί μια μίνι-βιομηχανική επανάσταση στις μικρότερες κλίμακες.
διαβάστε περισσότερα στο άρθρο του Zack Savitsky με τίτλο: «Τι είναι εντροπία; Ένα μέτρο για το πόσο λίγα γνωρίζουμε πραγματικά.» – https://www.quantamagazine.org/what-is-entropy-a-measure-of-just-how-little-we-really-know-20241213/
Φεβ 06 2025
Η απίστευτη βραδύτητα της ανθρώπινης σκέψης
Σύμφωνα με μια νέα έρευνα που δημοσιεύτηκε στο περιοδικό Neuron, τα ανθρώπινα όντα σκέφτονται με βασανιστικά αργή ταχύτητα, περίπου 10 bit ανά δευτερόλεπτο – θυμούνται, λαμβάνουν αποφάσεις και φαντάζονται τα πράγματα με αυτόν τον ρυθμό. Αντιθέτως, τα ανθρώπινα αισθητήρια συστήματα συγκεντρώνουν δεδομένα με ρυθμό περίπου ένα δισεκατομμύριο bit ανά δευτερόλεπτο. Αυτό το βιολογικό παράδοξο, που τονίζεται στη νέα εργασία, πιθανότατα συμβάλλει στην ψευδή αίσθηση ότι το μυαλό μας μπορεί να εμπλακεί σε φαινομενικά άπειρες σκέψεις ταυτόχρονα – ένα φαινόμενο που οι συγγραφείς της μελέτης θεωρούν ως «η ψευδαίσθηση του Μασκ». Κι αυτό γιατί ο Ίλον Μασκ φιλοδοξεί να συνδέσει τον ανθρώπινο εγκέφαλο με υπολογιστή ώστε να αυξηθεί η ταχύτητα με την οποία λειτουργεί ο εγκέφαλός μας. Φαίνεται ότι κάτι τέτοιο δεν θα γίνει ποτέ πραγματικότητα, αφού οι άνθρωποι σκέφτονται με τον ασήμαντο ρυθμό 10 bit ανά δευτερόλεπτο, τον ρυθμό μιας συνομιλίας.
«Ο ανθρώπινος εγκέφαλος είναι πολύ λιγότερο εντυπωσιακός από όσο πιστεύουμε», λέει ο συν-συγγραφέας της μελέτης Markus Meister, νευροεπιστήμονας στο Caltech. «Είναι απίστευτα αργός όταν πρόκειται για την λήψη αποφάσεων και είναι γελοία πιο αργός από οποιαδήποτε από τις συσκευές με τις οποίες αλληλεπιδρούμε.»
Ο Meister και η συν-συγγραφέας Jieyu Zheng, υποψήφια διδάκτωρ νευροβιολογίας στο Caltech, υποστηρίζουν επίσης ότι ο εγκέφαλός μας μπορεί να κάνει μόνο ένα πράγμα τη φορά. Κι αυτό σιγά-σιγά. Έτσι, ακόμη κι αν ο Μασκ κατάφερνε να συνδέσει τον εγκέφαλό του σε έναν υπολογιστή, λέει ο Meister, δεν θα μπορούσε να επικοινωνήσει μαζί του γρηγορότερα.
Η νέα μελέτη θα μπορούσε να αλλάξει τον τρόπο με τον οποίο οι νευροεπιστήμονες προσεγγίζουν ορισμένα ερωτήματα. Γιατί το περιφερικό μας νευρικό σύστημα μπορεί να επεξεργάζεται χιλιάδες αντικείμενα παράλληλα, αλλά μπορούμε να κάνουμε μόνο ένα πράγμα τη φορά; Οποιαδήποτε θεωρία του εγκεφάλου που επιδιώκει να εξηγήσει όλα τα συναρπαστικά πράγματα που μπορούμε να κάνουμε, όπως ο σχεδιασμός και η επίλυση προβλημάτων, θα πρέπει να εξηγήσει αυτό το παράδοξο.
διαβάστε περισσότερες λεπτομέρειες στο άρθρο με τίτλο «The Unbelievable Slowness of Thinking» – https://www.scientificamerican.com/article/the-human-brain-operates-at-a-stunningly-slow-pace/
Φεβ 06 2025
Τι είναι η πιθανότητα;
Η ζωή είναι αβέβαιη. Κανείς μας δεν ξέρει τι πρόκειται να συμβεί. Γνωρίζουμε ελάχιστα για το τι έχει συμβεί στο παρελθόν ή τι συμβαίνει τώρα πέρα από την άμεση εμπειρία μας. Η αβεβαιότητα ονομάστηκε «συνειδητή επίγνωση της άγνοιας» – είτε πρόκειται για τον αυριανό καιρό, είτε για το αποτέλεσμα του ποδοσφαιρικού αγώνα Ολυμπιακού-Παναθηναϊκού, ή για το αν θα γίνει τις επόμενες ημέρες μεγάλος σεισμός.
Στην καθημερινή ζωή, γενικά εκφράζουμε την αβεβαιότητα με λόγια, λέγοντας ότι ένα γεγονός «θα μπορούσε», «μπορεί» ή «είναι πιθανό» να συμβεί. Αλλά οι αβέβαιες λέξεις μπορεί να είναι ύπουλες. Όταν, το 1961, ο νεοεκλεγείς πρόεδρος των ΗΠΑ Τζον Φ. Κένεντι ενημερώθηκε για ένα σχέδιο εισβολής στην Κούβα υπό την αιγίδα της CIA και ζήτησε μια αξιολόγηση από την ανώτατη στρατιωτική του ομάδα. Κατέληξαν στο συμπέρασμα ότι η αποστολή είχε 30% πιθανότητες επιτυχίας – δηλαδή 70% πιθανότητα αποτυχίας. Στην έκθεση που έφτασε στον πρόεδρο, αυτό αναφερόταν ως «μια καλή ευκαιρία». Έτσι αποφασίστηκε η εισβολή στον Κόλπο των Χοίρων και κατέληξε σε φιάσκο. Σήμερα υπάρχουν καθιερωμένες κλίμακες για την αριθμητική εκτίμηση πιθανοτήτων αβέβαιων γεγονότων. Για παράδειγμα, οποιοσδήποτε στην κοινότητα πληροφοριών του Ηνωμένου Βασιλείου χρησιμοποιεί τον όρο «πιθανό», αυτό θα πρέπει να σημαίνει πιθανότητα μεταξύ 55% και 75% (βλέπε go.nature.com/3vhu5zc).
Ανοίξτε οποιοδήποτε επιστημονικό περιοδικό, για παράδειγμα και θα βρείτε άρθρα που είναι πασπαλισμένα με τιμές σημαντικότητας P, διαστήματα εμπιστοσύνης και πιθανώς εκ των υστέρων Μπεϋζιανές κατανομές, όπου όλα εξαρτώνται από την πιθανότητα.
Κι όμως, οποιαδήποτε αριθμητική πιθανότητα – είτε σε μια επιστημονική εργασία, ως μέρος των μετεωρολογικών προβλέψεων, ή στην πρόβλεψη της έκβασης ενός ποδοσφαιρικού αγώνα ή στον ποσοτικό προσδιορισμό ενός κινδύνου για την υγεία – δεν είναι μια αντικειμενική ιδιότητα του κόσμου, αλλά μια κατασκευή που βασίζεται σε προσωπικές ή συλλογικές κρίσεις και (συχνά αμφίβολες) υποθέσεις. Επιπλέον, στις περισσότερες περιπτώσεις, δεν υπολογίζει καν κάποια υποκείμενη «αληθινή» ποσότητα. Πράγματι, η πιθανότητα σπανιότατα μπορεί να ειπωθεί ότι «υπάρχει».
Η πιθανότητα εισήλθε σχετικά αργά στα μαθηματικά. Αν και οι άνθρωποι έπαιζαν «κόκκαλα» ή ζάρια για χιλιετίες, μόνο όταν οι Γάλλοι μαθηματικοί Blaise Pascal και Pierre de Fermat άρχισαν στη δεκαετία του 1650 την συστηματική ανάλυση των «τυχαίων» γεγονότων. Έκτοτε, η πιθανότητα έχει πλημμυρίσει τομείς τόσο διαφορετικούς όπως η οικονομία, η αστρονομία και η νομική – για να μην αναφέρουμε τον τζόγο.
Για να καταλάβετε την παρανόηση που κρύβεται πίσω από την έννοια της πιθανότητας, σκεφτείτε πώς χρησιμοποιείται η έννοια στις σύγχρονες μετεωρολογικές προβλέψεις. Οι μετεωρολόγοι κάνουν προβλέψεις για την θερμοκρασία, την ταχύτητα του ανέμου και την ποσότητα της βροχής, και πολύ συχνά για την πιθανότητα βροχής – ας πούμε 70% για δεδομένο χρόνο και τόπο. Οι τρείς πρώτες μπορούν να συγκριθούν με τις «αληθινές» τιμές τους. Μπορείτε να βγείτε έξω και να τις μετρήσετε. Αλλά δεν υπάρχει «αληθινή» πιθανότητα να συγκρίνει την τελευταία με την εκτίμηση της πρόγνωσης. Δεν υπάρχει «πιθανόμετρο». Ή βρέχει ή δεν βρέχει.
Επιπλέον, όπως υπογράμμισε ο φιλόσοφος Ian Hacking, η πιθανότητα έχει «το πρόσωπο του Ιανού»: χειρίζεται τόσο την τύχη όσο και την άγνοια. Φανταστείτε ότι ρίχνω ένα νόμισμα και σας ρωτάω ποιά είναι η πιθανότητα να έλθει «κορώνα». Λέτε άνετα «50%». Στη συνέχεια ρίχνω το νόμισμα και πιάνοντάς το με τα δυο μου χέρια στον αέρα. Αφού ρίξω μια γρήγορη κρυφή ματιά στο κέρμα, ξαναρωτάω: ποια είναι η πιθανότητά σας να είναι τώρα «κορώνα»;
Σημειώστε ότι λέω η πιθανότητά «σας», όχι «η» πιθανότητα. Οι περισσότεροι άνθρωποι τώρα διστάζουν να δώσουν μια απάντηση, πριν επαναλάβουν διστακτικά «50–50». Αλλά το γεγονός συνέβη τώρα, και δεν υπάρχει τυχαιότητα – μόνο η άγνοιά σας. Η κατάσταση έχει μετατραπεί από την «τυχαία» αβεβαιότητα, για το μέλλον που δεν μπορούμε να γνωρίζουμε, στην «γνωσιολογική» αβεβαιότητα, γι αυτό που προς το παρόν δεν γνωρίζουμε. Η αριθμητική πιθανότητα χρησιμοποιείται και για τις δύο αυτές καταστάσεις.
Ακόμα κι αν υπάρχει ένα στατιστικό μοντέλο για το τι πρέπει να συμβεί, αυτό βασίζεται πάντα σε υποκειμενικές υποθέσεις – στην περίπτωση ρίψης νομίσματος, ότι υπάρχουν δύο εξίσου πιθανά αποτελέσματα. Όλοι θεωρούμε ότι η ρίψη ενός νομίσματος έχει μοιρασμένες πιθανότητες «50-50» να έρθει κορώνα ή γράμματα, όταν (υποκειμενικά) εμπιστευόμαστε αυτόν που εκτελεί τη ρίψη ότι δεν χρησιμοποιεί ένα νόμισμα π.χ. με δυο κορώνες.
Όποιαδήποτε πρακτική χρήση της πιθανότητας περιλαμβάνει υποκειμενικές κρίσεις. Αυτό δεν σημαίνει ότι μπορώ να επιλέξω οποιουσδήποτε αριθμούς – θα αποδεικνυόμουν κακός εκτιμητής πιθανοτήτων αν ισχυριζόμουν με βεβαιότητα 99,9% ότι μπορώ να πετάξω από τη στέγη μου, για παράδειγμα. Ο αντικειμενικός κόσμος μπαίνει στο παιχνίδι όταν οι πιθανότητες και οι υποκείμενες υποθέσεις τους ελέγχονται έναντι της πραγματικότητας. Αλλά αυτό δεν σημαίνει ότι οι ίδιες οι πιθανότητες είναι αντικειμενικές.
Ορισμένες υποθέσεις που χρησιμοποιούν οι άνθρωποι για να εκτιμήσουν τις πιθανότητες θα έχουν ισχυρότερη αιτιολόγηση από άλλες. Αν έχω εξετάσει προσεκτικά ένα νόμισμα προτού το ρίξω, και προσγειωθεί σε μια σκληρή επιφάνεια και αναπηδά χαοτικά, θα αισθανθώ πιο δικαιωμένος με την κρίση μου 50-50, παρά αν κάποιος άγνωστος μυστηριώδης τύπος ρίξει ένα δικό του νόμισμα περιορίζοντάς το σε μερικές τυχαίες στροφές. Αλλά αυτοί οι ίδιοι περιορισμοί ισχύουν οπουδήποτε χρησιμοποιούνται πιθανότητες – ακόμη και σε επιστημονικά πλαίσια, στα οποία θα μπορούσαμε να είμαστε λιγότερο υποψιασμένοι για την υποτιθέμενη αντικειμενικότητά τους.
Είναι όμως αυτοί οι αριθμοί, οι υποκειμενικές μας, και ίσως εσφαλμένες εκτιμήσεις μας για κάποια υποκείμενη «αληθινή» πιθανότητα, ένα αντικειμενικό χαρακτηριστικό του κόσμου; Πώς ορίζεται στην πραγματικότητα μια αντικειμενική πιθανότητα;
Έχουν γίνει πολλές προσπάθειες για να δοθεί μια απάντηση στο ερώτημα αυτό, αλλά όλες φαίνονται είτε ελαττωματικές είτε περιορισμένες. Αυτές περιλαμβάνουν την πιθανότητα συχνότητας, μια προσέγγιση που ορίζει τη θεωρητική αναλογία γεγονότων που θα μπορούσαν να εμφανιστούν σε άπειρες επαναλήψεις ουσιαστικά πανομοιότυπων καταστάσεων – για παράδειγμα, επανάληψη της ίδιας κλινικής δοκιμής στον ίδιο πληθυσμό με τις ίδιες καταστάσεις ξανά και ξανά, όπως στην ταινία Ημέρα της Μαρμότας. Αυτό φαίνεται μάλλον μη ρεαλιστικό. Ο Βρετανός στατιστικολόγος Ronald Fisher πρότεινε να σκεφτούμε ένα μοναδικό σύνολο δεδομένων ως δείγμα από έναν υποθετικό άπειρο πληθυσμό, αλλά αυτό φαίνεται να είναι περισσότερο ένα πείραμα σκέψης παρά μια αντικειμενική πραγματικότητα. Ή υπάρχει η ημι-μυστικιστική ιδέα της τάσης, ότι υπάρχει κάποια αληθινή υποκείμενη τάση να συμβεί ένα συγκεκριμένο γεγονός σε ένα συγκεκριμένο πλαίσιο, όπως για παράδειγμα να πάθω καρδιακή προσβολή τα επόμενα δέκα χρόνια ή να εκραγεί ένα συγκεκριμένο ηφαίστειο στους επόμενους μήνες. Οι πιθανότητες που αποδίδονται σε τέτοια γεγονότα φαίνονται πρακτικά μη επαληθεύσιμες.
Υπάρχει ένα περιορισμένο εύρος καλά ελεγχόμενων, επαναλαμβανόμενων καταστάσεων με τεράστια πολυπλοκότητα που, ακόμη κι αν είναι ουσιαστικά ντετερμινιστικές, ταιριάζουν με το παράδειγμα συχνότητας, έχοντας μια κατανομή πιθανότητας με προβλέψιμες ιδιότητες μακροπρόθεσμα. Αυτές περιλαμβάνουν τυπικές διατάξεις τυχαιοποίησης, όπως τροχούς ρουλέτας, ανακατεμένες κάρτες, ρίξιμο νομισμάτων, ζαριών και σφαιρίδια λοταρίας, καθώς και γεννήτριες ψευδοτυχαίων αριθμών, που βασίζονται σε μη γραμμικούς, χαοτικούς αλγόριθμους για να δώσουν αποτελέσματα που περνούν τα τεστ τυχαιότητας.
Στον φυσικό κόσμο, π.χ. μπορούμε να θεωρήσουμε την συμπεριφορά πολύ μεγάλου αριθμού μορίων αερίων τα οποία, ακόμα κι αν ακολουθούν τη νευτώνεια φυσική, υπακούουν στους νόμους της στατιστικής μηχανικής. ή στη γενετική, όπου η τεράστια πολυπλοκότητα της επιλογής και του ανασυνδυασμού των χρωμοσωμάτων οδηγεί σε σταθερά ποσοστά κληρονομικότητας. Μπορεί να είναι λογικό σε αυτές τις περιορισμένες περιστάσεις να υποθέσουμε μια ψευδο-αντικειμενική πιθανότητα – αντί για «μια» (υποκειμενική) πιθανότητα.
Ωστόσο, σε κάθε άλλη κατάσταση στην οποία χρησιμοποιούνται πιθανότητες – από μεγάλα τμήματα της επιστήμης μέχρι τον αθλητισμό, την οικονομία, τον καιρό, το κλίμα, την σεισμολογία, την ανάλυση κινδύνου, τα μοντέλα καταστροφών κ.λπ. – δεν έχει νόημα να θεωρούμε ότι οι κρίσεις μας είναι εκτιμήσεις για αληθινές πιθανότητες. Αυτές είναι απλώς καταστάσεις στις οποίες μπορούμε να προσπαθήσουμε να εκφράσουμε την προσωπική ή συλλογική μας αβεβαιότητα ως προς τις πιθανότητες, με βάση τις γνώσεις και την κρίση μας.
Όλα αυτά απλώς εγείρουν περισσότερα ερωτήματα. Πώς ορίζουμε την υποκειμενική πιθανότητα; Και γιατί οι νόμοι των πιθανοτήτων είναι λογικοί, αν βασίζονται σε πράγματα που ουσιαστικά επινοούμε; Αυτό έχει συζητηθεί στην ακαδημαϊκή βιβλιογραφία σχεδόν επί έναν αιώνα, αλλά χωρίς καθολικά αποδεκτό αποτέλεσμα.
O μαθηματικός Bruno de Finetti ξεκινά το βιβλίο του «Θεωρία των Πιθανοτήτων» με την προκλητική δήλωση: οι πιθανότητες δεν υπάρχουν! Παρ’ όλα αυτά υποστήριξε ότι ξεκινώντας από μια συγκεκριμένη, αλλά καθαρά υποκειμενική, έκφραση πεποιθήσεων, θα πρέπει να ενεργούμε σαν τα γεγονότα να οδηγούνται από αντικειμενικές πιθανότητες.
Είναι εκπληκτικό το γεγονός ότι ένα τόσο σημαντικό σύνολο έργου, στο οποίο βασίζεται όλη η στατιστική επιστήμη, όπως και πλήθος επιστημονικών και οικονομικών δραστηριοτήτων, έχει προκύψει από μια τόσο ασαφή ιδέα. Ίσως στον καθημερινό μας κόσμο, οι πιθανότητες πιθανότατα δεν υπάρχουν – αλλά είναι συχνά χρήσιμο να ενεργούμε σαν να υπάρχουν.
διαβάστε περισσότερες λεπτομέρειες στο άρθρο του David Spiegelhalter με τίτλο «Probability Probably Doesn’t Exist» – http://www.scientificamerican.com/article/why-probability-probably-doesnt-exist-but-its-useful-to-act-like-it-does/
Ιαν 23 2025
Αυτά είναι τα 13 επαγγέλματα του μέλλοντος – 170 εκατ. θέσεις εργασίας μέχρι το 2030
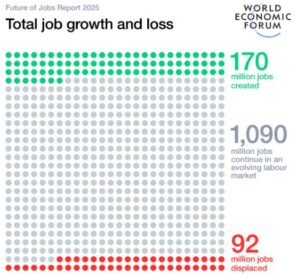
Το Παγκόσμιο Οικονομικό Φόρουμ (WEF) προβλέπει τη δημιουργία 170 εκατομμυρίων νέων θέσεων εργασίας έως το τέλος της δεκαετίας, σύμφωνα με την έκθεσή του για το Μέλλον της Εργασίας 2025. Η έκθεση αναδεικνύει πώς οι τεχνολογικές εξελίξεις, η πράσινη μετάβαση και οι οικονομικές και δημογραφικές αλλαγές αναδιαμορφώνουν την παγκόσμια αγορά εργασίας.
Παρότι οι ίδιες τάσεις θα οδηγήσουν στην απώλεια 92 εκατομμυρίων θέσεων εργασίας, η συνολική αύξηση στην απασχόληση αναμένεται να φτάσει τα 78 εκατομμύρια καθαρές νέες θέσεις εργασίας. Αυτές οι θέσεις αντιστοιχούν στο 14% της σημερινής παγκόσμιας απασχόλησης.
Οι ταχύτερα αναπτυσσόμενοι τομείς
Η ζήτηση για ρόλους που σχετίζονται με την τεχνολογία, όπως ειδικοί δεδομένων, μηχανικοί fintech και ειδικοί στην τεχνητή νοημοσύνη (AI) και μηχανική μάθηση, αυξάνεται ραγδαία. Σε απόλυτους αριθμούς, οι 15 επαγγελματικοί κλάδοι με τη μεγαλύτερη ανάπτυξη περιλαμβάνουν:
- Εργαζόμενοι στη γεωργία: Η πράσινη μετάβαση θα δημιουργήσει 34 εκατομμύρια νέες θέσεις έως το 2030.
- Οδηγοί διανομής, προγραμματιστές λογισμικού, εργαζόμενοι στην οικοδομή και πωλητές: Συμπληρώνουν την πρώτη πεντάδα.
- Εργαζόμενοι στη μεταποίηση τροφίμων και στον τομέα της φροντίδας: Οι νοσηλευτές, κοινωνικοί λειτουργοί και σύμβουλοι αναμένεται να γνωρίσουν σημαντική αύξηση λόγω της γήρανσης του πληθυσμού.
Μέχρι το 2030, το 39% των βασικών δεξιοτήτων στην αγορά εργασίας θα έχει αλλάξει. Παρά τη μείωση σε σχέση με το 44% του 2023, η ανάγκη για αναβάθμιση και επανεκπαίδευση παραμένει κρίσιμη.
 Οι δεξιότητες που θα αυξήσουν τη σημασία τους περιλαμβάνουν:
Οι δεξιότητες που θα αυξήσουν τη σημασία τους περιλαμβάνουν:
- Τεχνολογικές δεξιότητες: Τεχνητή νοημοσύνη, μεγάλα δεδομένα, κυβερνοασφάλεια και τεχνολογικός εγγραμματισμός.
- Δημιουργική σκέψη, ανθεκτικότητα και ευελιξία: Η διαρκής περιέργεια και μάθηση θεωρούνται πλέον απαραίτητες.
- Ηγεσία, κοινωνική επιρροή και διαχείριση ταλέντων: Συμπληρώνουν τις βασικές δεξιότητες για το μέλλον.
Οι επιχειρήσεις επενδύουν όλο και περισσότερο σε προγράμματα αναβάθμισης και επανεκπαίδευσης για να ανταποκριθούν στις νέες απαιτήσεις. Το WEF, μέσω των πρωτοβουλιών Jobs Initiative και Reskilling Revolution, συνεργάζεται με επιχειρήσεις, ακαδημαϊκούς και κυβερνήσεις για να προετοιμάσει τους εργαζόμενους για την οικονομία του αύριο.
Επαγγέλματα με τη μεγαλύτερη αύξηση και μείωση έως το 2030
- Κτηνοτρόφοι, εργάτες και άλλοι αγροτικοί εργαζόμενοι
- Οδηγοί ελαφρών φορτηγών ή υπηρεσιών διανομής
- Προγραμματιστές λογισμικού και εφαρμογών
- Οικοδόμοι
- Πωλητές καταστημάτων
- Εργαζόμενοι στη μεταποίηση τροφίμων και σχετικών επαγγελμάτων
- Οδηγοί αυτοκινήτων, βαν και μοτοσυκλετών
- Νοσηλευτές και επαγγελματίες υγείας
- Εργαζόμενοι σερβιρίσματος φαγητού και ποτών
- Γενικοί και επιχειρησιακοί διευθυντές
- Επαγγελματίες κοινωνικής εργασίας και συμβουλευτικής
- Διαχειριστές έργων (project managers)
- Καθηγητές πανεπιστημίου και ανώτατης εκπαίδευσης
Επαγγέλματα με τη μεγαλύτερη μείωση
- Ταμίες και υπάλληλοι εισιτηρίων
- Διοικητικοί βοηθοί και εκτελεστικοί γραμματείς
- Οικονόμοι, καθαριστές και φροντιστές κτιρίων
- Υπάλληλοι καταγραφής υλικών και αποθήκης
- Εργαζόμενοι σε εκτυπώσεις και σχετικές εργασίες
- Υπάλληλοι λογιστικής, μισθοδοσίας και τήρησης βιβλίων
- Λογιστές και ελεγκτές
- Συνοδοί μεταφορών και ελεγκτές
- Φύλακες ασφαλείας
- Υπάλληλοι τραπεζών και σχετικών κλάδων
- Υπάλληλοι καταχώρισης δεδομένων
- Υπάλληλοι πληροφοριών πελατών και εξυπηρέτησης
- Γραφίστες
Νοέ 28 2024
Οι εγκύκλιοι για την υποβολή Αίτησης–Δήλωσης για συμμετοχή στις Πανελλαδικές Εξετάσεις
Από Παρασκευή 29-11-2024 ως και Παρασκευή 20-12-2024 για όλους τους υποψηφίους που επιθυμούν να συμμετάσχουν στις Πανελλαδικές εξετάσεις
- Πατήστε εδώ γα να ανοίξετε την εγκύκλιο για τα ΓΕΛ
- Πίνακας με τις Ομάδες προσανατολισμού, τα Επιστημονικά Πεδία και τα Εξεταζόμενα Μαθήματαμε τα πανελλαδικώς εξεταζόμενα μαθήματα
- Υπόδειγμα Αίτησης – Δήλωσης Μαθητή/τριας ή Αποφοίτου για τα ΓΕΛ
- Αναλυτικές Οδηγίες Συμπλήρωσης της Αίτησης
- Αίτηση – Υπεύθυνη Δήλωση για τα 5 Μουσικά Τμήματα των ΑΕΙ με την ειδική διαδικασία εισαγωγής ΓΕΛ 2025
- Κατάλογος Μουσικών Οργάνων για το εξεταζόμενο μάθημα “Μουσική Εκτέλεση και Ερμηνεία”











