23/11 Παγκόσμια Ημέρα Φιμπονάτσι – Happy Fibonacci Day!

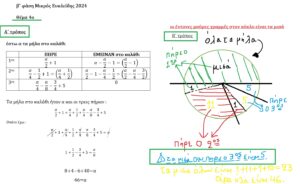
Σήμερα 23/11 ή όπως γράφεται στο εξωτερικό (μήνας πρώτα) 11/23 είναι η Παγκόσμια ημέρα Φιμπονάτσι (mathholiday),

μιας και η ημερομηνία θυμίζει τη γνωστή ακολουθία :

1, 1, 2, 3, 5, 8, 13, 21, 34, 55 , 89 , ……………….

Βασίζεται στο πρόβλημα που μελέτησε και τον οδήγησε μάλλον τυχαία  στον ορισμό της ακολουθίας του, αφορούσε την αναπαραγωγή κουνελιών. Το έθεσε στο ιστορικό βιβλίο του Liber Abaci (βιβλίο των υπολογισμών) που δημοσιεύθηκε για πρώτη φορά το 1202.

Πρόβλημα

“Σε ένα σπίτι στο χωριό γεννιέται ένα ζευγάρι κουνέλια. Τα κουνέλια αυτά χρειάζονται 2 μήνες για να μεγαλώσουν και να αρχίσουν να γεννούν. Έτσι μετά από δύο μήνες το ζευγάρι αυτό γεννά ένα νέο ζευγάρι στην αρχή κάθε μήνα. Τα νέα ζευγάρια μεγαλώνουν και αναπαράγονται κι αυτά με τον ίδιο τρόπο. Πόσα ζευγάρια κουνέλια θα έχουμε μετά από 3 μήνες, 4 μήνες, 6 μήνες, μετά από ένα χρόνο;”

Απάντηση

• Στην αρχή του πρώτου μήνα έχουμε 1 ζευγάρι κουνέλια
• Στην αρχή του δεύτερου μήνα έχουμε πάλι 1 ζευγάρι
• Στην αρχή του τρίτου μήνα το αρχικό ζευγάρι γεννά και έχουμε συνολικά 2 ζευγάρια κουνέλια
• Στην αρχή του τέταρτου μήνα το πρώτο ζευγάρι γεννά πάλι , αλλά το δεύτερο δεν είναι σε θέση ακόμη, συνολικά 3 ζευγάρια.
• Στην αρχή του πέμπτου μήνα γεννά πάλι το αρχικό ζευγάρι , γεννά και το δεύτερο , δε γεννά το τρίτο. Σύνολο 5 ζευγάρια.

Έτσι, το πλήθος των ζευγαριών των κουνελιών στην αρχή κάθε μήνα είναι 1, 1, 2, 3, 5, 8, 13, 21, 34, ..

Παρατηρήστε ότι κάθε αριθμός στην ακολουθία είναι το άθροισμα των δύο προηγούμενων. Αυτό είναι λογικό να συμβαίνει μια και στην αρχή κάθε μήνα έχουμε τα ζευγάρια που είχαμε τον προηγούμενο μήνα και επιπλέον τόσα νεογέννητα ζευγάρια όσα και ενήλικα ζευγάρια γονέων έχουμε.

Άρα οι αριθμοί Fibonacci είναι: 1,1,2,3,5,8,13,21,34,55,89,…..  με τον κάθε αριθμό να προκύπτει από το άθροισμα των δύο προηγούμενων του.

1+1=2 , 1+2=3 , 3+5=8 , 5+8=13 ,…..

Περισσότερα μπορείτε να βρείτε,

• εδώ , στην σελίδα του συνάδερφου κ.Αθ. Δρούγα , προσπελάστηκε 23.11.17 και ώρα 13:20 και
• ΕΔΩ ένα άρθρο απ τον αγαπητό συνάδερφο κ. Αθ. Κοπάδη απ το οποίο είναι και τα παραπάνω ιστορικά στοιχεία.

Happy Fibonacci day to all !

Copyright © 2024. Με την επιφύλαξη όλων των δικαιωμάτων.