Τσαρλς Σπένσερ Τσάπλιν ή Τσάρλι Τσάπλιν. Από τους πιο γνωστούς κινηματογραφικούς «αστέρες» πριν το τέλος του Πρώτου Παγκοσμίου Πολέμου, γνωστός και ως «Σαρλό» (κωμικό-τραγικός τύπος με φαρδιά παντελόνια, κοντό μουστάκι, τρύπια παπούτσια και το χαρακτηριστικό μπαστούνι που ο ίδιος δημιούργησε).

Γιος οικογένειας ηθοποιών, ο Τσάπλιν ανέβηκε στο σανίδι σε ηλικία μόλις πέντε ετών, ενώ μικρός γνώρισε τη φτώχεια και την εξαθλίωση στις συνοικίες του Ανατολικού Λονδίνου.

Σε νεαρή ηλικία μεταβαίνει στις ΗΠΑ όπου ξεκινά μια σημαντική κινηματογραφική καριέρα, που θα δώσει κλασικά, πλέον αριστουργήματα, όπως «Μοντέρνοι Καιροί», «Ο κύριος Βερντού», «Τα Φώτα της Πόλης», «Ο Μεγάλος Δικτάτωρ» κλπ.

Οι αντιδράσεις που προκαλεί με τον «Κύριο Βερντού», όπου καυτηριάζει το βιομηχανικό- και όχι μόνο- κατεστημένο των ΗΠΑ, τον αναγκάζει να αυτοεξοριστεί στην Ελβετία.

Παντρεύτηκε τέσσερις φορές- και τις τέσσερις με ηθοποιούς- και απέκτησε 11 παιδιά. Αφησε

την τελευταία του πνοή στις 25 Δεκεμβρίου 1977- και ένα σημαντικό έργο πίσω του.

 Α  ΛΥΚΕΙΟΥ

http://www.mathsforyou.gr/a_lykeiou/02.pdf

http://www.mathsforyou.gr/a_lykeiou/01.pdf

http://www.mathsforyou.gr/a_lykeiou/03.pdf          http://www.mathsforyou.gr/a_lykeiou/04.pdf http://www.kee.gr/attachments/file/277.pdf Β ΛΥΚΕΙΟΥ  http://www.mathsforyou.gr/b_lykeiou/01.pdf http://www.mathsforyou.gr/b_lykeiou/02.pdf  http://www.mathsforyou.gr/b_lykeiou/05.pdf  http://www.mathsforyou.gr/b_lykeiou/06.pdf http://www.kee.gr/attachments/file/1960.pdf  http://www.mathsforyou.gr/b_lykeiou/09.pdf Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΑ ΘΕΜΑΤΑ ΑΝΑΛΥΣΗΣ.pdf

ΔΙΑΓΩΝΙΣΜΑ

diagwnisma.pdf ΕΜΒΑΔΟ ΕΠΙΠΕΔΟΥ ΧΩΡΙΟΥ ΜΙΓΑΔΙΚΟΙ ΤΥΠΟΛΟΓΙΟ - ΙΔΙΟΤΗΤΕΣ παραγώγων, παραγουσών, ολοκληρωμάτων download pdf ΕΔΩ  ΘΕΤΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Θέματα Πανελλαδικών 2009 Φυσική Θετικής Κατεύθυνσης Φυσική 2009 Μαθηματικά Θετικής Κατεύθυνσης Μαθηματικά 2009 Χημεία Θετικής Κατεύθυνσης Χημεία 2009 Βιολογία Θετικής Κατεύθυνσης Βιολογία 2009 Θέματα Πανελλαδικών 2008 Φυσική Θετικής Κατεύθυνσης  Φυσική 2008 Μαθηματικά Θετικής Κατεύθυνσης  Μαθηματικά 2008 Χημεία Θετικής Κατεύθυνσης  Χημεία 2008 Βιολογία Θετικής Κατεύθυνσης  Βιολογία 2008 Θέματα Πανελλαδικών 2007 Φυσική Θετικής Κατεύθυνσης  Φυσική 2007 Μαθηματικά Θετικής Κατεύθυνσης  Μαθηματικά 2007 Χημεία Θετικής Κατεύθυνσης  Χημεία 2007  ΘΕΩΡΗΤΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Θέματα Πανελλαδικών 2009 Αρχαία Θεωρητικής Κατεύθυνσης Αρχαία 2009 Λατινικά Θεωρητικής Κατεύθυνσης Λατινικά 2009 Νεοελληνική Λογοτεχνία Θεωρητικής Κατεύθυνσης Λογοτεχνία 2009 Ιστορία Θεωρητικής Κατεύθυνσης Ιστορία 2009 Θέματα Πανελλαδικών 2008 Αρχαία Θεωρητικής Κατεύθυνσης  Αρχαία 2008 Λατινικά Θεωρητικής Κατεύθυνσης  Λατινικά 2008 Νεοελληνική Λογοτεχνία Θεωρητικής Κατεύθυνσης  Νεοελληνική Λογοτεχνία 2008 Ιστορία Θεωρητικής Κατεύθυνσης Ιστορία 2008 Θέματα Πανελλαδικών 2007 Αρχαία Θεωρητικής Κατεύθυνσης  Αρχαία 2007 Λατινικά Θεωρητικής Κατεύθυνσης  Λατινικά 2007 Νεοελληνική Λογοτεχνία Θεωρητικής Κατεύθυνσης  Νεοελληνική λογοτεχνία 2007 Ιστορία Θεωρητικής Κατεύθυνσης  Ιστορία 2007 Αναζήτηση θεμάτων πανελλαδικώς εξεταζομένων μαθημάτων

Ευκλείδης Ο Θεμελιωτής της Γεωμετρίας Τρίτη 13 Ιουλίου 2004 11:37  [Σχόλια: 26, Hits: 1] Για τη ζωή του Ευκλείδη είναι γνωστά λίγα πράγματα: ήταν σύγχρονος του Αρχιμήδη και πιθανόν να μαθήτευσε στην Ακαδημία του Πλάτωνα στην Αθήνα. Κατά την κυριαρχία του Πτολεμαίου Α’ στην Αλεξάνδρεια ίδρυσε ο Ευκλείδης μία Σχολή. Άλλες αξιόλογες τεκμηριωμένες πληροφορίες δεν υπάρχουν.   Το κυριότερο σύγγραμμα του Ευκλείδη, υπό τον τίτλο «Στοιχεία» που υποδιαιρείται σε 13 βιβλία, αποτελεί το σπουδαιότερο έργο των αρχαιοελληνικών Μαθηματικών και είναι ακόμα η βάση των σχολικών Μαθηματικών. Σ’ αυτό το σύγγραμμά του παρουσιάζει ο Ευκλείδης, με σύντομη και ακριβή μορφή μία συστηματική, απαγωγική- αξιωματική σύνοψη και προσαρμογή όλων των προευκλείδιων μαθηματικών γνώσεων, τις οποίες συμπλήρωσε με θεωρήματα δικά του και άλλα συγχρόνων του Μαθηματικών. Τα πρώτα έξι βιβλία καλύπτουν τη Γεωμετρία του επιπέδου, τα βιβλία επτά μέχρι εννέα την Αριθμητική και τη Θεωρία Αριθμών. Το δέκατο βιβλίο αναφέρεται στους άρρητους αριθμούς και τα τρία τελευταία βιβλία στη Στερεομετρία.   Η Γεωμετρία του Ευκλείδη απετέλεσε το θεμέλιο για την ανάπτυξη της «δυτικής» επιστήμης και τεχνικής και σ’ αυτή τη Γεωμετρία στηρίζονται οι προϋποθέσεις της κλασικής Φυσικής από την Αναγέννηση και μετά. Μόλις το 19ο αιώνα διαπιστώθηκε όμως (Λάμπερτ, Γκάους, Μπολυάι, Λομπατσέβσκι κ.ά.) ότι η ευκλείδεια Γεωμετρία στηρίζεται στην απλοϊκή αντίληψη του επίπεδου χώρου, ο οποίος είναι μεν χρήσιμος για την περιοχή που αντιλαμβάνεται με τις αισθήσεις του ένας άνθρωπος, αλλά όχι για πολύ μεγάλες τιμές των φυσικών μεγεθών (αποστάσεις, ταχύτητες, μάζες κτλ.) Τότε παύει να ισχύει η επίπεδη αντίληψη και μαζί της η ευκλείδεια Γεωμετρία, επειδή στην πραγματικότητα ο χώρος είναι κυρτός! Έτσι η Γεωμετρία συμπληρώνεται με βάση αντιλήψεις που στηρίζονται στον υπερβολικό, ελλειπτικό κ.ά. χώρο.   Η πρώτη επιστημονική προσέγγιση των οπτικών φαινομένων, από μαθηματική άποψη, γίνεται από τον Ευκλείδη, τον 4ο π.χ. αιώνα, μέσα από τις προτάσεις που διατυπώνει και αποδεικνύει στην Οπτική του. Στην μελέτη αυτή ο Ευκλείδης συγκεντρώνει και καταγράφει όλες τις μέχρι τότε εμπειρικές γνώσεις γύρω από την οπτική αντίληψη και επιχειρεί μία γεωμετρική ερμηνεία των οπτικών φαινομένων.   O Ευκλείδης ήταν ο πρώτος που έδωσε τον ορισμό της έννοιας γραμμή τον 3ο αιώνα π.X. Ο ορισμός του Ευκλείδη ήταν ο παρακάτω: γραμμή είναι μήκος απλατές, δηλαδή ένα γεωμετρικό αντικείμενο που έχει μήκος αλλά δεν έχει πλάτος. Ο ορισμός αυτός ήταν ο μοναδικός που είχαν οι μαθηματικοί για 1.850 περίπου χρόνια.

Η σελίδα αυτή εκτυπώθηκε από το site http://www.focusmag.gr.
© 2002 Εκδόσεις Λυμπέρη. Supported by Atcom Internet and Multimedia S.A. Hosted by LiBECOM AE.

 

Στα ίχνη του Πυθαγόρα
[Η ανακάλυψη και η αποδοχή του μηδενός μέσα από μια αφήγηση που διατρέχει τους αιώνες]

Η απόδοση μαγικών και υπερφυσικών δυνάμεων στους αριθμούς είναι σύμφυτη με την ανακάλυψη και τη μετεξέλιξή τους μέσα στον χρόνο. Εν τούτοις ο στοχαστής που ανήγαγε τη μελέτη των ιδιοτήτων τους σε αληθινή λατρεία, οι απόηχοι της οποίας παραμένουν αντιληπτοί για πολλούς αιώνες αργότερα, ήταν αναμφίβολα ο Πυθαγόρας. Την πορεία του σάμιου φιλοσόφου, από την ανάπτυξη της μυστικιστικής θεωρίας του για τον κόσμο των αριθμών ως τον θάνατό του και τη διάλυση της σχολής του, αλλά και την τύχη της σκέψης του κατά τους πρώτους αιώνες της επικράτησης του χριστιανισμού ανασυνθέτει με ιστορικοφανή, πλην ουσιαστικά μυθιστορηματικό, τρόπο ο Αλαίν Ναντώ, καθηγητής Φιλοσοφίας στο Παρίσι. Το αναπάντεχο μα και πιο ενδιαφέρον σημείο αυτής της αρχαιολογικής ανασύνθεσης είναι ότι ενώ το μεγαλύτερο μέρος της καταλαμβάνουν το πρόσωπο και οι ιδέες του Πυθαγόρα, το πραγματικό θέμα της έγκειται σε αυτό που ο έλληνας φιλόσοφος δεν μπόρεσε ή δεν άντεξε να ανακαλύψει: τη μαθηματική και φιλοσοφική σημασία του τίποτε, του μη υπαρκτού, δηλαδή την απουσία που υποδηλώνεται με τη χρήση του συμβόλου «μηδέν».

Για να προσδώσει αληθοφάνεια και πειστικότητα στο εγχείρημά του ο συγγραφέας επιλέγει την αφηγηματική τεχνική της παράθεσης υποτιθέμενων πραγματικών στοιχείων, τα οποία συνθέτουν ένα παζλ από μαρτυρίες που φωτίζουν το θέμα από διαφορετικές και ενίοτε αλληλοσυγκρουόμενες οπτικές γωνίες. Το αφηγηματικό εύρημα έγκειται εδώ στην ανακάλυψη, στα έγκατα του σπιτιού ενός αρχαιολόγου στη δυτική Αλεξάνδρεια, ενός μεγάλου υπόγειου τάφου και στην ανεύρεση μιας σειράς χειρογράφων, πνευματική διαθήκη μιας ιδιόρρυθμης μυστικιστικής σέκτας με την επονομασία “Οι Λάτρεις του Μηδενός“. Το βιβλίο που διαβάζουμε είναι η παράθεση με χρονολογική σειρά των κειμένων αυτών ­ τεκμήρια τα ονομάζει ο συγγραφέας ­, 25 τον αριθμό, συνοδευομένων από ορισμένα διευκρινιστικά σχόλια που αφορούν τον συντάκτη ή τις πιθανές συνθήκες κάτω από τις οποίες γράφτηκε το εκάστοτε τεκμήριο.

Το πρώτο μισό των κειμένων είναι εξ ολοκλήρου αφιερωμένο στον Πυθαγόρα, στην επίσκεψή του στην Αίγυπτο, στη μύησή του στα αιγυπτιακά μαθηματικά, στην επιρροή που άσκησε επάνω του ο εβραϊκός μονοθεϊσμός. Στη συνέχεια παρατίθενται στοιχεία για την ίδρυση της σχολής του, τα παρακλάδια της, τον ρόλο του στα πολιτικά πράγματα του τόπου του και την αποτυχημένη προσπάθειά του να εγκαθιδρύσει ένα τέλειο κοινωνικό σύστημα εμπνευσμένο από την αρμονία του κόσμου των αριθμών. Η αφήγηση σχετικά με τη ζωή του Πυθαγόρα κλείνει με την τελευταία του εκμυστήρευση προς τους μαθητές του, στην οποία ο φιλόσοφος, καταπτοημένος από την εξορία και την αρρώστια, εμφανίζεται να αναγνωρίζει την ύπαρξη του μηδενός και τη σημασία του για την ισορροπία στο Σύμπαν και στην ανθρώπινη ζωή.

Το δεύτερο μισό του βιβλίου επικεντρώνεται στην Αλεξάνδρεια. Μέσα από ποικίλες αφηγήσεις που καλύπτουν τους πρώτους μετά Χριστόν αιώνες παρουσιάζεται με ανάγλυφο τρόπο η πνευματική πορεία της πόλης σε σχέση τόσο με τον ελληνικό όσο και με τον αραβικό πολιτισμό. Η βίαιη καταστολή όλων των παγανιστικών θρησκειών από τις φανατισμένες χριστιανικές ορδές θα οδηγήσει τις διάφορες πυθαγόρειας εμπνεύσεως σέκτες στη συρρίκνωση και στον αφανισμό, όπως συνέβη τελικά και με την παράξενη οργάνωση Οι Λάτρεις του Μηδενός. Οι μύστες της, όπως το μαρτυρεί και το όνομά τους, ήταν άθεοι και υλιστές, λάτρευαν δε το μηδέν ως τον πλέον ξεχωριστό αριθμό, αφού σε αυτόν έβλεπαν να αποτυπώνεται η χαώδης λειτουργία του κόσμου.

Ο Ναντώ, ακολουθώντας τα ιστορικά γεγονότα και την εξέλιξη των διαφόρων φιλοσοφικών και θρησκευτικών ρευμάτων, καταφέρνει να χαράξει τη δύσκολη και συχνά οδυνηρή πορεία του ανθρώπινου πνεύματος από την ακραιφνώς υπερβατική σκέψη σε μια αντίληψη της ζωής κατά την οποία ο θάνατος αποτελεί αναπόσπαστο κομμάτι της. Συνθέτει έτσι, ανατρέχοντας στο παρελθόν και ειδικότερα στην εποχή της παρακμής της Αλεξάνδρειας, μια αλληγορία των περιπετειών της μοντέρνας συνείδησης, έναν καθρέφτη του σύγχρονου κόσμου. Ταυτόχρονα, με την αποστασιοποίηση που του χαρίζει η αφηγηματική μέθοδός του, προτείνει μια στάση ζωής που εμπεριέχει την ίδια την άρνησή της, μια νέα λατρεία του μηδενός που αντιτίθεται σε κάθε προσπάθεια εξωραϊσμού του κόσμου, μια «θρησκεία» της κατάφασης και της αποδοχής του κενού.

Ο κ. Κώστας Κατσουλάρης είναι συγγραφέας. Από τις Εκδόσεις της Εστίας κυκλοφορεί το μυθιστόρημά του «Το σύνδρομο της Μαργαρίτας».
πηγή:ΚΩΣΤΑΣ ΚΑΤΣΟΥΛΑΡΗΣ-Το ΒΗΜΑ

       

Η ιστορία της Τριγωνομετρίας

Ανδρέας Ιωάννου Κασσέτας

 

Η ιστορία της Τριγωνομετρίας αρχίζει με τις πρώτες μαθηματικές καταγραφές στην Αίγυπτο και στη Βαβυλώνα. Οι Βαβυλώνιοι καθιέρωσαν τη μέτρηση των γωνιών σε μοίρες σε πρώτα λεπτά και σε δεύτερα. Οι Βαβυλώνιοι αστρονόμοι είχαν συγκεντρώσει έναν τεράστιο αριθμό δεδομένων από παρατηρήσεις και είναι σήμερα γνωστό ότι ένα μεγάλο μέρος πέρασε στους Έλληνες. Αυτά τα πρώτα βήματα στην Αστρονομία  οδήγησαν και στη γέννηση της Τριγωνομετρίας.

 

Στη σκιά της Αστρονομίας. Η ΧΟΡΔΗ των Ελλήνων  .

Μέχρι όμως την εποχή των Ελλήνων  καμία καθαρά τριγωνομετρική έννοια δεν είχε κάνει  την εμφάνισή της. Και αυτό καθυστέρησε να γίνει και έγινε εξ αρχής σε σύνδεση με την Αστρονομία.

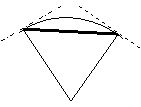Τον δεύτερο αιώνα πριν από τον Χριστό ο αστρονόμος

Ίππαρχος συνέταξε ένα τριγωνομετρικό πίνακα για την επίλυση

τριγώνων. Στον πίνακα αυτόν σε κάθε γωνία απέδιδε μία τιμή που ήταν

 « το μήκος της χορδής» η οποία  αντιστοιχούσε στη γωνία όταν

την έκανε επίκεντρη με σταθερή ακτίνα r.

 Χρειάζεται εδώ να τονίσουμε ότι κανένα έργο του Ίππαρχου δεν έχει διασωθεί και οι γνώσεις μας για το έργο του προέρχονται από μεταγενέστερους συγγραφείς όπως ο Θέων από την Αλεξάνδρεια ο σχολιαστής του 4^ου αιώνα

Δεν γνωρίζουμε ποια ήταν η σταθερή τιμή που έδινε ο  Ίππαρχος στην ακτίνα, αλλά 300 χρόνια αργότερα ο Πτολεμαίος στην Αλμαγέστη χρησιμοποίησε για την ακτίνα του κύκλου την τιμή r = 60 και συνέταξε έναν παρόμοιο πίνακα με ΧΟΡΔΕΣ μία τιμή χορδής για κάθε γωνία από 1 μοίρα μέχρι τις 180⁰ .  Στο ίδιο εγχειρίδιο παρουσίασε και το λεγόμενο θεώρημα του Μενελάου για την επίλυση σφαιρικών τριγώνων. Στους αιώνες που ακολούθησαν η τριγωνομετρία του Πτολεμαίου ήταν η πρωταρχική εισαγωγή για όποιον ήθελε να μυηθεί στην αστρονομία.

Η εξαφάνιση τόσων και τόσων εργασιών των Ελλήνων πάνω στην αστρονομία και την τριγωνομετρία οφείλεται και στο γεγονός ότι η Αλμαγέστη του Πτολεμαίου επεσκίασε όλες τις παλαιότερες εργασίες καθιστώντας τες περιττές

 

Στη σκιά της Αστρονομίας. Το ΗΜΙΤΟΝΟ των Ινδών

Την ίδια περίπου εποχή με τον Πτολεμαίο οι ΙΝΔΟΙ αστρονόμοι είχαν αναπτύξει την σύνταξη τριγωνομετρικών πινάκων ένα τριγωνομετρικό σύστημα βασιζόμενο

όχι στο μήκος της χορδής αλλά στη συνάρτηση του ΗΜΙΤΟΝΟΥ.

Το ημίτονο των Ινδών δεν ήταν  βέβαια καθαρός αριθμός,

όπως είναι σήμερα, αλλά το μήκος της κάθετης πλευράς

ενός ορθογωνίου τριγώνου με σταθερή υποτείνουσα. Και δεν είχαν αποδεχθεί μία ορισμένη τιμή για το μήκος της υποτείνουσας.    

Στο μεταξύ οι Κινέζοι αστρονόμοι του Μεσαίωνα μελετώντας αστρονομία προσέγγισαν τις τριγωνομετρικές έννοιες και εισήγαγαν την τριγωνομετρική εφαπτομένη. Το ενδιαφέρον τους όμως περιορίστηκε σε αστρονομικές εφαρμογές

 

Τριγωνομετρία των Αράβων

Τον 8^ο αιώνα οι Άραβες αστρονόμοι κληρονόμησαν τόσο την ελληνική όσο την ινδική παράδοση

Τα έργα τόσο των Ινδών όσο και των Ελλήνων μεταφράστηκαν και διαβάστηκαν από τους μουσουλμάνους μαθηματικούς οι οποίοι χρησιμοποίησαν το ινδικό ημίτονο παράλληλα με την ελληνική χορδή. Ο Muhammad ibn Jabir al–Battani. εισήγαγε και το συνημίτονο. Αργότερα επανεισήγαγαν την εφαπτομένη των Κινέζων, ενώ  πρότειναν και τη συνεφαπτομένη

Στο τέλος του 10^ου αιώνα χρησιμοποιούσαν πλέον όλες τις τριγωνομετρικές έννοιες, ενώ είχαν ανακαλύψει αλλά και αποδείξει βασικά θεωρήματα της τριγωνομετρίας τόσο για τα επίπεδα όσο και για τα σφαιρικά τρίγωνα. Στο μεταξύ διάφοροι μαθηματικοί πρότειναν για την ακτίνα r του κύκλου την τιμή r = 1 αντί για την r = 60. Όλες αυτές οι ανακαλύψεις είχαν πυροδοτηθεί και από την ανάγκη για την ανάπτυξη της αστρονομίας αλλά και από την ανάγκη προσανατολισμού σε κάθε τόπο και τον προσδιορισμό του «προς τα που» βρίσκεται η Μέκκα προς την κατεύθυνση της οποίας έπρεπε να κοιτάζει ο πέντε φορές την ημέρα  προσευχόμενος μουσουλμάνος. Οι Άραβες ερευνητές συνέταξαν πίνακες εκπληκτικής ακρίβειας με τις τιμές του ημίτονου και της εφαπτομένης για γωνίες ανά  ένα πρώτο λεπτό της μοίρας. Τελικά ο μεγάλος αστρονόμος Nasir ad–Din at– Tusi έγραψε το βιβλίο των το οποίο ήταν το πρώτο δοκίμιο που «είδε» την  επίπεδη και τη σφαιρική τριγωνομετρία ως ανεξάρτητα μαθηματικά αντικείμενα.   

 

Οι Ευρωπαίοι. Γεωγραφία και Αστρονομία

Οι Λατίνοι της δυτικής Ευρώπης γνώρισαν τη μουσουλμανική τριγωνομετρία μέσα από τις μεταφράσεις των αραβικών  αστρονομικών εγχειριδίων, τον 12^ο αιώνα. 

Ο  Richard of Wallingford ήταν ο πρώτος που συσχέτισε το ΙΝΔΙΚΟ ΗΜΙΤΟΝΟ με την Ελληνική ΧΟΡΔΗ και χρησιμοποίησε τα Στοιχεία του Ευκλείδη για την απόδειξη θεωρημάτων τριγωνομετρικών.

Τον 16^ο αιώνα η τριγωνομετρία ενσωματώθηκε στη Γεωγραφία ενώ ήταν ήδη εργαλείο της Αστρονομίας. Η γνώση τριγωνομετρίας ήταν αναγκαία για τον προσδιορισμό της θέσης πάνω στη Γη σε συνδυασμό με τις έννοιες γεωγραφικό πλάτος και γεωγραφικό μήκος

Το πρώτο σημαντικό ευρωπαϊκό έργο γράφτηκε από τον γερμανό αστρονόμο  Regiomontanus ο οποίος στα μέσα του 14^ου αιώνα. μελέτησε την επίπεδη τριγωνομετρία και απέδειξε το θεώρημα των ημίτονων.

Τον επόμενο αιώνα ο επίσης γερμανός αστρονόμος Rheticus

εισήγαγε τη σύγχρονη προσέγγιση των τριγωνομετρικών αριθμών. Μετά από αυτόν κάθε τριγωνομετρική ποσότητα – ημίτονο, συνημίτονο – δεν ήταν πλέον κάποιο μήκος αλλά ένας  ΛΟΓΟΣ δύο μηκών, σε κάθε δηλαδή γωνία αντιστοιχούσε ένας αριθμός .

Κατά τα τέλη του 16^ου αιώνα ο Γάλλος François Viète εμπλούτισε τη σφαιρική τριγωνομετρία, ενώ ο σύγχρονός του  σκωτσέζος John Napier, ο οποίος ανακάλυψε και τους λογαρίθμους, στην αυγή του 17^ου αιώνα πρότεινε δέκα μνημονικούς κανόνες για την επίλυση σφαιρικών τριγώνων.

 

Στην αγκαλιά της ευρωπαϊκής ΑΝΑΛΥΣΗΣ

Πενήντα περίπου χρόνια μετά τη δημοσίευση  των λογαριθμικών πινάκων από τον Napier ο Newton ανακάλυψε τον Calculus παρουσίασε πολλές συναρτήσεις του x ως ΣΕΙΡΕΣ δυνάμεων του x με άπειρους όρους . Ανάμεσα σε αυτές παρουσίασε και τις συναρτήσεις του ημιτόνου sin(x) του συνημιτόνου cos(x) και της εφαπτομένης tan(x) ως ΣΕΙΡΕΣ.

Με την ανακάλυψη του Calculus, τη μελέτη των τριγωνομετρικών συναρτήσεων ανέλαβε η ΑΝΑΛΥΣΗ και οι τριγωνομετρικές συναρτήσεις ξέφυγαν οριστικά από την κηδεμονία της Αστρονομίας και της Γεωγραφίας  και άρχισαν να παίζουν έναν απρόβλεπτα σημαντικό ρόλο τόσο για τα καθαρά όσο και για τα εφαρμοσμένα μαθηματικά.

Τον 18^ο αιώνα με την ευθύνη του Leonhard Euler έγινε η καθόλου προκαθορισμένη συνάντηση των τριγωνομετρικών συναρτήσεων με την εκθετική συνάρτηση και με τους μιγαδικούς αριθμούς ενώ και η εκθετική συνάρτηση περίμενε στη γωνία

         (συνφ + iημφ)ⁿ = συνnφ + iημnφ         e^ix = συνx + iημx 

 

 

 

Σύντομο οδοιπορικό στα μαθηματικά της αρχαίας Ελλάδας

Στα παράλια της Μ. Ασίας είναι που συναντάμε τους πρώτους μαθηματικούς στην Αρχαία Ελλάδα. Είναι φανερή η επίδραση των Μαθηματικών που είχαν αναπτυχθεί από τους Φοίνικες και τους Αιγυπτίους προς τους Έλληνες.

Οι πρώτοι Έλληνες σοφοί που ασχολήθηκαν με τα Μαθηματικά ήταν ο Θαλής ο Μιλήσιος (640-546 π.χ.) και ο Πυθαγόρας ο Σάμιος (580-490 π.χ.) που ίδρυσαν αντίστοιχα την Ιωνική και την Πυθαγορική σχολή. Είναι γνωστά πολλά γεωμετρικά θεωρήματα του Θαλή του Μιλήσιου: α) οι παρά τη βάση ισοσκελούς τριγώνου είναι ίσες. β) οι κατακόρυφες γωνίες είναι ίσες. γ) τρίγωνο ορίζεται αν δοθεί μία πλευρά και οι προσκείμενες γωνίες. δ)οι πλευρές ισογώνιου τριγώνου είναι ανάλογες . ε) κάθε διάμετρος κύκλου χωρίζει αυτόν σε δύο ίσα μέρη. στ) σε ημικύκλιο η εγγεγραμμένη γωνία είναι ορθή. Ακόμα ο Θαλής ο Μιλήσιος γνώριζε την σφαιρικότητα της γης, προέβλεπε τις εκλείψεις και χώριζε το έτος σε 365 ημέρες.

Διάδοχοι του Θαλή του Μιλήσιου στην Ιωνική σχολή ήταν ο Αναξίμανδρος, ο Αναξιμένης και ο Αναξαγόρας ο Κλαζομένιος.

Ο Πυθαγόρας ίδρυσε τη σχολή του στον Κρότωνα της Κάτω Ιταλίας στην οποία ζούσαν οι μαθητές του και κρατούσαν μυστικότητα γι αυτά που μαθαίνανε. Σύμφωνα με τον Πρόκλο αποδίδονται στον Πυθαγόρα οι εξής γεωμετρικές ανακαλύψεις: α) το άθροισμα των γωνιών κάθε τριγώνου ισούται με δύο ορθές γωνίες. β) σε κάθε ορθογώνιο τρίγωνο το τετράγωνο της υποτείνουσας ισούται με το άθροισμα των τετραγώνων των δύο άλλων πλευρών (Πυθαγόρειο θεώρημα) γ) Η κατασκευή κανονικών πολυέδρων (κοσμικών σωμάτων) κύβου, τετραέδρου, δωδεκαέδρου. δ) ο χωρισμός του επιπέδου σε κανονικά τρίγωνα, τετράγωνα ή εξάγωνα ανά 6, 4 ή 3 έχουν κοινή κορυφή. Θεωρούσαν σαν τελειότερο γεωμετρικό σχήμα τον κύκλο και τελειότερο σχήμα τη σφαίρα. Τους αριθμούς τους χώριζαν σε άρτιους και περιττούς. Το άθροισμα των περιττών αριθμών είναι 1+3+5+…….+(2ν+1)=(ν+1)2 Το γινόμενο δύο αριθμών αποτελεί επίπεδο και τριών αριθμών στέρεο σχήμα (δηλαδή κύβο αν τρεις αριθμοί είναι ίσοι).

Ο σημαντικότερος Πυθαγόρειος μετά τον θάνατο του Πυθαγόρα ήταν ο Αρχύτας ο Ταραντίνος. Η πιο σημαντική από τις άλλες σχολές ήταν η Ελεατική σχολή με τον Παρμενίδη και τον μαθητή του Ζήνωνα.

Στην Θράκη εμφανίζεται η Ατομική σχολή με τον Δημόκριτο (460-370 π.χ.) Πρώτος ανακάλυψε την οδό που οδηγεί προς το απειροστικό λογισμό, όπως αναφέρει ο Πλούταρχος και ότι εξέταζε ανά δύο γειτονικά επίπεδα τομών της σφαίρας αν είναι ίσα ή άνισα και συμπέρανε ότι αν είναι ίσα η σφαίρα είναι κύλινδρος αν είναι άνισα δαντελωτή. Γνώριζε να βρίσκει τον όγκο πυραμίδας και κώνου με γεωμετρική μέθοδο.

Προς το τέλος του 5ου π.χ. αι. η Αθήνα γίνεται το κέντρο των μαθηματικών σπουδών. Μαζί με τη σχολή της Κνίδου με τον Εύδοξο, Μέναιχμο και Αριστέα αναπτύσσεται η σχολή των Αθηνών με τον Ιπποκράτη τον Χίο, συνεχίζεται με τον Πλάτωνα και τον Θεαίτητο. Αυτές οι δύο σχολές ασχολήθηκαν με τα εξής προβλήματα : α) διπλασιασμός του κύβου β) τριχοτομήσεως της γωνίας γ) τετραγωνισμού του κύκλου.

Ο Ιπποκράτης ο Χίος (γεννηθείς το 470 π.χ.) ήταν από τους σημαντικότερους μαθηματικούς της αρχαιότητας. Γνώριζε τη φιλοσοφία του Πυθαγόρα και αναφέρεται σαν ιδρυτής της γεωμετρίας του κύκλου, ενώ οι ανακαλύψεις του σχετίζονται με τον τετραγωνισμού του κύκλου και την τριχοτόμηση της γωνίας.

Ο μεγάλος φιλόσοφος της σχολής των Αθηνών, ο Πλάτων, έβαλε τάξη στα γεωμετρικά θεωρήματα έτσι ώστε να καθοριστούν ορισμοί, αιτήματα και αξιώματα. Ο Εύδοξος (408-355 π.Χ.) μαθητής του Αρχύτα και του Πλάτωνα, ίδρυσε τη σχολή της Κυζίκου και θεωρείται ο πρώτος επιστήμονας και πατέρας της επιστημονικής αστρονομικής παρατήρησης. Ο Αριστεύς έγραψε το βιβλίο των πέντε κανονικών στερεών ( πυραμίδας, κύβου, οκτάεδρο, δωδεκάεδρο, εικοσάεδρο. Ο Θεαίτητος μαζί με τον Πυθαγόρα και τον Εύδοξο αποτελούν την τριάδα πάνω στους οποίους στηρίχθηκε ο Ευκλείδης. Ο Ευκλείδης, ο Αρχιμήδης και ο Απολλώνιος είναι οι τρεις σημαντικότεροι Μαθηματικοί της Αλεξάνδρειας. Ο Ευκλείδης (3ος π.Χ αιώνα) ανέλαβε την διεύθυνση της σχολής και έγραψε ένα πολύ σημαντικό έργο ” Τα στοιχεία ” που αποτελείται Από 13 βιβλία και χρησιμοποίησε σαν πηγές τον Πυθαγόρα τον Εύδοξο και τον Θεαίτητο. Αλλά έργα του είναι τα “Δεδομένα”, “περί διαιρέσεων”, “τα οπτικά ” και “τα κατοπτρικά” και τα “φαινόμενα”.

Ο Αρχιμήδης (287-212 π.χ.) γεννήθηκε και πέθανε στις Συρακούσες και ασχολήθηκε με όλα τα μεγάλα μαθηματικά προβλήματα της εποχής του, ενώ έκανε πλήθος εφευρέσεων που βοήθησαν πρακτικά την πόλη του. Θεωρείται πατέρας της μηχανικής και έδωσε γνώσεις κατανοητές και εφαρμόσιμες από όλους τους ανθρώπους. Έργα του είναι τα ” γεωμετρικά “, τα βιβλία περί ισορροπίας επιπέδων και στερεών σωμάτων για αριθμητική.

Απολλώνιος ο Περγαίος (3ος π.χ. αιώνας) μεγάλος γεωμέτρης με πιο γνωστό έργο του το “περί κωνικών τομών”. Έγραψε τα ” Επίπεδοι τόποι”, “περί ασύμμετρων”.

Ήρων ο Αλεξανδρεύς. Τα σπουδαιότερα έργα του είναι τα “Αυτόματα” και τα “πνευματικά”.

Ο Πτολεμαίος (150μ.Χ). Η “Μέγιστη σύνταξη” θεωρείται το καλύτερό έργο μέχρι την εποχή του Κοπέρνικου και του Κέπλερ.

Πάππος (3ος μ.Χ αιώνας) Έργο του η Συναγωγή.

Διοφάντης (4ος μ.Χ. αιώνα) Έργο του τα ” Αριθμητικά ” που από τα 13 βιβλία σώζονται μόνο τα 6 και τα ” πορίσματα “.

Ιάμβλιχος (350 μ.Χ)

Ο Θέων ο Αλεξανδρεύς (370μ.μχ.) και η κόρη του η Υπατία που ήταν η τελευταία αντιπρόσωπος της Αλεξάνδρειας.

O μουσικός… Πυθαγόρας

 

Βιογραφικά στοιχεία.
Γιος του Μνήσαρχου και της Πυθαίδας. Γεννήθηκε το 572 π.Χ. στη Σάμο και πέθανε το 490 π.Χ. στην Κάτω Ιταλία. Έζησε 22 χρόνια στην Αίγυπτο. Όταν ο βασιλιάς Καμβύσης την κατέλαβε, τον εξόρισε στη Βαβυλώνα, όπου συναναστράφηκε με Πέρσες μάγους. Δώδεκα χρόνια αργότερα αποφυλακίζεται και πηγαίνει στην Ινδία. Επιστρέφει στη Σάμο σε ηλικία 56 ετών. Αργότερα μετακινήθηκε στον Κρότωνα της Κάτω Ιταλίας, όπου ίδρυσε τη Σχολή του. σχετικά με το θάνατό του, κατά μία άποψη πέθανε εξόριστος στο Μεταπόντιο, κατ’ άλλη όμως σκοτώθηκε σε μια επιδρομή των δημοκρατικών κατά της σχολής με αρχηγό τον Κόνωνα.

Η ζωή και η δράση του.
Έλληνας μαθηματικός, θεωρητικός της Μουσικής, φιλόσοφος ηγέτης αρχαίου θρησκευτικού και πολιτικού κινήματος και ιδρυτής της Πυθαγόρειας Σχολής. Γιός του Γιος του Μνήσαρχου και της Πυθαίδας. Γεννήθηκε το 572 π.Χ. στη Σάμο και πέθανε περίπου το 490 π.Χ. στον Κρότωνα της Κ. Ιταλίας.

Σύμφωνα με την παράδοση ο Πυθαγόρας πραγματοποίησε πολλά ταξίδια στην Αίγυπτο, όπου έζησε για 22 ολόκληρα χρόνια. Εκεί έμαθε την Αιγυπτιακή γλώσσα και μελέτησε τα Ιερά Βιβλία των Αιγυπτίων. Όταν όμως ο βασιλιάς Καμβύσης την κατέλαβε, εξόρισε τον Πυθαγόρα στην Περσία, και πιο συγκεκριμένα στη Βαβυλώνα.

Εκεί συναναστράφηκε με Πέρσες μάγους, με αποτέλεσμα να εμπλουτίσει τις γνώσεις του με τις μαθηματικές και αστρονομικές δοξασίες των Ασσυρο-Βαβυλωνίων.

Ύστερα από δώδεκα χρόνια ελευθερώνεται και πηγαίνει στην Ινδία, όπου μυείται στα τελετουργικά των Βραχμάνων. Μάλιστα είναι και ο πρώτος μη Βραχμάνος που γίνεται αποδεκτός. Έτσι παίρνει το όνομα «Γιαβαντσάρια» ή «Γιουναντσάρια», που σημαίνει Ίωνας δάσκαλος.

Αργότερα αποφασίζει να επιστρέψει στην Ελλάδα. Αρχικά επισκέπτεται τη Λέσβο, όπου υπήρξε μαθητής του Φερεκύδη και έπειτα τη Μίλητο, όπου γίνεται μαθητής του Αναξίμανδρου και του Θαλή.

Τέλος επιστρέφει στα πάτρια εδάφη, δηλαδή στη Σάμο, σε ηλικία 56 ετών με σκοπό να δημιουργήσει μία Φιλοσοφική Σχολή. Η Σάμος όμως εκείνη την εποχή βρισκόταν υπό την εξουσία του τυράννου Πολυκράτη, του οποίου ο Πυθαγόρας ήταν αντίπαλος. Ο λόγος για τον οποίο συνέβη αυτό δεν είναι απολύτως ξεκάθαρος. Υπάρχει από τη μία η άποψη που υποστηρίζει πως ο Πολυκράτης ένιωθε αντιπάθεια για τους περιπλανώμενους φιλοσόφους και για αυτό το λόγο δεν επέτρεψε στον Πυθαγόρα να δημιουργήσει τη Σχολή του. Από την άλλη όμως υπάρχει η άποψη που υποστηρίζει πως ο Πυθαγόρας ανήκε στην αριστοκρατική τάξη, η οποία εναντιώθηκε στην Τυραννίδα του Πολυκράτη.

Είτε για τον ένα, είτε για τον άλλο λόγο, ένα είναι το σίγουρο, ότι δηλαδή ο Πυθαγόρας εξαιτίας αυτών των αντιθέσεων αναγκάστηκε να εκπατριστεί. Αρχικά πήγε στη Σικελία, μετά στη Σύβαρη και στον Τάραντα, μέχρι που άκουσε κάποιες θαυμαστές ιστορίες για τον Κρότωνα στην Κ. Ιταλία, για πρωτοποριακές ιδέες, τέχνες, ευτυχισμένους πολίτες, και αποφάσισε πως όλα έδειχναν ότι σε εκείνη την ανθούσα αποικία θα μπορούσε να ιδρύσει τη Σχολή του. Έτσι μετανάστευσε οριστικά στον Κρότωνα, όπου και ίδρυσε τη Σχολή του.

Εκεί έγινε ευπρόσδεκτος και επιβλήθηκε ως επιστημονική αυθεντία (μάλιστα σύμφωνα με μαρτυρίες πολλοί τον θεωρούσαν ως γιο του Απόλλωνα ή του Ερμή). Η Σχολή που ίδρυσε, είχε τη μορφή ηθικοθρησκευτικής, επιστημονικής και πολιτικής κοινότητας («εταιρείας»), τα μέλη της οποίας έπαιξαν σημαντικό ρόλο στα πολιτικά δρώμενα της Ιταλίας. Όμως τα «πιστεύω» των Πυθαγορείων προκάλεσαν τις βίαιες αντιδράσεις των πολιτικών τους αντιπάλων με αποτέλεσμα να φτάσουν στο σημείο άλλους να τους φονεύσουν και άλλους να τους διώξουν.

Όσον αφορά το θάνατο του Πυθαγόρα υπάρχουν δύο απόψεις. Σύμφωνα με την πρώτη σκοτώθηκε σε μια από τις επιδρομές των δημοκρατικών κατά της Σχολής με αρχηγό τον Κόνωνα, και σύμφωνα με τη δεύτερη, ύστερα από όσα συνέβαιναν, αναγκάστηκε να καταφύγει στο Μεταπόντιο, όπου λίγο αργότερα πέθανε.

Πυθαγορισμός

Βασικά ενδιαφέροντα του Πυθαγόρα και η διδασκαλία του.
Όπως γίνεται παραπάνω φανερό η ζωή και ο θάνατος του Πυθαγόρα περιβάλλονται από μύθους και θρύλους. Το ίδιο συμβαίνει και με τη διδασκαλία του. Η φιλοσοφία που ακολουθούσε ήταν ιδιόρρυθμη και καλυπτόταν από ένα μανδύα μυστικισμού. Αυτό δημιουργούσε στους νέους την περιέργεια από τη μία και το ενδιαφέρον από την άλλη για την εκμάθηση της διδασκαλίας του, με αποτέλεσμα όλο και περισσότεροι νέοι να μυούνται, παρόλο που τους ανάγκαζε να ζουν με αυστηρή πειθαρχία.

Επειδή η επίδρασή του ήταν τόσο μεγάλη, γρήγορα οδηγήθηκε στο δικαστήριο με τις κατηγορίες της διαφθοράς των νέων και της αθεΐας. Όμως οι κατηγορίες δεν έγιναν αποδεκτές και τελικά αθωώθηκε.

Θρησκεία και ηθική.
Η Σχολή του κατά την παράδοση φαίνεται πως υπήρξε αρχικά ένας θρησκευτικός όμιλος με επίκεντρο τον Πυθαγόρα και τη λατρεία του Απόλλωνα και των Μουσών, παλαιών θεοτήτων που τις θεωρούσαν ως προστάτιδες της ποίησης και της πνευματικής καλλιέργειας.

Από θρησκευτική άποψη, η θεωρία του Πυθαγόρα έχει σχέση με τη θεωρία των Ορφικών. (Ο Ορφισμός πρέσβευε ότι μέσω της έκστασης μπορούσε να επιτευχθεί η πνευματική ενόραση στη θεϊκή καταγωγή και τη φύση της ψυχής). Ενώ όμως στον Ορφισμό η κάθαρση του αμαρτωλού γίνεται με τις ορφικές τελετές, στον Πυθαγορισμό γίνεται με τη μελέτη των επιστημών, κυρίως των Μαθηματικών και της Μουσικής.

Ο Πυθαγόρας ήταν υποστηρικτής της Μετεμψύχωσης. Πίστευε, δηλαδή, ότι μετά το θάνατο η ψυχή του ανθρώπου αν είναι «τέλεια», μεταβαίνει και ενώνεται με το Θεό, ενώ αν ο άνθρωπος έχει διαπράξει αμαρτήματα κατά τη διάρκεια της ζωής του, επιστρέφει με τη μορφή φυτού ή ζώου, για τιμωρία και εξαγνισμό. Μάλιστα δίδασκε πως όλα τα φυτά και τα ζώα που βλέπουμε γύρω μας δεν είναι παρά άνθρωποι αμαρτωλοί, που έχουν σταλεί εδώ σε αυτή τη μορφή- από ένα αόρατο και ακατανόητο σύμπαν- για να «εξαγνιστούν».

Η θεωρία της Μετεμψύχωσης φαίνεται πως έκανε τον Πυθαγόρα να διεκδικεί μια ημιθεϊκή υπόσταση, σε στενή σχέση με το θεό Απόλλωνα. Πίστευε δηλαδή ότι μπορούσε να θυμάται τις προηγούμενες μετενσαρκώσεις του, με αποτέλεσμα να θεωρεί τον εαυτό του ανώτερο από τους υπόλοιπους ανθρώπους, δηλαδή με περισσότερες εμπειρίες και γνώσεις.

Οι κανόνες της θρησκευτικής ζωής που δίδασκε ο Πυθαγόρας ήταν κατά βάση τελετουργικοί: αποφυγή της συζήτησης γύρω από ιερά θέματα, λευκή μόνον ενδυμασία, αποχή από ορισμένα είδη καρπών, όπως τα κουκιά, και φυσικά τήρηση σεξουαλικής αγνότητας.

Επίσης υπάρχουν ενδείξεις ότι δίδασκε την κάθαρση της ψυχής μέσω της μουσικής και της φιλοσοφίας, προκειμένου να φτάσει κανείς σε Μετενσαρκώσεις ανωτέρου επιπέδου. Η «ομοίωση προς το Δάσκαλο» και έτσι η «προσέγγιση προς τους θεούς» ήταν η πρόκληση που επέβαλε σε όλους τους μαθητές του. Η σωτηρία, και για μερικούς ίσως η τελική ένωση με το θεϊκό κόσμο μέσω της σπουδής της κοσμικής τάξης, έγινε μία από τις κύριες αντιλήψεις στη Σχολή του.

Σήμερα ο Πυθαγόρας, εξαιτίας των αντιλήψεών του περί θρησκείας και ηθικής, θεωρείται ένας από τους μεγάλους παιδαγωγούς της αρχαίας Ελλάδας. Αυτός ήταν, άλλωστε, που δίδαξε πρώτος την εσωτερική αφοσίωση, τη μετριοφροσύνη, την ευσέβεια, την εμπιστοσύνη και τη «σωματική» αγνότητα.

Μεταφυσική και θεωρία των αριθμών.
Η θεωρία των αριθμών είναι το πιο χαρακτηριστικό στοιχείο του Πυθαγορισμού. Τα αντικείμενα «είναι» αριθμοί ή «ομοιάζουν» με αριθμούς.

Ο Πυθαγόρας «συνέλαβε» τους αριθμούς κατά την προσπάθειά του να βρει μια πρωταρχική, άϋλη, αναλλοίωτη αρχή των όντων. Οι αριθμοί είναι αυτοί λοιπόν που αποτελούν την πρώτη αρχή, την προσδιοριστική δύναμη του κόσμου και στη σχέση ανάμεσά τους βρίσκεται η ουσία των όντων. Για το λόγω του ότι είναι αυτή η ίδια η ουσία του κόσμου και όχι απλώς σύμβολα ποσοτικών σχέσεων, οι αριθμοί θεωρούνται «ιεροί». Ακόμη και οι αφηρημένες έννοιες στον Πυθαγορισμό συνδέονται με τους αριθμούς. Π.χ. η δικαιοσύνη συνδέεται με τον αριθμό 4 δηλαδή με τον πρώτο τετραγωνικό αριθμό και ο γάμος με τον αριθμό 5. Ο άνθρωπος παριστάνεται με τον αριθμό 250 κ.λ.π. Οι ψυχολογικοί συνειρμοί που λειτούργησαν εδώ δεν έχουν αποσαφηνιστεί.

Κοσμική Αρμονία: στον Πυθαγορισμό κοσμική σημασία έχει η «ιερή δεκάδα»: η μυστική της ονομασία, τετρακτύς της δεκάδας, συνεπάγεται ότι 1+2+3+4=10, αλλά μπορεί να νοηθεί και ως το «τέλειο τρίγωνο».

Όπως είπαμε η ουσία των όντων σύμφωνα με τον Πυθαγόρα είναι οι αριθμοί. Επιπλέον πίστευε ότι το σύμπαν προήλθε από το χάος και απέκτησε μορφή με το μέτρο και την αρμονία, γι’ αυτό και πρώτος το ονόμασε «Κόσμο», δηλαδή τάξη και αρμονία.

Αρμονία όμως για το σώμα είναι η ψυχή, η οποία διατηρεί κάποια συμμετρία ανάμεσα στο υλικό και το πνευματικό στοιχείο του ανθρώπου. Η ψυχή έχει τις ιδιότητες της ταυτότητας, της ετερότητας, της στάσης και της κίνησης. Αυτή είναι η «τετρακτύς» για την ψυχή. Αυτές οι φιλοσοφικές του αντιλήψεις επηρέασαν τον Πλάτωνα, ο οποίος αργότερα θεωρεί ότι η αρμονία της μουσικής καθρεφτίζει την αρμονία της ψυχής.

Σύμφωνα με τον Πυθαγόρα το σύμπαν βρίσκεται σε διάταξη αρμονίας και η θεωρία του, η θέασή του, είναι αυτή που φέρνει την κάθαρση. Αυτό οδήγησε στη θεωρία του Πυθαγόρα για την «Αρμονία των σφαιρών». Το σύνολο των ήχων, δηλαδή, που παράγονται από την περιστροφή των πλανητών, ανάλογα πάντα με την απόστασή τους από τη γη, και οι οποίοι ,όμως, δεν ακούγονται.

Αριθμητική και Γεωμετρία.
Στην αριθμητική η συμβολή του Πυθαγόρα δεν ήταν τόσο σημαντική όσο η συμβολή του στην επιστήμη της Γεωμετρίας.

Παρόλα αυτά ο Πυθαγόρας είναι αυτός που δημιούργησε τον Πυθαγόρειο Πίνακα ή Άβακα, τον πασίγνωστο σε όλους μας πίνακα πολλαπλασιασμού ή αλλιώς προπαίδεια. Είναι δηλαδή ο πίνακας που δίνει τα γινόμενα των δέκα πρώτων ακέραιων αριθμών.

Στη Γεωμετρία η συμβολή του είναι αξιοσημείωτη αφού είναι αυτός που ανακάλυψε ότι το τετράγωνο της υποτείνουσας ενός ορθογωνίου τριγώνου ισούται με το άθροισμα των τετραγώνων των καθέτων πλευρών. Αυτή η θεωρία του σήμερα ονομάζεται στην επιστήμη της γεωμετρίας «πυθαγόρειο θεώρημα».

Μουσική

Διάστημα.
Η σχέση μεταξύ δύο αριθμών, αυτό δηλαδή που ονομάζεται σήμερα στην αριθμητική και στη γεωμετρία λόγος, στη μαθηματική θεωρία της Μουσικής του Πυθαγόρα ονομάζεται «Διάστημα».

Στη θεωρία της Μουσικής μάλιστα η λέξη διάστημα είχε διπλή σημασία. Διότι αφενός μεν ονομαζόταν διάστημα η αριθμητική σχέση με την οποία εκφραζόταν ο λόγος του μουσικού διαστήματος, αφετέρου δε αυτή η λέξη ήταν σύμφωνη με την καθημερινή έννοιά της και το «τμήμα ευθείας», δηλαδή την απόσταση μεταξύ δύο σημείων.

Το μουσικό διάστημα, που εκφραζόταν ως «σχέση δύο αριθμών προς αλλήλους» στη θεωρία της Μουσικής του Πυθαγόρα ονομαζόταν αρχικά διάστημα = απόσταση δυο σημείων απ’ αλλήλων. Το «διάστημα» αυτό είχε πράγματι δύο συνοριακά σημεία (πέρατα, όρους), τα οποία δινόντουσαν ως αριθμοί.

Οι αρχαίοι θεωρητικοί ενδιαφέρονταν κυρίως για τα σύμφωνα διαστήματα ή συμφωνίες. Το όνομα ενός τέτοιου διαστήματος στην Πρακτική της Μουσικής ήταν συνήθως «συμφωνία», αφού άλλωστε για αυτό το λόγο ήθελαν να εκφράσουν το «συγχρονισμένο τονισμό», το «συμφωνείν» δηλαδή δύο ήχων. Ο Πυθαγόρας κυρίως ασχολήθηκε με το «Οκτάτονο (δια πασών, Oktave)», με το «Τετράτονο (δια τεσσάρων, Quarte)» και με το «Πεντάτονο (δια πέντε, Quinte)».

Υπολογισμός διαστημάτων.
Πιο συγκεκριμένα ο Πυθαγόρας ήταν αυτός που πρώτος έθεσε τις βάσεις της επιστήμης της Μουσικής με μια επιστημονικά θεμελιωμένη θεωρία της Μουσικής. Ανακάλυψε τη σχέση ανάμεσα στο μήκος των χορδών και το τονικό ύψος που δίνουν.

Για να το πετύχει αυτό χρησιμοποίησε ένα έγχορδο όργανο, που το δημιούργησε ο ίδιος, το «Μονόχορδο».

Αρχικά υπολόγισε ότι δύο χορδές, που η μία είναι διπλάσια από την άλλη (άρα έχουν σχέση 2/1), παράγουν ήχους, δηλαδή νότες, που απέχουν διάστημα Οκτάβας ή «δια πασών». Στη συνέχεια διαπίστωσε ότι όταν δύο χορδές έχουν σχέση 3/2 τότε το διάστημα που σχηματίζουν οι νότες που παράγονται είναι μια 5η Καθαρή. Με αυτά τα διαστήματα, γνωρίζοντας κανείς ότι όταν προσθέτουμε διαστήματα πολλαπλασιάζουμε τους λόγους τους και αντίθετα όταν αφαιρούμε, τους διαιρούμε, -γιατί δεν πρόκειται για ποσότητες αλλά για αναλογίες- μπορούμε να υπολογίσουμε τους λόγους όλων των διαστημάτων. [Π.χ. με αφετηρία τη νότα ντο, η νότα σολ είναι 5η Καθαρή πάνω, άρα έχει σχέση 3/2. Το ρε, και πάλι, είναι μια 5η Καθαρή πάνω από το σολ, άρα σε σχέση με το ντο είναι (3/2)2 = 9/4.

9/4 όμως είναι η σχέση του διαστήματος 9ης. Για να βρούμε λοιπόν το διάστημα 2ας θα πρέπει να διαιρέσουμε (9/4) : (2/1) = 9/8. Άρα η 2η Μεγάλη δίνεται από τη σχέση 9/8.]

Με αυτό τον τρόπο ο Πυθαγόρας υπολόγισε όλα τα διαστήματα και απέδειξε ότι υπάρχουν δύο ειδών ημιτόνια: τα διατονικά (μι-φα και σι-ντο) και τα χρωματικά (π.χ. φα-φα#). Το διατονικό το ονόμασε λείμμα και το χρωματικό αποτομή. Τη διαφορά τους την ονόμασε Πυθαγόρειο Κόμμα, το οποίο μάλιστα είναι ίσο προς τη διαφορά (3/2)12 και (2/1)7. Κανονικά 12 πέμπτες πρέπει να ισούνται με 7 οκτάβες (στο πιάνο αυτά τα διαστήματα ταυτίζονται). Ωστόσο ο Πυθαγόρας απέδειξε πως διαφέρουν κατά το Πυθαγόρειο Κόμμα.

Βέβαια από την αρχαιότητα είχε παρατηρηθεί ότι αυτή η διαδικασία δεν κλείνει ποτέ με την αφετηρία της όσο και αν πολλαπλασιάζουμε, παρόλα αυτά η απόσταση μικραίνει χωρίς ποτέ να γίνεται 0.

Το πλεονέκτημα του Πυθαγόρειου υπολογισμού των διαστημάτων είναι το ότι αποτελεί έναν τρόπο που να στηρίζεται σε αριθμητικές πράξεις και όχι στο αυτό ή την εμπειρία. Αντίθετα το μειονέκτημά του είναι πως σήμερα δεν μπορεί να εφαρμοστεί για το χόρδισμα των οργάνων.

Το Πυθαγόρειο Κόμμα είναι αυτό που οδήγησε στον Ισοτονικό Συγκερασμό (η διαίρεση της οκτάβας σε δώδεκα ίσα τμήματα-ημιτόνια). Μ’ αυτόν τον τρόπο τα φυσικά διαστήματα τροποποιούνται ελαφρά ώστε όλα τα ημιτόνια να είναι ίδια και οι δώδεκα 5ες να συμπίπτουν με επτά 8άβες (δηλαδή 12 5ες = 7 8άβες).

Ο Πυθαγόρας έκανε τους υπολογισμούς του χωρίς να κάνει συγκεκριμένη αναφορά σε κάποιο μουσικό όργανο ή σε κάποια τονικότητα.

Μέχρι το 16ο αι. ο Πυθαγόρειος υπολογισμός των διαστημάτων υπήρξε ο πυρήνας της τεχνικής χορδίσματος των οργάνων.

Διαφορές με τον Αριστόξενο τον Ταραντίνο.
Ο Αριστόξενος ο Ταραντίνος, νεότερος του Πυθαγόρα (περί το 375), υπήρξε φιλόσοφος και σημαντικότατος θεωρητικός της Μουσικής. Γι’ αυτό το λόγο μάλιστα, στην αρχαιότητα, του δόθηκε η ονομασία «ο Μουσικός».

Σύμφωνα με τον Αριστόξενο διάστημα είναι το περιεχόμενο τμήμα μεταξύ δύο φθόγγων, που έχουν την ίδια ένταση (ύψος). Ως προς αυτόν λοιπόν το βασικό όρο, το διάστημα παρουσιάζεται ως μία διαφορά εντάσεως και ως χώρος, αυτός μπορεί να περιέχει τόνους (φθόγγους) οξύτερους από τους βαρύτερους και βαρύτερους από τους οξύτερους και των οποίων η ένταση το διάστημα αυτό (τύπος δεκτικός φθόγγων). Η διαφορά όμως των υψών αυτών των φθόγγων δείχνει κατά πόσο η ένταση είναι περισσότερη ή λιγότερη.

Ο W. Burkert ανέφερε την εξής πρόταση για τον Αριστόξενο και τους Πυθαγορείους:

«Η έννοια του ευθύγραμμου τμήματος είναι συνδεδεμένη με το όνομα του Αριστόξενου, η δε διδασκαλία περί της αναλογίας της Μουσικής όμως είναι συνδεδεμένη με τους Πυθαγορείους…».

ως γνωστό ο Αριστόξενος ήταν μεγάλος αντίπαλος της Πυθαγόρειας θεωρίας. Θα παρουσιάσω τη διδασκαλία του συνοπτικά, σύμφωνα με τον C.V.Jan:

«Στην Αρμονική του δεν ερευνά πως δημιουργείται ο κάθε φθόγγος, αν είναι αριθμός ή ταχύτητα (ρυθμός). Το «ούς» πρέπει μόνο αδεσμεύτως σε ότι αφορά τους τόνους να «θεάται» το βασίλειο των φθόγγων. Αυτό μόνο είναι ικανό να μας πληροφορήσει με βεβαιότητα, ποιοι φθόγγοι βρίσκονται σε αρμονική σχέση μεταξύ τους… Το σύστημα της διδασκαλίας του βασίζεται πάνω στις εύκολες αντιληπτές συγχορδίες της τετρατόνου και της πεντατόνου, και χωρίς να ερευνήσει ποια αριθμητική σχέση βρίσκεται στη βάση τους, καθορίζει συμφώνως προς αυτές τον ολόκληρο και τον μισό τόνο κ.λ.π.».

Δηλαδή θέλει να μας εξηγήσει ότι το σύστημα της διδασκαλίας του δεν στηρίζεται στις αριθμητικές σχέσεις, όπως του Πυθαγόρα, αλλά βασίζεται στην ικανότητα του αυτιού να αντιλαμβάνεται την αρμονική σχέση των μουσικών τόνων. Μπορεί να μην ερευνά τις αριθμητικές σχέσεις μέσα στην οκτάβα, καθορίζει όμως τον ολόκληρο και τον μισό τόνο και κατασκευάζει μια κλίμακα με βάση το ένα δωδέκατο του τόνου. Επομένως η μέθοδός του ήταν, καθαρά, εμπειρική.

Πυθαγόρειοι
Μαθητές του Πυθαγόρα, οπαδοί της φιλοσοφικής του θεωρίας, μέλη της ιδιότυπης φιλοσοφικής του Σχολής ή εταιρίας. Για τη δράση τους είναι λίγα πράγματα γνωστά σήμερα σε σχέση με όσα γνωρίζουμε για τον ίδιο τον Πυθαγόρα. Λέγεται ότι η ασάφεια αυτή οφείλεται στο ότι οι επιμέρους απόψεις τους αποδίδονταν στον Πυθαγόρα ή οφείλονταν στην έμπνευση αυτού. Αυτό βέβαια συνέβη μέχρι την εποχή του Πλάτωνα και του Αριστοτέλη.

Εξάλλου οι Πυθαγόρειοι έδιναν όρκο ότι θα τηρούσαν απόλυτη σιωπή σ’ ότι αφορά την Πυθαγόρεια Διδασκαλία και η κοινολόγηση των απόψεών τους απαγορευόταν. Όσα είναι γνωστά για αυτούς, τα γνωρίζουμε κυρίως από τον Πλάτωνα και τον Αριστοτέλη.

Σύμφωνα με τις αναφορές του Διογένη του Λαέρτιου, ο αριθμός των μαθητών έφτανε τους τριακόσιους, από τους οποίους αρκετοί σκοτώθηκαν από την εξέγερση των Κροτωνιατών και οι υπόλοιποι διέφυγαν.

Από τη στιγμή που διέφυγαν ήταν φυσικό να διασκορπιστούν. Η διασπορά οδήγησε μοιραία σε δογματικές διαφορές ανάμεσά τους και σύμφωνα με τον Αριστοτέλη από τον 5ο αι. και μετά οι Πυθαγόρειοι δε διδάσκουν πλέον τα ίδια.

Διακρίθηκαν βασικά δύο ομάδες Πυθαγορείων: οι ακουσματικοί και οι μαθηματικοί, ενώ οι Πυθαγόρειες διδαχές διακρίθηκαν σε τρεις περιόδους: οι δύο πρώτες περίοδοι περιλαμβάνουν τις διδαχές που χρονολογούνται πριν από τον Παρμενίδη και η Τρίτη έχει σχέση με τη γενιά των Πυθαγοριστών (με αρχηγό το Φιλόλαο) στα τέλη του 5ου αιώνα.

Αστρονομία.
Στην Αστρονομία, πιθανολογείται πως πρώτος ο Πυθαγόρας ήταν αυτός που θεώρησε πως η γη είναι στρογγυλή. Ακόμη ήταν αυτός που δέχτηκε πρώτος πως η γη περιφέρεται γύρω από το «Κεντρικό Πυρ» (την «Εστία του Παντός») και δημιουργείται έτσι μια περιστρεφόμενη «ουράνια σφαίρα».

Όμως οι Πυθαγόρειοι αργότερα ήταν αυτοί που έκανα γνωστή αυτή τη θεωρία και μάλιστα την ανέπτυξαν ακόμη περισσότερο. Πίστευαν δηλαδή πως γύρω από το κεντρικό πυρ δεν περιστρεφόταν μόνο η γη, αλλά περιστρέφονταν και άλλες σφαίρες: μια με όλους τους απλανείς αστέρες, ανά μία με τον Ήλιο και τη Σελήνη και ανά μια με τους τότε γνωστούς πλανήτες (Άρης, Ζευς, Κρόνος, Ερμής, Αφροδίτη). Για να συμπληρωθεί λοιπόν ο ιερός αριθμός δέκα (10), παραδέχτηκαν ότι υπάρχει και άλλο ένα ουράνιο σώμα με κυκλική κίνηση γύρω από το κοινό κέντρο, η «Αντίχθων».

Αυτό το σώμα δεν ήταν ορατό από τη Γη, γιατί δε φαινόταν από το κατοικημένο μέρος της. Ακόμη υποστήριζαν ότι οι αριθμητικοί λόγοι, από τους οποίους εξαρτάται η αρμονία στη Μουσική, θα πρέπει να συντελούν και στην αρμονική δομή του Σύμπαντος. Συνεπώς, από τις αποστάσεις μεταξύ των ουράνιων σωμάτων θα προκαλείται μια ουράνια Μουσική, την οποία όμως οι άνθρωποι δεν αντιλαμβάνονται, επειδή συνεχίζεται αδιάκοπα και αδιατάραχτα.

Επιδράσεις
Σήμερα είναι βέβαιο ότι ο Πυθαγόρας υπήρξε μεγάλη προσωπικότητα της αρχαιότητας σε πολλούς τομείς, όπως τα μαθηματικά, η αστρονομία, η μουσική…

Οι φιλοσοφικές, ηθικές και κοινωνικοπολιτικές δοξασίες του ίδιου του Πυθαγόρα, αλλά και των μαθητών του, επηρέασαν αποφασιστικά την ελληνική σκέψη και φιλοσοφία.

Τα στοιχεία που έχουμε για τον Πυθαγόρα και τη φιλοσοφική του θεωρία οφείλονται στις μαρτυρίες του Ηράκλειτου, του Ηρόδοτου, του Εμπεδοκλή, του Ξενοφάνη και του Ίωνα του Χίου. Οι μαρτυρίες αυτές αλλά και μεταγενέστερες, όπως του Αριστοτέλη και του Πλάτωνα, θεμελιώνουν την άποψη ότι ο Πυθαγόρας είναι ιστορική φυσιογνωμία.

Ενδεικτική Βιβλιογραφία
1) Γιάννου Δημ., «Ιστορία της Μουσικής (Σύντομη γενική επισκόπηση)», τόμος α΄, Θεσσαλονίκη. University Studio Press, 1994, σελ. 91-93.
2) Ulrich Michels: «Άτλας της Μουσικής». Τόμος Α΄, Αθήνα, Μουσικός Οίκος «Φίλιππος Νάκας», σελ. 175.
3) Karl Nef: «Ιστορία της Μουσικής», Δεύτερη έκδοση. Εκδόσεις «Ν. Βότσης», Αθήνα 1985, σελ. 50-51.
4) Λήμμα: «Πυθαγόρας», Επιστήμη και Ζωή, εκδοτικές και Εμπορικές Επιχειρήσεις Χατζηϊακώβου Α.Ε., τόμος 7ος, σελ. 24-26 και τόμος 16ος, σελ. 246-247.
5) Internet: www.apologitis.com/gr/ancient/filosof-dioks.htm

 

πηγή:Βάσω Κ. Ηλιάδη-ΠΕΕΜΔΕ

 

 

 ο χρυσός φ

 Στην άκρη του νήματος βρίσκονται πέντε ερωτήματα καθένα από τα οποία περιμένει την απάντησή του

 

1. Υπάρχει αριθμός τέτοιος ώστε εάν τον υψώσεις στο τετράγωνο να αυξηθεί κατά μία μονάδα; Ποιος είναι αυτός ο αριθμός;

2. Υπάρχει αριθμός τέτοιος ώστε εάν τον ελαττώσεις κατά μία μονάδα να αντιστραφεί;

Ποιος είναι αυτός ο αριθμός;

3. Χωρίζουμε ένα ευθύγραμμο τμήμα σε δύο κομμάτια. Στη γλώσσα της ελληνικής Γεωμετρίας λέμε ότι κάνουμε μια ΤΟΜΗ η οποία είναι ΧΡΥΣΗ εφόσον ο λόγος του μεγάλου προς το μικρό είναι ίσος με το λόγο ολόκληρου προς το μεγάλο. Ποια είναι η τιμή αυτού του λόγου;

4. Το κανονικό δεκάγωνο εγγεγραμμένο σε  κύκλο.  Η ακτίνα του κύκλου είναι βέβαια μεγαλύτερη από την πλευρά του.  Πόσες φορές;

5. Η ακολουθία Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025 . . Καθένας από τους όρους της προκύπτει από το άθροισμα των δύο που προηγούνται.  α_ν = α_ν-1 + α_ν-2 .

Αν φτιάξουμε μια ακολουθία με όρους τους λόγους των διαδοχικών όρων της ακολουθίας θα έχουμε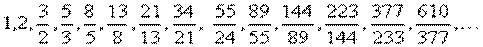    

Θα διαπιστώσουμε ότι «συγκλίνει» σε κάποιο αριθμό. Ποιος είναι αυτός ο αριθμός;

 

 «Εκείνος»  δοκίμασε ε να δώσει απαντήσεις στα τέσσερα από τα ερωτήματα. Όσο για το πέμπτο περίμενε τη δεκαετία του 1970 να ανακαλυφθεί το κομπιουτεράκι και τότε το «είδε» κάνοντας πράξεις. 

 

Δοκίμασε το πρώτο . Υπέθεσε  ότι ο ζητούμενος αριθμός είναι ο x 

                x² = x + 1            x²–x-1= 0            x = (1+Ö5) /2

 

Δοκίμασε το  δεύτερο . Υπέθεσε  ότι ο ζητούμενος αριθμός είναι ο y 

           y – 1 = 1/y                     y = (1+Ö5) /2           

 

Δοκίμασε το  τρίτο. Υπέθεσε  ότι ο ζητούμενος λόγος είναι ίσος με τον αριθμό z  

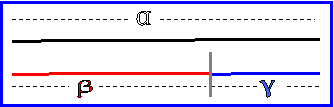z = α/β = β/γ    ή     α/β = β/(α-β)   

 ή   α(α-β) = β²   ή α² – αβ –β² = 0 ή

ή  α² – αβ –β² = 0   (α/β)²-(α/β) –1 = 0

     z²–z-1 = 0     z = (1+Ö5) /2

 

 

Δοκίμασε να απαντήσει στο  τέταρτο. Σχεδίασε το δεκάγωνο και είδε ότι κάθε ισοσκελές τρίγωνο που

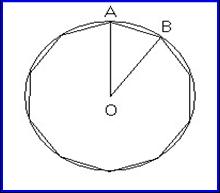δημιουργείται με μία πλευρά (L) του δεκαγώνου

και δύο ακτίνες (R) στα άκρα της είναι ισοσκελές

 με γωνία κορυφής 36⁰., οπότε οι δύο άλλες

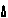 γωνίες του είναι 72⁰.  Φέρνοντας  τη διχοτόμο

της ΟΑΒ είδε η γωνία ΟΑΔ θα είναι 36⁰ και

 η ΟΔΒ = 72⁰ άρα τα τρίγωνα ΟΑΒ και ΔΑΒ θα

είναι όμοια και ισχύει ΟΑ/ΑΒ = ΑΔ/ΔΒ .

                         

Αλλά ΟΑ =R   ΟΔ=ΑΔ=ΑΒ=L και ΔΒ= R–L , οπότε   

R/ L =  L/ R–L    R²– RL–  L² = 0          R = L (1+Ö5) /2

Η ακτίνα του κύκλου είναι (1+Ö5) /2 φορές μεγαλύτερη από την πλευρά του κανονικού δεκαγώνου

 

Το πέμπτο το αντιμετώπισε με ένα κομπιουτεράκι. Υπολόγισε με το κομπιουτεράκι,  τις τιμές αυτών των λόγων, σε δεκαδικούς

 και είδε ότι    2/1 =  2                         3/2 = 1,5000000            5/3 = 1,666666

              8/5 = 1,6000000                 13/8 = 1,6250000            21/13 = 1,6153846                  

        34/21 = 1,6190476                    55/34 = 1,617647               89/55 = 1,6181818

      144/89 = 1,6179775              233/144 = 1,6180555           377/233 =1,6180257

     610/ 377 = 1,6180371                 987/610 = 1,6180327       1597/987=1,6810344      

2584/1597=1,6180338              4181/2584  = 1,6180340        6765/4181 = 1,6180339         

10946/6765 = 1,6180339    17711/10946 = 1,6180339     28657/17711 = 1,6180339     46368/28657 = 1,6180339

Διαπίστωσε  ότι από τον λόγο 6765/4181 και μετά, το κομπιουτεράκι έφθανε στα φθάνει στα  όρια του, στα δέκα δηλαδή ψηφία από τα οποία τα εννέα είναι δεκαδικά. Οι λόγοι που ακολουθούν δεν είναι μεταξύ τους ίσοι αλλά το κομπιουτεράκι αδυνατεί να το δείξει.

Του έδειχνε  συνεχώς έναν αριθμό ο οποίος συμπίπτει σε εννέα δεκαδικά ψηφία με τον αριθμό φ.

Και είναι γεγονός ότι το όριο της ακολουθίας που είχε δημιουργήσει ήταν ο φ.

 

 Το γενικό συμπέρασμα. Και στις τρεις περιπτώσεις ο ζητούμενος αριθμός

    είναι ίσος με  (1+Ö5) /2 ή  με επτά δεκαδικά ψηφία  ίσος με

                   1, 6180339. . . 

   ο αριθμός αυτός διεθνώς συμβολίζεται με το ελληνικό γράμμα φ

                  Είναι ο λεγόμενος  ΧΡΥΣΟΣ ΑΡΙΘΜΟΣ ή ΧΡΥΣΗ ΤΟΜΗ.

 

 

 

Ο Leonardo da Vinci μας έμαθε ότι εάν το ύψος οποιουδήποτε ανθρώπου διαιρεθεί με το ύψος στο οποίο βρίσκεται ο αφαλός του το αποτέλεσμα θα είναι ίσο με φ.

1700 χρόνια νωρίτερα είχε ασχοληθεί μαζί του ο Ευκλείδης αλλά τα  βιβλία που αναφέρονται σε αυτόν δεν είναι κυρίως βιβλία μαθηματικών. Είναι βιβλία διαπνεόμενα από  μυστικισμό και μας μιλούν για το σουξέ που είχε ο φ διατηρούμενος σαν λείψανο από τους αρχαίος μύστες, μας λένε πως ο φ είναι ένα μυστικό της ομορφιάς το οποίο διατηρήθηκε και πως δεν είναι τυχαίο ότι η πρόσοψη του Παρθενώνα εγγράφεται σε ένα χρυσό ορθογώνιο με πλευρές που έχουν λόγο φ.

Στην ευρωπαϊκή παράδοση ο όρος «χρυσή τομή» κάνει την εμφάνισή του στο έργο του Leorardo da Vinci σε γλώσσα λατινική ως sectio aurea.

Η χρυσή του συμβόλου «φ» εμφανίζεται πολύ αργότερα ύστερα από πρόταση του αμερικανού μαθηματικού  Mark Barr. Το πρότεινε ως αρχικό του ονόματος του γλύπτη Φειδία ο οποίος χρησιμοποίησε τη χρυσή τομή στα σχέδια των έργων  του.

 

 

ο φ και η Άλγεβρα.

Ο φ είναι η θετική ρίζα της εξίσωσης φ² – φ -1 = 0 .

Ισχύει συνεπώς φ² = 1+φ και φ = Ö(1+φ)

.

Η σχέση μπορεί να χρησιμοποιηθεί και για την οικοδόμηση ενός άλλου ορισμού του φ.

         φ = Ö{1+Ö(1+φ)}       ή φ = Ö{1+Ö(1+Ö1+φ )}

Αυτό μπορεί να συνεχίζεται επ’ άπειρον

 

Για τον φ ισχύει επίσης: φ=1 +1/φ    φ=1+1/(1+1/φ)

Για τον φ ισχύει ακόμα:

φ = φ,               φ² = φ + 1        φ³ = 2φ + 1,

φ⁴ = 3φ + 2     φ⁵ = 5φ + 3,       φ⁶ = 8φ + 5, . . .

 

ο φ και η Γεωμετρία

Με κανόνα και διαβήτη

Η χρυσή τομή ενός ευθύγραμμου τμήματος ΑΒ μήκους λ μπορεί να γίνει με κανόνα και διαβήτη.

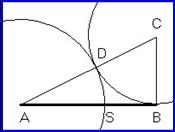Κατασκευάζουμε ένα ορθογώνιο τρίγωνο με κάθετες πλευρές ΑΒ=λ

και BC = λ/2, οπότε η υποτείνουσα AC θα είναι Ö5λ/2.

Με το διαβήτη χαράσσουμε έναν κύκλο κέντρου C και ακτίνας  λ/2,

οπότε προσδιορίζεται το σημείο D, σημείο τομής του κύκλου και

της AC. Με κέντρο το Α χαράσσουμε έναν κύκλο ακτίνας AD,

ο οποίος τέμνει την ΑΒ στο σημείο S.  Εύκολα αποδεικνύεται ότι

ΑΒ/ΑS = Ö5+1  ότι το S δηλαδή τέμνει την ΑΒ με χρυσή τομή.

 

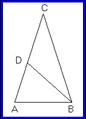Χρυσό τρίγωνο

Χρυσό λέγεται κάθε ισοσκελές  τρίγωνο στο οποίο ο λόγος

της μεγάλης πλευράς προς τη μικρή θα είναι ίσος με φ.

Κάθε ισοσκελές με γωνία κορυφής 36⁰ είναι χρυσό.

Μπορούμε να το αποδείξουμε φέρνοντας τη διχοτόμο

μιας από τις παρά τη βάση γωνίες – στο σχήμα της Β –

τα τρίγωνα ABC και ABD είναι όμοια,  οπότε (AC) = φ(AB)

Η διχοτόμος της γωνίας Β = 72⁰ δημιουργεί στην απέναντι πλευρά χρυσή τομή

 

 

Το αστέρι των Πυθαγορείων

Το σύμβολο της αδελφότητας των Πυθαγορείων ήταν το

«πεντάγραμμο», το αστέρι δηλαδή

 που σχηματίζεται από τις πέντε διαγωνίους του

κανονικού πενταγώνου. Αποδεικνύεται ότι κάθε πλευρά

του «πενταγράμμου» διαιρεί τις δύο άλλες σε χρυσή τομή.

Κάθε γωνία του «πενταγράμμου» είναι 36⁰. Στο τρίγωνο

 ΑΓΔ του σχήματος η ΓΕ διχοτομεί τη γωνία ΑΓΔ άρα τέμνει κατά χρυσή τομή την ΔΓ.

 

 

 

Χρυσό ορθογώνιο

Το χρυσό ορθογώνιο έχει λόγο των πλευρών του ίσο με φ. α/β = φ . 

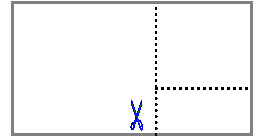Αν του αποκόψουμε ένα τετράγωνο

με πλευρά β, το ορθογώνιο με

πλευρές β, γ που θα απομείνει

θα είναι και πάλι χρυσό,

θα είναι δηλαδή β/γ = φ και

αυτό θα συνεχίζεται επ’ άπειρον.

 

Χρυσό σπιράλ, κοχύλια και ηλιοτρόπια

Εάν αντί να χρησιμοποιήσουμε το ψαλίδι σχεδιάσουμε πάνω  στο αρχικό ορθογώνιο τις τομές και

σε κάθε τετράγωνο που δημιουργείται

σχεδιάσουμε τα αντίστοιχα τεταρτοκύκλια

θα έχουμε αρχίσει να φτιάχνουμε

το χρυσό ελικοειδές, το σπιράλ

που σχεδιάζει η φύση και το διακρίνουμε

στα κουκουνάρια, στα κοχύλια,

στα ηλιοτρόπια και στους τρόπους με

τους οποίους διευθετούνται τα πέταλα, τα φύλλα και τα κλαδιά ποικίλων προσωρινών κατοίκων της γήινης βιόσφαιρας.

 

 

ΟΛΜΕ: «Οι εκπαιδευτικοί δεν χωράνε στα αμερικάνικης έμπνευσης «top-100» του Υπουργείου Παιδείας»
Tags: ΔΣ ΟΛΜΕ

ΑΝΑΚΟΙΝΩΣΗ
«Αριστεία και καινοτομία στην Εκπαίδευση»

Η διαίρεση των εκπαιδευτικών σε «καλούς» και «κακούς», η προώθηση του μεταξύ τους ανταγωνισμού και η ταύτιση των «καλών» με όσους συναινούν στην οικονομική και εκπαιδευτική πολιτική της κυβέρνησης είναι οι στόχοι που κρύβονται πίσω από τη “δράση” «Αριστεία και Καινοτομία στην εκπαίδευση».

Η διαμαρτυρία εκπαιδευτικών στη σχετική υπουργική εκδήλωση το Σάββατο 13 Μάρτη στο Ίδρυμα Μείζονος Ελληνισμού συνέβαλε στην αποκάλυψη των στόχων αυτών. Η υπουργός Παιδείας έδειξε πρώτα μπροστά όπου ήταν οι εκπαιδευτικοί που «τιμούσε» και υπηρεσιακοί παράγοντες μιλώντας για «τα πρότυπα που χρειαζόμαστε», και στη συνέχεια πίσω, όπου στέκονταν οι ωρομίσθιοι εκπαιδευτικοί που διαμαρτύρονταν μιλώντας για «τους θιασώτες της στασιμότητας». Νωρίτερα είχε αναφερθεί ότι ο διαχωρισμός έχει ήδη θεσμοθετηθεί και ότι από τη νέα χρονιά ειδικές επιτροπές του υπουργείου θα ξεχωρίζουν τα 100 πιο «καινοτόμα» σχολεία και τους 100 πιο «καινοτόμους» εκπαιδευτικούς.

Το υπουργείο και η κυβέρνηση κάνουν πως δεν καταλαβαίνουν ότι για τη συντριπτική πλειοψηφία των εκπαιδευτικών, η υπουργική βράβευση όχι μόνο δεν έχει την παραμικρή αξία, αλλά αποτελεί και προσβολή για όλους εκείνους τους συναδέλφους που δεν χωράνε στα αμερικάνικης έμπνευσης «top-100». Κάνουν πως δεν καταλαβαίνουν ότι για τους εκπαιδευτικούς η συνεργασία των συναδέλφων και όχι ο διαγκωνισμός των υποψηφίων είναι η ελπίδα του ελληνικού σχολείου. Κάνουν πως δεν καταλαβαίνουν ότι η αναγνώριση του έργου μας έρχεται μέσα από τα μάτια των μαθητών μας και των γονιών τους και όχι από επιτροπές πρόθυμων συνεργατών ενός υπουργείου που σταθερά απαξιώνει και επίμονα συκοφαντεί τους εκπαιδευτικούς.

Kάνουν πως δεν καταλαβαίνουν ότι για εμάς το σχολείο του ανταγωνισμού, της φτήνιας, της χορηγίας και των μετρήσιμων επιδόσεων δεν είναι το σχολείο του μέλλοντος, αλλά του παρελθόντος. Το σχέδιο τους αναπαράγει το σχολείο των εξετάσεων, της αμάθειας και της υποχρηματοδότησης. Αντίθετα ο αγώνας μας υπηρετεί το σχολείο της ισότητας, της αξιοπρεπούς χρηματοδότησης, της συνεργασίας και της πάλης για μια γνώση χρήσιμη στην αναζήτηση της αλήθειας, της δικαιοσύνης και της ελευθερίας. Είμαστε σίγουροι πως στον αγώνα αυτό θα είμαστε πολλοί, γιατί αυτοί που θέλουν να στερήσουν τις λαϊκές κατακτήσεις ενός ολόκληρου αιώνα δεν μπορούν να εμπνεύσουν όραμα και εκπαιδευτικό κίνημα, γιατί αυτοί που αντλούν την ποίηση τους από το παρελθόν δεν μπορούν για πολύ να ξεγελούν πολλούς.

Ποιες είναι οι επώδυνες αλλαγές που φέρνει το νέο ασφαλιστικό νομοσχέδιο
* Πάνω από δύο εκατομμύρια εργαζόμενοι θα υποστούν τις συνέπειες της ασφαλιστικής μεταρρύθμισης την οποία προωθεί η κυβέρνηση της Νέας Δημοκρατίας και η οποία προκαλεί ήδη έντονες αντιδράσεις

Επώδυνες αλλαγές, για πάνω από δύο εκατομμύρια ασφαλισμένους, επιφέρουν οι ρυθμίσεις του νομοσχεδίου του υπουργείου Απασχόλησης, με αυξήσεις ορίων ηλικίας από δύο ως πέντε χρόνια σε πολλές κατηγορίες ασφαλισμένων και ιδιαιτέρως στις μητέρες, ενώ ταυτοχρόνως προκαλούν μειώσεις κυρίως στις επικουρικές συντάξεις στις οποίες τίθεται ως «πλαφόν» το 20% της κύριας σύνταξης. Οι ρυθμίσεις θα ισχύσουν σταδιακά με έτος αφετηρίας – ανά περίπτωση – το 2009 (ένσημα για ιατροφαρμακευτική περίθαλψη), το 2010 (μητέρες) και το 2013 (γενικά όρια ηλικίας).

Το νομοσχέδιο-μαμούθ του υπουργείου Απασχόλησης με 154 άρθρα, το οποίο προκαλεί οξύτατες αντιδράσεις σχεδόν στο σύνολο των ασφαλισμένων, παρουσίασε τις προηγούμενες ημέρες η υπουργός Απασχόλησης κυρία Φάνη Πάλλη-Πετραλιά η οποία υπεραμύνθηκε των κυβερνητικών θέσεων, υποστηρίζοντας ότι παραμένουν οι κυβερνητικές δεσμεύσεις καθώς δεν θίγονται τα «γενικά όρια ηλικίας συνταξιοδότησης» και παραμένει ο τρόπος υπολογισμού των συντάξιμων αποδοχών.

Ωστόσο δεν προσδιόρισε τη χρονική ωφέλεια του ασφαλιστικού συστήματος από τα νέα μέτρα, δηλαδή την παράταση της βιωσιμότητάς του. Περιορίστηκε μόνο να δηλώσει ότι «θα δώσουν πολλές δεκαετίες στο σύστημα». Επισήμανε την αναγκαιότητα της ασφαλιστικής μεταρρύθμισης, τονίζοντας ότι το σύστημα κοινωνικής ασφάλισης είναι κοντά στα όρια της βιωσιμότητάς του και υπογράμμισε ότι όσο καθυστερούν οι αλλαγές θα καθίστανται περισσότερο επώδυνες.

* Σαρωτικές ενοποιήσεις

Το νομοσχέδιο προβλέπει σαρωτικές ενοποιήσεις Ταμείων καθώς τα 133 υπάρχοντα θα συμπυκνωθούν σε 13, από τα οποία πέντε είναι κύριας ασφάλισης, έξι επικουρικής ασφάλισης και δύο Πρόνοιας. Οι ενοποιήσεις θα αρχίσουν εντός του 2008. Για ορισμένα Ταμεία, εντός τετραμήνου από τη δημοσίευση του νόμου, και σε άλλα εντός εξαμήνου. Ο κάθε φορέας – που θα προκύπτει από τις ενοποιήσεις – θα έχει διοικητικό συμβούλιο, ενιαίες διευθύνσεις και ενιαίους ελεγκτικούς μηχανισμούς αλλά ειδικό διακριτό λογαριασμό για κάθε εντασσόμενο Ταμείο.

Ορια ηλικίας: Αυξάνεται η ηλικία συνταξιοδότησης τουλάχιστον δύο χρόνια όσον αφορά ασφαλισμένους που συνταξιοδοτούνται βάσει ειδικών διατάξεων. Το νομοσχέδιο ανατρέπει τις διατάξεις για «έξοδο» με 35ετία και 37ετία, θίγοντας τόσο τους παλαιούς (1983- 1992) όσο και τους νέους ασφαλισμένους (μετά το 1993). Χαμένοι θα βγουν τα επόμενα 15 χρόνια περίπου 225.000 ασφαλισμένοι. Οι επώδυνες αλλαγές θα αρχίσουν να σημειώνονται το 2013 και η αύξηση του ορίου ηλικίας επιτυγχάνεται με την προσθήκη εξαμήνου ανά έτος. Η συνταξιοδότηση με 35ετία θα γίνεται στην ηλικία των 60 ετών, επηρεάζοντας τους «παλαιούς» ασφαλισμένους στο ΙΚΑ και όσους ασφαλίστηκαν μετά το 1983 στα άλλα Ταμεία μισθωτών, στα Ταμεία αυτοαπασχολουμένων και στους φορείς Τύπου. Από το 2013 τα απαιτούμενα έτη αυξάνονται κατά ένα εξάμηνο ετησίως για να ανέλθουν σε 60. Επίσης όσοι διαθέτουν 37 έτη ασφάλισης θα συνταξιοδοτούνται σε ηλικία 58 ετών και όχι χωρίς όριο όπως ίσχυε ως τώρα. Από το 2013 τίθεται όριο ηλικίας και έτσι οι ασφαλισμένοι θα πρέπει υποχρεωτικά να συμπληρώσουν το 58ο έτος.

Αύξηση της ηλικίας συνταξιοδότησης κατά δύο χρόνια για «έξοδο» με 35ετία προβλέπει το ασφαλιστικό νομοσχέδιο για τους εργαζομένους στα βαρέα και ανθυγιεινά επαγγέλματα. Η αύξηση θα συνίσταται σε ένα εξάμηνο τον χρόνο και η έναρξη εφαρμογής της θα γίνει από 1ης Ιανουαρίου 2013. Δηλαδή τα νέα όρια για συνταξιοδότηση με 35ετία θα διαμορφωθούν σταδιακά στα 55 χρόνια (από 53) για μειωμένη σύνταξη και στα 57 χρόνια (από 55) για πλήρη. Αναγκαία προϋπόθεση είναι οι εργαζόμενοι να έχουν συμπληρώσει 10.500 ημέρες ασφάλισης, εκ των οποίων οι 7.500 σε βαρέα και ανθυγιεινά επαγγέλματα.

* Εργαζόμενες μητέρες

Τουλάχιστον πέντε επιπλέον χρόνια θα αναγκαστούν να εργασθούν οι μητέρες ανηλίκων. Οι αλλαγές θα επηρεάσουν πάνω από 250.000 γυναίκες τα επόμενα 20 χρόνια οι οποίες σήμερα βγαίνουν στη σύνταξη πριν από τα 55 χρόνια τους. Οι ασφαλισμένες μητέρες στα ειδικά Ταμεία από το 1983 και εντεύθεν θα συνταξιοδοτούνται στα 55 χρόνια αντί των 50 όπως ίσχυε ως τώρα. Η αύξηση θα σημειωθεί σταδιακά από το 2013 με την προσθήκη εντός έτους, κάθε χρόνο. Οι ασφαλισμένες στο ΙΚΑ από το 1993 και εντεύθεν επίσης θα συνταξιοδοτούνται στα 55ο έτος της ηλικίας τους, αλλά με αρχή το 2010. Το 55ο έτος της ηλικίας θα απαιτείται και για τις μητέρες τριών παιδιών και άνω οι οποίες σήμερα συνταξιοδοτούνται στα 20 έτη ασφάλισης, χωρίς όριο ηλικίας. Σημειώνεται ότι προϋπόθεση για τη χορήγηση της σύνταξης αποτελεί η ανηλικότητα του παιδιού στο 50ό έτος ηλικίας της μητέρας και όχι στο 55ο έτος. Δηλαδή τη σύνταξη η μητέρα τη δικαιούται ακόμη και αν στο μεσοδιάστημα το παιδί πάψει να είναι ανήλικο.

Καθιερώνεται εξάμηνη άδεια μητρότητας πέραν της άδειας λοχείας την οποία θα λαμβάνουν οι μητέρες, κατά τη διάρκεια της οποίας θα δικαιούνται τον κατώτατο μισθό και αναλογία δώρων από τον ΟΑΕΔ. Ο Οργανισμός θα αναλάβει και την απόδοση στον ασφαλιστικό φορέα των ασφαλιστικών εισφορών. Αυξάνεται ο πλασματικός χρόνος ασφάλισης των μητέρων από 4,5 σε 5 έτη με τρία παιδιά, εφόσον αποκτήθηκαν από την 1.1.2000.

Οσοι παραμένουν στην εργασία τους μετά την 35ετία και το 60ό έτος της ηλικίας λαμβάνουν επιπλέον προσαύξηση της σύνταξης κατά 3,3% για κάθε χρόνο παραμονής, με όριο τα τρία συνολικά έτη. Το ίδιο ισχύει και για τους ασφαλισμένους μετά το 1993, με τη διαφορά ότι το έτος ηλικίας είναι το 65ο αντί του 60ού. Αντιθέτως όσοι αποχωρούν νωρίτερα (πρόωρη συνταξιοδότηση) θα λαμβάνουν μειωμένη σύνταξη κατά 6% για κάθε έτος πριν από την κανονική συνταξιοδότηση, αντί του 4,5% που ισχύει σήμερα. Στο νομοσχέδιο αναφέρεται μείωση 1/200 της σύνταξης για κάθε μήνα που υπολείπεται από τη συμπλήρωση των κανονικών ορίων, αντί του 1/267 σήμερα.

* Επικουρικές συντάξεις

Μείωση των επικουρικών συντάξεων από 20% ως 50% τα επόμενα χρόνια θα επιφέρουν οι ρυθμίσεις του νομοσχεδίου για περίπου ένα εκατομμύριο ασφαλισμένους που θα λάβουν μικρότερη σύνταξη. Με το νομοσχέδιο τίθεται πλαφόν 20% των συντάξιμων αποδοχών και τα Ταμεία που υπερβαίνουν το ποσοστό αυτό θα πρέπει να προχωρήσουν σε μειώσεις οι οποίες θα αρχίσουν να σημειώνονται το 2013, διαδοχικά, σε οκτώ ισόποσες ετήσιες δόσεις. Ενδεικτικό των επιπτώσεων είναι το γεγονός ότι με βάση τα στοιχεία των εργαζομένων στα Ταμεία στο ΤΕΑΠΟΚΑ ο περιορισμός των επικουρικών συντάξεων στο 20% θα οδηγήσει σε μείωση κατά 43%.

Παροχές υγείας: Για τη θεώρηση του βιβλιαρίου υγείας θα απαιτούνται πλέον 100 αντί των 50 ενσήμων το προηγούμενο έτος.

Αναλογική σύνταξη: Παρατείνεται ως τις 31.12.2009 η χορήγηση αναλογικής σύνταξης με 3.500 ένσημα ή 11,5 έτη ασφάλισης στο 65 έτος της ηλικίας.

Λογαριασμός Αλληλεγγύης: Δημιουργείται Ασφαλιστικό Κεφάλαιο Αλληλεγγύης Γενεών, το οποίο θα χρησιμοποιηθεί μετά το 2019 για τη στήριξη του συστήματος. Από 1.1.2009 ο λογαριασμός θα χρηματοδοτείται από το 10% των ετήσιων συνολικών εσόδων από αποκρατικοποίηση Δημοσίων Επιχειρήσεων και Οργανισμών. Από το 4% επί των ετήσιων συνολικών εσόδων του ΦΠΑ. Το 10% επί του συνόλου των ετησίως εισπραττομένων ποσών από κοινωνικούς πόρους εκ των συγκεκριμένων ασφαλιστικών φορέων.

Καθιερώνεται από 1.6.2009 ο αριθμός μητρώου κοινωνικής ασφάλισης για τους άμεσα και έμμεσα ασφαλισμένους με τον οποίο θα συναλλάσσονται όλοι οι ασφαλισμένοι καθ’ όλες τις επαφές τους με το Ταμείο τους. Με τον τρόπο αυτό θα καταστούν ευκολότερες οι συναλλαγές αλλά και η διασταύρωση των στοιχείων.
Από 10,3% ως και 26,1% μειώνονται οι συντάξεις με το νέο Ασφαλιστικό

Από 10,3% ως και 26,1% μειώνονται οι κύριες και επικουρικές συντάξεις για τους ασφαλισμένους στο ΙΚΑ με τις ρυθμίσεις του νέου ασφαλιστικού νομοσχεδίου που προβλέπουν δραστικές περικοπές όχι μόνο σε όσους βγαίνουν πρόωρα στη σύνταξη αλλά κυρίως στις επικουρικές συντάξεις.

Οπως φαίνεται στον πίνακα, ασφαλισμένος στο ΙΚΑ που βγαίνει στη σύνταξη με 20 χρόνια ασφάλισης θα έχει τη μεγαλύτερη μείωση που σε ποσοστό φθάνει το 26,1%, καθώς τον πιάνουν οι διατάξεις για τις περικοπές όσων συνταξιοδοτούνται πρόωρα.

Μειωμένη όμως κατά 19,2% θα είναι και η σύνταξη των ασφαλισμένων που συνταξιοδοτούνται με 30 χρόνια ασφάλισης, καθώς αυτούς τους πιάνει η διάταξη για το «πλαφόν» 20% στις επικουρικές συντάξεις. Το νέο νομοσχέδιο προβλέπει ότι η επικουρική σύνταξη δεν μπορεί να είναι υψηλότερη από το 20% της κύριας σύνταξης.

Παρασκευή, 16 Απριλίου 2010
Στον “αέρα”οι πανελλαδικές εξετάσεις-Απεργία αποφάσισε πριν λίγο η ΟΛΜΕ

Απεργία μέσα στις πανελλαδικές εξετάσεις αποφάσισε πριν λίγο το ΔΣ της ΟΛΜΕ , αντιδρώντας στο πολυνομοσχέδιο για την παιδεία.Ειδικότερα αποφασίστηκε η πραγματοποίση:-Α.μιας 24ωρης…
απεργίας για τις 4 Μάιου , δηλαδή μία ημέρα μετά την έναρξη των πανελλαδικών εξετάσεων των υποψηφίων αποφοίτων των ΤΕΕ.

-Β, το ΔΣ της ΟΛΜΕ αποφάσισε επίσης να πραγματοποιηθούν Γενικές Συνελεύσεις των τοπικών ΕΛΜΕ στις 4 και 5 Μαίου (Γ.Σ προέδρων στις 6 Μαίου) προτείνοντας την έναρξη απεργιών την στις 14 Μαίου, ημέρα έναρξη των πανελλαδικών εξετάσεων των υποψηφίων προερχομένων από τα Ενιαία Λύκεια. Την μορφή των απεργιών , εάν θαείναι 24ωρες επαναλαμβανόμενες ή 5νθήμερες θα λάβει η Γενική Συνέλευση των προέδρων των ΕΛΜΕ.

Η απόφαση λήφθηκε με ψήφους 8-3. Δεν ψήφισαν υπέρ τα τρία μέλη της ΠΑΣΚ

Η ΑΝΑΚΟΙΝΩΣΗ ΤΗΣ ΟΛΜΕ

Το Δ.Σ. της ΟΛΜΕ αποφάσισε το παρακάτω πρόγραμμα απεργιακών κινητοποιήσεων:

1.Συμμετοχή στην 24ωρη απεργία της ΑΔΕΔΥ στις 22/4 και στα συλλαλητήρια

2.Συμμετοχή στα συλλαλητήρια στις 27/4 σε όλη την Ελλάδα

3.Συμμετοχή στις απεργιακές συγκεντρώσεις της 1ης Μάη

4.24ωρη Απεργία στις 4/5 μαζί με τη ΔΟΕ για να μην κατατεθεί το «πολυνομοσχέδιο» του Υπουργείου Παιδείας

5.Γ.Σ. των ΕΛΜΕ το επόμενο διάστημα για συζήτηση και ενημέρωση πάνω στις επιπτώσεις των μέτρων του Προγράμματος Σταθερότητας, του «πολυνομοσχεδίου» του Υπ. Παιδείας και του Ασφαλιστικού και τη στήριξη των παραπάνω κινητοποιήσεων

6.Νέες Γ.Σ. των ΕΛΜΕ 4 και 5/5 και Γ.Σ. Προέδρων των ΕΛΜΕ στις 6/5 στην οποία θα αποφασιστεί η κλιμάκωση των απεργιακών κινητοποιήσεων από τις 14/5.

Για να ακυρωθούν τα μέτρα της κυβέρνησης

Όχι στον εργασιακό μεσαίωνα

Όχι στην περικοπή μισθών και συντάξεων

Όχι στη διάλυση του Ασφαλιστικού συστήματος

Όχι στο «πολυνομοσχέδιο» του Υπουργείου Παιδείας

Όχι στο πρόγραμμα σταθερότητας

esos.gr

Αμερικανοί προβλέπουν την Ελλάδα στην Τουρκική σφαίρα επιρροής το 2050!

Δημοσιεύθηκε από olympiada στο Μαΐου 18, 2009

Ένα βιβλίο που κυκλοφόρησε τον Ιανουάριο στις ΗΠΑ από το Ινστιτούτο Stratfor, τοποθετεί τη χώρα μας το 2050 στην τουρκική σφαίρα επιρροής, σε χάρτη τον οποίο δημοσιεύει στην ιστοσελίδα του (www.stratfor.com), δίνοντας την εντύπωση ότι η Ελλάδα και η Κύπρος σταδιακά θα δορυφοροποιηθούν και θα απορροφηθούν, αφού προηγουμένως ακολουθήσουν τον δρόμο της Φινλανδοποίησης, ανίκανες να αναχαιτίσουν την επεκτατική πολιτική της Άγκυρας.
Πρόκειται για ένα έργο «γεωπολιτικής επιστημονικής φαντασίας» στο οποίο ο συγγραφέας επιχειρεί να παρουσιάσει την εξέλιξη της ανθρωπότητας μέσα από την ανάδειξη νέων παγκόσμιων δυνάμεων.
Η Τουρκία εμφανίζεται να μένει συνειδητά εκτός Ευρωπαϊκής Ένωσης και να ακολουθεί τον δρόμο της ανάδειξης της σε περιφερειακή υπερδύναμη, εκμεταλλευόμενη τη γεωγραφική της θέση και οικοδομώντας παράλληλα ισχυρές ένοπλες δυνάμεις οι οποίες αναπτύσσουν πυραύλους με πυρηνικές κεφαλές και δορυφόρους.
Με τίτλο «The Next 100 Years» (Τα επόμενα 100 χρόνια) το βιβλίο προχωρεί σε μια γεωπολιτική-γεωστρατηγική πρόβλεψη του μέλλοντος, βασιζόμενο σε αναλύσεις και στοιχεία (οικονομία, δημογραφία, περιβάλλον, εξοπλισμοί, τεχνολογία), καθώς και στις τάσεις που διαμορφώνονται σε παγκόσμια κλίμακα. Συγγραφέας του είναι ο Αμερικανός Τζωρτζ Φρίντμαν, ιδρυτής του Stratfor (Strategic Forecasting Inc.), ενός ιδιωτικού ινστιτούτου πληροφοριών που ιδρύθηκε το 1996 στο Τέξας και έχει χαρακτηρισθεί ως «σκιώδης CΙΑ».
Σύμφωνα με τα όσα αναφέρονται στο βιβλίο

, η Τουρκία θα αναδειχθεί κατά τα επόμενα 40 χρόνια ως μια από τις τέσσερις ισχυρότερες περιφερειακές δυνάμεις του κόσμου, δημιουργώντας μια εκτενή σφαίρα γεωπολιτικής επιρροής και επεκτείνοντας τα σύνορα της. Σημειώνεται εδώ ότι σήμερα η τουρκική οικονομία κατέχει τη 17η θέση παγκοσμίως και η γειτονική χώρα περιλαμβάνεται στην ομάδα των 20 πιο ισχυρών του πλανήτη (0-20).
Ο Φρίντμαν προβλέπει την αλματώδη οικονομική ανάπτυξη της Τουρκίας, η οποία θα καταστεί μια από τις 10 πλουσιότερες χώρες του πλανήτη. Η Τουρκία του 2050 θα έχει επωφεληθεί από την κατάρρευση της Ρωσικής Ομοσπονδίας, προσαρτώντας εδάφη στην περιοχή του Καυκάσου, και θα αποτελεί την ηγεμονεύουσα δύναμη στον ισλαμικό κόσμο. Μάλιστα θα έχει νικήσει στρατιωτικά τη Ρωσία σε πόλεμο το 2020, επεκτείνοντας την επιρροή της μέχρι τις ουκρανικές πεδιάδες και καταλαμβάνοντας περιοχές τις οποίες διατηρούσε τον 17ο αιώνα, επί Οθωμανικής Αυτοκρατορίας.
Ο συγγραφέας προβλέπει ότι το 2040 η Άγκυρα θα εμπλακεί σε έναν hi-tech πόλεμο, αυτή τη φορά με τις ΗΠΑ και συμμαχώντας με την Ιαπωνία. Οι ΗΠΑ θα έχουν τη βοήθεια της Μεγάλης Πολωνίας και η περιοχή των Βαλκανίων θα καταστεί το κύριο θέατρο επιχειρήσεων. Η Ελλάδα και η Κύπρος – σύμφωνα με την ανάλυση του Φρίντμαν – θα αποτελούν στόχο της νεο-οθωμανικής αυτοκρατορίας, η οποία θα συναγωνίζεται ευθέως τις ΗΠΑ και τις άλλες δυνάμεις της Ευρώπης.

Το δυσοίωνο αυτό σενάριο εκτιμά ότι η ισχυροποίηση της Τουρκίας στον στρατιωτικό και στον οικονομικό τομέα, σε συνδυασμό με τη δημογραφική ανάπτυξη, θα δημιουργήσει τις προϋποθέσεις επανεμφάνισης της οθωμανικής σφαίρας επιρροής, στην οποία σταδιακά θα ενταχθεί το σύνολο σχεδόν των παλαιών εδαφών με επίκεντρο τη Μέση Ανατολή.Ο Φρίντμαν θεωρεί ότι: «Η Τουρκία αποτελεί πλατφόρμα σταθερότητας στο χάος της Μέσης Ανατολής.

Τα Βαλκάνια, ο Καύκασος και ο αραβικός κόσμος νότια είναι ασταθή. Όσο αυξάνεται η ισχύς της Τουρκίας – της οποίας η οικονομία και ο στρατός είναι ήδη τα πιο ισχυρά στην περιοχή – θα ενισχύεται και η επιρροή της».

Ενδιαφέρον παρουσιάζει και η δημοσιοποίηση ενός χάρτη, στην ιστοσελίδα του Stratfor, στον οποίο φαίνεται ότι από όλες τις βαλκανικές χώρες μόνον η Ελλάδα (με την Κύπρο) αποτελεί μέρος του νέου τουρκικού κόσμου, ενώ η Αλβανία, το Κοσσυφοπέδιο, τα Σκόπια, και η Βοσνία-Ερζεγοβίνη ανήκουν στην «4η Ευρώπη»!
Το βιβλίο, όμως, περιέχει έναν άλλο χάρτη στον οποίο η Ελλάδα και η Κύπρος αποτελούν μαζί με το Ισραήλ τις μοναδικές χώρες που βρίσκονται εκτός της τουρκικής σφαίρας επιρροής, ενώ η Αλβανία και η Βοσνία εντός της. Η ασυμφωνία στους χάρτες αποδεικνύει τη διάσταση της «ψυχολογικής επιχείρησης», η οποία εκπορεύεται από το 5(Γ3ΐίθΓ για τους δικούς του λόγους. Κατά τον Φρίντμαν 2040 η Γερμανία θα έχει παρακμάσει, ενώ η Πολωνία θα έχει ενισχυθεί στρατηγικά από τις Η Π Α. Το βιβλίο προκαλεί με τον τρόπο ερμηνείας του μέλλοντος και εκτός των όποιων αναλύσεων χρησιμοποιείται για τη δημιουργία κλίματος, λειτουργώντας πραγματικά ως μοχλός της ΟΙΑ. Το Stratfor έχει κατορθώσει να δημιουργήσει ζήτημα μέσα σε ελάχιστο χρόνο από την έκδοση του έργου, που μεταξύ άλλων αναφέρει ότι η Ιαπωνία, το Μεξικό και η Πολωνία θα αναδειχθούν ομοίως ως παγκόσμιες περιφερειακές δυνάμεις. Η Πολωνία θα αναδειχθεί επικεφαλής ενός συνασπισμού χωρών οι οποίες θα αντιμετωπίσουν στρατιωτικά την Τουρκία το 2050. Αξίζει να τονισθεί ότι το Ισραήλ θα αποτελέσει ένα κράτος-όμηρο, πιεζόμενο ασφυκτικά από την τουρκική σφαίρα επιρροής, η οποία θα εκτείνεται από τη Λι6ύη μέχρι τον Περσικό Κόλπο, τα Βαλκάνια, τη νότια Ρωσία και την κεντρική Ασία.

Αντίπαλος της Τουρκίας σε αυτόν τον εφιαλτικό μελλοντικό κόσμο θα είναι οι ΗΠΑ, τα συμφέροντα των οποίων – σύμφωνα με τον συγγραφέα – θα αντιμετωπίσουν μια μείζονα απειλή από την τουρκική επέκταση, μετά τη ρωσική κατάρρευση. Η μορφή των «πραγμάτων που θα έλθουν» σχεδιάστηκε με δάση την αμερικανική οπτική της παγκόσμιας γεωπολιτικής, ενώ (ας μη λησμονούμε) την Ιστορία την κυβερνά το απρόβλεπτο…

Μίκης Θεοδωράκης: “Η ποιότητα του ανθρώπινου δυναμικού έπιασε πάτο”!
Αναρτήθηκε από I-DIADROMI
“Θα ήθελα να περιοριστώ στην Ελλάδα, η οποία μέσα στη γενικευμένη διεθνή οικονομική κρίση αποτελεί ξεχωριστή περίπτωση, και να πω πως ότι είμαι βαθύτατα απαισιόδοξος για το μέλλον της χώρας μας.
Κι αυτό γιατί πιστεύω ότι τα αίτια της σημερινής κρίσης είναι τόσο βαθιά και καθοριστικά, που θα χρειαστούν πάρα πολλά χρόνια για να ξεπεραστούν.
Εάν πραγματικά θέλουμε να τα ξεπεράσουμε και να προσπαθήσουμε με όλες μας τις δυνάμεις γι αυτό.
Τα αίτια αυτά συνοψίζονται σε τρεις λέξεις: Ήθος, Μόρφωση, Πολιτισμός.
Τις τελευταίες δεκαετίες έγιναν εγκλήματα κατά του λαού με τη γενίκευση της διαφθοράς και την έλλειψη ήθους σε μεγάλη κλίμακα και σε όλα τα
κοινωνικά στρώματα, την κατακόρυφη πτώση της μόρφωσης σε όλα τα επίπεδα και την υποβάθμιση έως την εξαφάνιση του πολιτισμού, ειδικά του νεοελληνικού.
Δηλαδή η ποιότητα του ανθρώπινου δυναμικού, που αποτελεί τη βάση για την πρόοδο μιας χώρας, έχει φτάσει σε πάρα πολύ χαμηλό σημείο, ώστε κάθε προσπάθεια για οικονομική ανασύνταξη και βελτίωση των κοινωνικών συνθηκών να φαντάζει, προς το παρόν, σαν άπιαστο όνειρο.
Όμως, πέραν των σκληρών ημερών που μας περιμένουν, οι εθνικοί κίνδυνοι που μας περιβάλλουν γίνονται περισσότερο απειλητικοί, λόγω ακριβώς του γενικευμένου χαμηλού επιπέδου που χαρακτηρίζει τα πλέον ζωτικά και ευαίσθητα στηρίγματα ενός λαού, γεγονός που έχει γίνει αντιληπτό από τους κάθε είδους εχθρούς μας, που δεν διστάζουν να μας απειλούν, να μας λοιδορούν και να ποδοπατούν την εθνική μας υπερηφάνεια, δηλαδή το βασικό μας στήριγμα, που μας κράτησε τελικά όρθιους μέσα από τους αιώνες.”

Μίκης Θεοδωράκης: “Η ποιότητα του ανθρώπινου δυναμικού έπιασε πάτο”!
Αναρτήθηκε από I-DIADROMI
“Θα ήθελα να περιοριστώ στην Ελλάδα, η οποία μέσα στη γενικευμένη διεθνή οικονομική κρίση αποτελεί ξεχωριστή περίπτωση, και να πω πως ότι είμαι βαθύτατα απαισιόδοξος για το μέλλον της χώρας μας.
Κι αυτό γιατί πιστεύω ότι τα αίτια της σημερινής κρίσης είναι τόσο βαθιά και καθοριστικά, που θα χρειαστούν πάρα πολλά χρόνια για να ξεπεραστούν.
Εάν πραγματικά θέλουμε να τα ξεπεράσουμε και να προσπαθήσουμε με όλες μας τις δυνάμεις γι αυτό.
Τα αίτια αυτά συνοψίζονται σε τρεις λέξεις: Ήθος, Μόρφωση, Πολιτισμός.
Τις τελευταίες δεκαετίες έγιναν εγκλήματα κατά του λαού με τη γενίκευση της διαφθοράς και την έλλειψη ήθους σε μεγάλη κλίμακα και σε όλα τα
κοινωνικά στρώματα, την κατακόρυφη πτώση της μόρφωσης σε όλα τα επίπεδα και την υποβάθμιση έως την εξαφάνιση του πολιτισμού, ειδικά του νεοελληνικού.
Δηλαδή η ποιότητα του ανθρώπινου δυναμικού, που αποτελεί τη βάση για την πρόοδο μιας χώρας, έχει φτάσει σε πάρα πολύ χαμηλό σημείο, ώστε κάθε προσπάθεια για οικονομική ανασύνταξη και βελτίωση των κοινωνικών συνθηκών να φαντάζει, προς το παρόν, σαν άπιαστο όνειρο.
Όμως, πέραν των σκληρών ημερών που μας περιμένουν, οι εθνικοί κίνδυνοι που μας περιβάλλουν γίνονται περισσότερο απειλητικοί, λόγω ακριβώς του γενικευμένου χαμηλού επιπέδου που χαρακτηρίζει τα πλέον ζωτικά και ευαίσθητα στηρίγματα ενός λαού, γεγονός που έχει γίνει αντιληπτό από τους κάθε είδους εχθρούς μας, που δεν διστάζουν να μας απειλούν, να μας λοιδορούν και να ποδοπατούν την εθνική μας υπερηφάνεια, δηλαδή το βασικό μας στήριγμα, που μας κράτησε τελικά όρθιους μέσα από τους αιώνες.”