3ος Νόμος του Νεύτωνα (Νόμος «Δράσης-Αντόδρασης»)
Όταν ένα σώμα ασκεί σε ένα δεύτερο σώμα μία δύναμη F (δράση), τότε και το δεύτερο ασκεί στο πρώτο μία ίσου μέτρου και αντίθετης φοράς δύναμη (-F)(αντίδραση).
Οι δυνάμεις λοιπόν, εμφανίζονται στη φύση πάντα κατά ζεύγη. Οι δύο αυτές δυνάμεις, ασκούνται σε διαφορετικά σώματα.
Κατηγορίες δυνάμεων
Οι δυνάμεις, χωρίζονται σε δύο κατηγορίες ανάλογα με τον αν τα σώματα που αλληλεπιδρούν ασκούν τις μεταξύ τους δυνάμεις από απόσταση ή από επαφή.
- Δυνάμεις από απόσταση (είναι μόνο οι 4 θεμελιώδεις δυνάμεις της φύσεις):
- Βαρυτικές
- Ηλεκτρομαγνητικές
- Ισχυρές πυρηνικές
- Ασθενείς πυρηνικές
- Δυνάμεις από επαφή (όλες οι άλλες):
- Τριβή
- Άνωση
- Δύναμη ελατηρίου
- Τάση του νήματος
- Δυνάμεις κρούσεων κ.α.
Σύνθεση δυνάμεων στο επίπεδο
Όταν σε ένα σώμα ασκούνται δύο δυνάμεις που σχηματίζουν γωνία μεταξύ τους, τότε η συνισταμένη δύναμη ισούται με την διαγώνιο του παραλληλογράμμου που σχηματίζουν οι δύο δυνάμεις (κανόνας του παραλληλογράμμου).
Κάθετες δυνάμεις
|
|
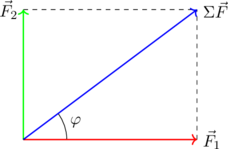
Όταν οι δυνάμεις είναι κάθετες τότε σχηματίζονται ορθογώνια τρίγωνα.
Επειδή η συνισταμένη δύναμη είναι η υποτείνουσα των τριγώνων που σχηματίζονται, μπορούμε να υπολογίσουμε το μέτρο της από το Πυθαγόρειο Θεώρημα:
![Rendered by QuickLaTeX.com \[\boxed{ΣF = \sqrt{{F_1}^2 + {F_2}^2}} \hspace{2mm} Μ\acute{ε}τρο\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-b45f707555c67d297e6a6842a9233176_l3.png)
Για να προσδιορίσουμε την κατεύθυνση της συνισταμένης δύναμης, προσδιορίζουμε την γωνία θ που σχηματίζει η συνισταμένη με την οριζόντια δύναμη F1 μέση της εφαπτομένης, δηλαδή:
![Rendered by QuickLaTeX.com \[\boxed{εφθ = \frac{F_2}{F_1}} \hspace{2mm} Διε\acute{υ}θυνση\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-910b125221d117723331e96aae428efe_l3.png)
|
Πλάγιες δυνάμεις
|
|
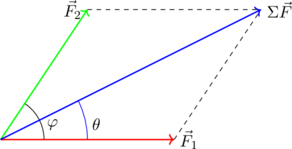
Στην περίπτωση αυτή, ο υπολογισμός της διαγωνίου γίνεται με τον νόμο των συνημιτόνων:
![Rendered by QuickLaTeX.com \[\boxed{ΣF = \sqrt{{F_1}^2 + {F_2}^2 + 2\cdot F_1 \cdot F_2 \cdot συνφ}} \hspace{2mm} Μ\acute{ε}τρο\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-285ca120ec5371bfa5e0f48528c6d826_l3.png)
Για να προσδιορίσουμε την κατεύθυνση της συνισταμένης δύναμης, προσδιορίζουμε την γωνία θ που σχηματίζει η συνισταμένη με την οριζόντια δύναμη F1 μέση της εφαπτομένης, δηλαδή:
![Rendered by QuickLaTeX.com \[εφθ = \frac{F_2\cdot ημφ}{ΣF} \]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-4c2aa2ff88237978cca5ceaa0eabbd12_l3.png)
![Rendered by QuickLaTeX.com \[\hspace{2mm} \acute{η} \hspace{2mm}\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-6742eb5f6f4d803b24589cdbb2bf078e_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{εφθ = \frac{F_2\cdot ημφ}{F_1+F_2 \cdot συνφ} } \hspace{2mm} Διε\acute{υ}θυνση\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-411f335ff02a1b9f85a10b3efcd97dcd_l3.png)
|
Όπως φαίνεται ο υπολογισμός σε αυτή την περίπτωση είναι πιο περίπλοκος και για τον λόγο αυτό δεν θα τον χρησιμοποιήσουμε φέτος αλλά θα δούμε παρακάτω κάποιους άλλους τρόπους για να συνθέτουμε πλάγιες δυνάμεις.
Ανάλυση δύναμης σε συνιστώσες
Σε πολλές περιπτώσεις είναι χρήσιμο να αναλύουμε μια δύναμη σε δύο κάθετες συνιστώσες. Δηλαδή να κάνουμε μια διαδικασία ανάποδη από την σύνθεση δύο δυνάμεων.
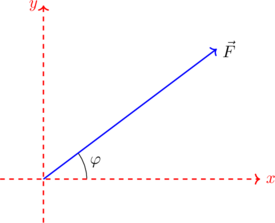
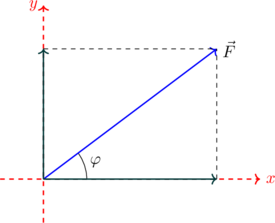
Έστω λοιπόν, σε ένα σώμα ασκείται μία δύναμη F που σχηματίζει γωνία φ με το οριζόντιο επίπεδο.
| Για να την αναλύσουμε σε συνιστώσες ακολουθούμε την παρακάτω διαδικασία. |

|
| 1. Επιλέγουμε σύστημα κάθετων αξόνων πάνω στους οποίους θα αναλύσουμε την δύναμη. |
|
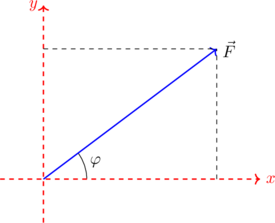
| 2. Από την κορυφή της δύναμης (βελάκι) φέρουμε παράλληλες (διακεκομμένες) γραμμές στους άξονες μέχρι να τμήσουν τους άξονες. |
|
| 3. Στα σημεία που τέμνουν οι (διακεκομμένες) γραμμές τους άξονες βάζουμε βελάκια. (Αυτές είναι οι δύο συνιστώσες της δύναμής μας) |
|
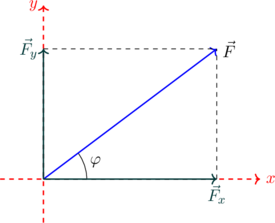
| 4. Ονομάζουμε τις δύο συνιστώσες με το όνομα της αρχικής δύναμης προσθέτοντας ως δείκτη το x ή y ανάλογα τον άξονα πάνω στον οποίο είναι η συνιστώσα. |
|
| 5. Υπολογίζουμε τις συνιστώσες από τους τριγωνομετρικούς αριθμούς της γνωστής γωνίας (ημ, συν).
Και οι δύο γωνίες είναι ίσες με την F πολλαπλασιασμένη με το ημίτονο ή το συνημίτονο της γωνίας φ.Η δύναμη που είναι προσκείμενη (ακουμπάει) της γωνίας φ έχει το συνημίτονο ενώ αυτή που είναι απέναντι από την γωνία φ έχει το ημίτονο.
ΠΡΟΣΟΧΗ!!! : Πρέπει να προσέχουμε ποια είναι η γωνία που γνωρίζουμε. Αν γνωρίζαμε την γωνία που σχηματίζει η F με τον άξονα y τότε οι Fx και Fy θα ήταν ανάποδα. |
![Rendered by QuickLaTeX.com \[\boxed{F_x = F\cdot συνφ}\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-973d7007d2801e7ad981312468f2f6a0_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{F_y = F\cdot ημφ}\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-80692f75c8b89c45b18783139f2ddbb4_l3.png)
|
TIP!!! : Ένας εύκολος τρόπος να βρίσκουμε τις σχέσεις για τις Fx και Fy είναι ο εξής: παρατηρούμε ποια από τις δύο συνιστώσες (Fx ή Fy) είναι προσκείμενη (ακουμπάει) πάνω στην γωνία που ξέρουμε. Τότε αυτή η συνιστώσα θα έχει το συνημίτονο ενώ ή άλλη το ημίτονο.
Σύνθεση πολλών ομοεπιπέδων δυνάμεων
Για να προσθέσουμε πολλές ομοεπίπεδες δυνάμεις πρέπει να έχουμε κατανοήσει καλά τα βασικά εργαλεία της ανάλυσης δύναμης, σύνθεσης συγγραμμικών δυνάμεων και σύνθεση καθέτων δυνάμεων.
Η διαδικασία που ακολουθούμε για την σύνθεση πολλών δυνάμεων που είναι στο ίδιο επίπεδο, είναι πολύ σημαντική καθώς την διαδικασία αυτή την χρησιμοποιούμε σε πολλές περιπτώσεις όπως θα δούμε.
Η διαδικασία που ακολουθούμε είναι η εξής:
- Επιλέγουμε ένα σύστημα αξόνων (x-y) όπως μας βολεύει καλύτερα
(συνήθως έτσι ώστε οι περισσότερες δυνάμεις να είναι πάνω στους άξονες).
- Αναλύουμε όλες τις δυνάμεις που δεν είναι πάνω στους άξονες και υπολογίζουμε τις συνιστώσες.
- Υπολογίζουμε την συνισταμένη δύναμη σε κάθε άξονα χωριστά (ΣFx, ΣFy) και τις σχεδιάζουμε.
- Υπολογίζουμε και σχεδιάζουμε την συνισταμένη δύναμη (ΣF) προσθέτοντας τις κάθετες συνισταμένες των αξόνων (ΣFx, ΣFy) με τον κανόνα του παραλληλογράμμου. Δηλαδή
![Rendered by QuickLaTeX.com \[\boxed{ΣF = \sqrt{{ΣF_x}^2+{ΣF_y}^2} } \hspace{2mm} και \hspace{2mm} \boxed{εφφ = \frac{ΣF_y}{ΣF_x}}\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-08997a83f5bc6381e6b28a24c9eb6ba6_l3.png)
Βέβαια υπάρχουν περιπτώσεις που μπορεί να είναι πιο “έξυπνο” να προσθέσουμε δύο δυνάμεις και μετά το αποτέλεσμά τους με την επόμενη, όμως αυτό το κάνουμε μόνο σε πολύ ειδικές περιπτώσεις και για αυτό δεν τα αναλύουμε εδώ παραπάνω.
Παράδειγμα
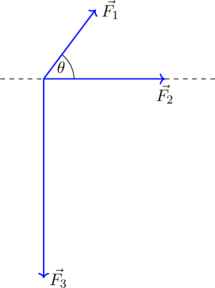
Να υπολογιστεί η συνισταμένη δύναμη των δυνάμεων αν γνωρίζουμε ότι:
F1 = 20Ν ,
F2 = 28Ν,
F3 = 46Ν
και για τη γωνία θ ισχύει: ημθ=0,8 και συνθ=0,6. |
|
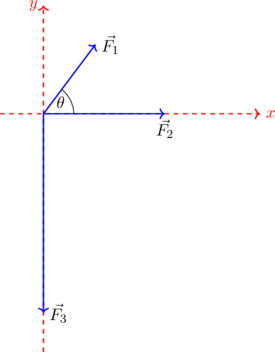
| Βήμα 1: Επιλέγουμε σύστημα αξόνων(x,y) |
|
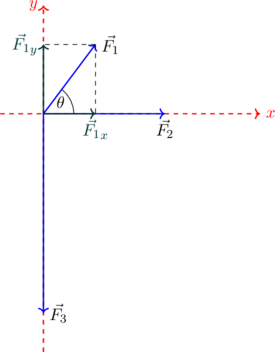
| Βήμα 2: Αναλύουμε την δύναμη F1 (που δεν είναι πάνω στους άξονες) σε συνιστώσες:
![Rendered by QuickLaTeX.com \[{F_1}_x &= F_1 \cdot συνθ = 20 \cdot 0.6 \Longrightarrow \boxed{ {F_1}_x &= 12 N }\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-f38532288da51f6ef2ef2463ed898bd7_l3.png)
![Rendered by QuickLaTeX.com \[{F_1}_y &= F_1 \cdot ημθ =20 \cdot 0.8 \Longrightarrow \boxed{{F_1}_y &= 16 N }\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-34dd6959e01849e269fedfb74f046d02_l3.png)
|
|
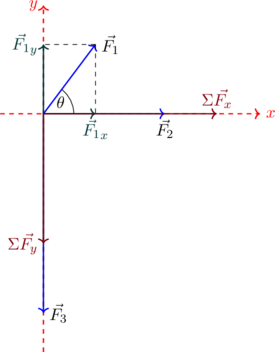
| Βήμα 3: Υπολογίζουμε και σχεδιάζουμε τη συνισταμένη σε κάθε άξονα:
![Rendered by QuickLaTeX.com \[ΣF_x = {F_1}_x + F_2 = 12 + 28 \Longrightarrow \boxed{ΣF_x = 40 N}\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-2a0ae6d3cb8d83419adea6b4afa06b28_l3.png)
![Rendered by QuickLaTeX.com \[ΣF_y = {F_1}_y - F_3 = 16 - 46 \Longrightarrow \boxed{ΣF_x = -30 N}\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-bd3205dd0b9bb29d9ddc786485bfaf17_l3.png)
|
|
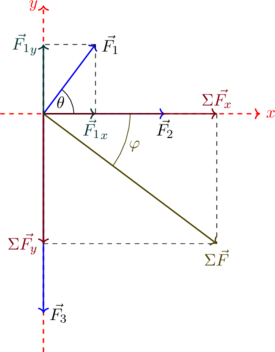
| Βήμα 4: Υπολογίζουμε και σχεδιάζουμε τη συνισταμένη δύναμη από τις δύο κάθετες συνιστώσες:
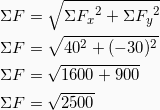
![Rendered by QuickLaTeX.com \[\boxed{ΣF = 50N}\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-d8597dbb2b5f83413ab593a19d5a6e76_l3.png)
και
![Rendered by QuickLaTeX.com \[εφφ = \frac{ΣF_y}{ΣF_x} = \frac{-30}{40}=-\frac{3}{4} = -0,75\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-172d58a0811770f7607f290b9331510c_l3.png)
|
|
Ο Νόμος της Τριβής
Στο Γυμνάσιο ορίσαμε την τριβή (Τ) ως τη δύναμη που ασκείται μεταξύ δύο σωμάτων που είναι σε επαφή και το ένα κινείται ή τείνει να κινηθεί ως προς το άλλο. Όπως θα δούμε εδώ, δεν υπάρχει μόνο ένα είδος τριβής.
ΣΗΜΕΙΩΣΗ: όταν λέμε ότι στο σώμα “κινείται” εννοούμε γλιστράει/ολισθάινει!
Όταν το σώμα τείνει να κινηθεί αλλά δεν κινείται, τότε η Τριβή ονομάζεται Στατική Τριβή και για να την υπολογίσουμε εφαρμόζουμε τη συνθήκη ισορροπίας για το σώμα.
Όταν το σώμα μόλις ξεκινάει να κινηθεί ι, τότε η Τριβή ονομάζεται Οριακή Τριβή.
Όταν το σώμα κινείται, τότε η Τριβή ονομάζεται Τριβή Ολίσθησης και υπολογίζεται από την σχέση:
![Rendered by QuickLaTeX.com \[\boxed{Τ = μ\cdot Ν }\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-7070e3c2485447576a1df14abc25cc9b_l3.png)
όπου:
- Ν: η κάθετη αντίδραση του επιπέδου
- μ: ο συντελεστής τριβής μεταξύ σώματος και επιπέδου.
Η παραπάνω σχέση ισχύει και για την τριβή ολίσθησης αλλά και για την οριακή τριβή. Πρέπει όμως να έχουμε στο μυαλό μας, ότι ο συντελεστής τριβής είναι διαφορετικός σε κάθε περίπτωση με μορ ≥ μολ..
Βέβαια θα δούμε ότι πολλές φορές θεωρούμε ότι οι δύο αυτοί συντελεστές είναι ίσοι.












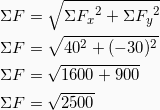


 Άρθρα (RSS)
Άρθρα (RSS)