Science & Education

24 10 2020

Λυμένη Άσκηση

Αναρτήθηκε από Παναγιώτης Κουτεντάκης στο Φυσική Α' Λυκείου

Άσκηση

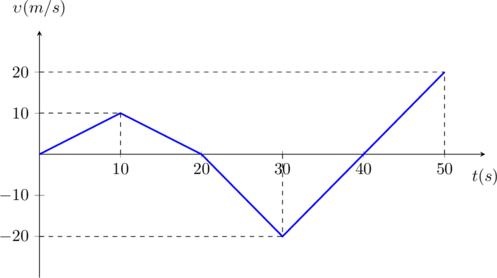
Ένα σώμα κινείται ευθύγραμμα και η ταχύτητά του δίνεται από το παρακάτω διάγραμμα.

Rendered by QuickLaTeX.com

Να προσδιορίσετε το είδος των κινήσεων του σώματος.
Να υπολογίσετε την επιτάχυνση και την μετατόπιση του σώματος σε κάθε κίνηση.
Να υπολογίσετε την συνολική του μετατόπιση καθώς και το διάστημα το οποίο διένυσε.
Να υπολογίσετε την μέση ταχύτητα του σώματος.
Να γίνουν τα διαγράμματα επιτάχυνσης – χρόνου, διαστήματος – χρόνου και θέσης – χρόνου.

Λύση

1. και 2. Για κάθε κίνηση μπορούμε να υπολογίσουμε την επιτάχυνση από την κλίση της ευθείας ενώ την μετατόπιση από το εμβαδόν του διαγράμματος με τον άξονα των χρόνων.

(0s – 10s): Ευθύγραμμη Ομαλά Επιταχυνόμενη Κίνηση

$\alpha_1 = \frac{\Delta \upsilon}{\Delta t} = \frac{\upsilon_{10} - \upsilon_0}{t_{10}-t_0}=\frac{10-0}{10-0}=\frac{10}{10} \Longrightarrow \boxed{\alpha_1 = 1m/s^2}$

$\Delta x_1 = E_{\tau \rho \iota \gamma .} = \frac{1}{2}\cdot \beta \cdot \upsilon = \frac{1}{2}\cdot10 \cdot 10 \Longrightarrow \boxed{\Delta x_1 = 50m}$

(10s – 20s): Ευθύγραμμη Ομαλά Επιβραδυνόμενη Κίνηση (μέχρι να μηδενιστεί η ταχύτητά του)

$\alpha_2 = \frac{\Delta \upsilon}{\Delta t} = \frac{\upsilon_{20} - \upsilon_{10}}{t_{20}-t_{10}}=\frac{0-20}{20-10}=\frac{-20}{10} \Longrightarrow \boxed{\alpha_2 = -1m/s^2}$

$\Delta x_2 = E_{\tau \rho \iota \gamma .} = \frac{1}{2}\cdot \beta \cdot \upsilon = \frac{1}{2}\cdot (20-10) \cdot 10 = \frac{1}{2}\cdot 10 \cdot 10 \Longrightarrow \boxed{\Delta x_2 = 50m}$

(20s – 30s): Ευθύγραμμη Ομαλά Επιταχυνόμενη Κίνηση (με αρνητική φορά)

Από τη στιγμή που η ταχύτητα του σώματος έχει μηδενιστεί, δεν γίνεται να επιβραδύνει άλλο. Άρα επιταχύνεται προς την αρνητική φορά.

$\alpha_3 = \frac{\Delta \upsilon}{\Delta t} = \frac{\upsilon_{30} - \upsilon_{20}}{t_{30}-t_{20}}=\frac{-20-0}{30-20} = \frac{-20}{10} \Longrightarrow \boxed{\alpha_3 = -2m/s^2}$

$\Delta x_3 = E_{\tau \rho \iota \gamma .} = \frac{1}{2}\cdot \beta \cdot \upsilon = \frac{1}{2}\cdot (30-20) \cdot (-20) = \frac{1}{2}\cdot 10 \cdot (-20) \Longrightarrow \boxed{\Delta x_3 = -100m}$

(30s – 40s): Ευθύγραμμη Ομαλά Επιβραδυνόμενη Κίνηση (με αρνητική φορά)

$\alpha_4 = \frac{\Delta \upsilon}{\Delta t} = \frac{\upsilon_{40} - \upsilon_{30}}{t_{40}-t_{30}}=\frac{0-(-20)}{40-30} =\frac{20}{10}\Longrightarrow \boxed{\alpha_4 = 2m/s^2}$

$\Delta x_4 = E_{\tau \rho \iota \gamma .} = \frac{1}{2}\cdot \beta \cdot \upsilon = \frac{1}{2}\cdot (40-30) \cdot (-20) = \frac{1}{2}\cdot 10 \cdot (-20) \Longrightarrow \boxed{\Delta x_4 = -100m}$

(40s – 50s): Ευθύγραμμη Ομαλά Επιταχυνόμενη Κίνηση

$\alpha_5 = \frac{\Delta \upsilon}{\Delta t} = \frac{\upsilon_{50} - \upsilon_40}{t_{50}-t_{40}}=\frac{20-0}{50-40}=\frac{20}{10} \Longrightarrow \boxed{\alpha_5 = 2m/s^2}$

$\Delta x_5 = E_{\tau \rho \iota \gamma .} = \frac{1}{2}\cdot \beta \cdot \upsilon = \frac{1}{2}\cdot20 \cdot 10 \Longrightarrow \boxed{\Delta x_5 = 100m}$

3. Η συνολική μετατόπιση του σώματος θα ισούται με το άθροισμα των επιμέρους μετατοπίσεων. δηλαδή:

$\Delta x_{o \lambda .} = \Delta x_1 + \Delta x_2 + \Delta x_3 +\Delta x_4 + \Delta x_5 +\Delta x_6 \Longrightarrow$

$\Delta x_{o \lambda .}= 50+50+(-100)+(-100)+100 \Longrightarrow \boxed{\Delta x_{o \lambda .} = 0m}$

Το συνολικό διάστημα που θα διένυσε το σώμα θα ισούται με το άθροισμα των απολύτων τιμών των επιμέρους μετατοπίσεων. δηλαδή:

$s = |\Delta x_1| + |\Delta x_2| + |\Delta x_3| +|\Delta x_4| + |\Delta x_5| +|\Delta x_6| \Longrightarrow$

$s= 50+50+100+100+100 \Longrightarrow \boxed{s = 400m}$

4. Η μέση ταχύτητα του σώματος θα είναι:

$\upsilon_{\mu} = \frac{s}{t} = \frac{400}{50} \Longrightarrow \boxed{\upsilon_{\mu} = 8m/s}$

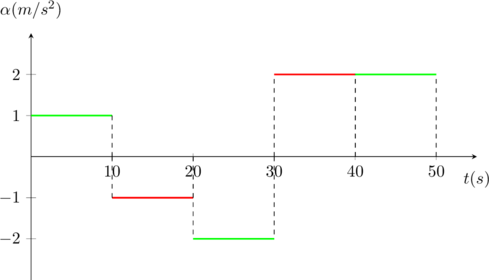
5. Το διάγραμμα επιτάχυνσης – χρόνου θα είναι:

Rendered by QuickLaTeX.com

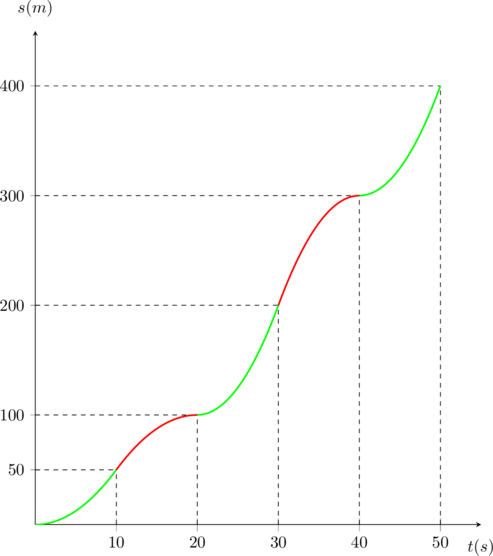
Το διάγραμμα διαστήματος – χρόνου θα είναι:

Rendered by QuickLaTeX.com

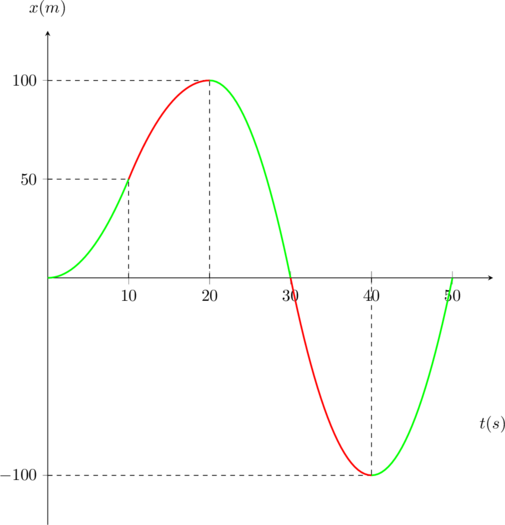
Το διάγραμμα θέσης – χρόνου θα είναι:

Rendered by QuickLaTeX.com

Αυτή η εργασία έχει άδεια χρήσης Creative Commons -Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή4.0.

Το άρθρο δημοσιεύτηκε Σάββατο 24 Οκτωβρίου 2020 στις 00:10 στην κατηγορία Φυσική Α' Λυκείου. Μπορείς να παρακολουθείς τα σχόλια χρησιμοποιώντας το RSS 2.0 feed. Τα σχόλια και τα pings δεν επιτρέπονται.

Τα σχόλια είναι κλειστά.

Open your mind…

Λυμένη Άσκηση

Σελίδες