« 
 »
17 03 2020

Δυναμική σε μια διάσταση

Αναρτήθηκε από Παναγιώτης Κουτεντάκης στο Φυσική Α' Λυκείου

 

Η έννοια της δύναμης

 

Η δύναμη μπορεί να προκαλέσει:

  1. μεταβολή στην κινητική κατάσταση (ταχύτητα) ενός σώματος
  2. παραμόρφωση ενός σώματος

 

Η δύναμη είναι διανυσματικό φυσικό μέγεθος άρα για να την προσδιορίσουμε χρειαζόμαστε το μέτρο της και την κατεύθυνσή της (διεύθυνση και φορά)

Το σύνηθες σύμβολο για τη δύναμη είναι το F ενώ η μονάδα μέτρησής της, είναι το 1Ν(=Kg.m/s2) (Νιούτον – Newton)

 

Οι δυνάμεις πάντα εμφανίζονται στην φύση ανά δύο (κατά ζεύγη)

Όταν ένα σώμα Α ασκεί δύναμη σε ένα σώμα Β τότε και το Β ασκεί δύναμη στο σώμα Α. Τα σώματα λέμε τότε ότι αλληλεπιδρούν.

 

Οι δυνάμεις χωρίζονται σε δύο μεγάλες κατηγορίες, τις δυνάμεις:

  1.  από απόσταση (Βαρυτικές, Μαγνητικές, Ηλεκτρικές)
  2. από επαφή  (Τριβή, Άνωση, Ελατηρίου, τεντωμένου σχοινιού, σωμάτων που συγκρούονται κ.α.)

 

Νόμος του Hooke

“Η επιμήκυνση ενός ελατηρίου είναι ανάλογη της δύναμης που ασκείται σε αυτό”.

Στον νόμο του Hook στηρίζεται η κατασκευή των οργάνων μέτρησης των δυνάμεων που ονομάζονται δυναμόμετρα.

Το μέτρο της δύναμης συνδέεται με την επιμήκυνση του ελατηρίου με τη σχέση:

    \[\boxed{F = k\cdot x}\]

όπου:

F: η δύναμη που ασκεί το ελατήριο,

x: η επιμήκυνση του ελατηρίου και

k: ονομάζεται σταθερά του ελατηρίου που μας δείχνει πόσα Νιούτον χρειάζονται για να προκληθεί επιμήκυνση 1 μέτρου στο ελατήριο (είναι ο συντελεστής αναλογίας των δύο μεγεθών). Η μονάδα μέτρησης του k είναι Ν/m.

 

 

Σύνθεση συγγραμμικών δυνάμεων

 

Όταν σε ένα σώμα ασκούντα,στο ίδιο σημείο, δύο ή περισσότερες συγγραμμικές δυνάμεις, μπορούμε να τις αντικαταστήσουμε με μία που να προκαλεί το ίδιο αποτέλεσμα. Η συνολική αυτή δύναμη ονομάζεται συνισταμένη δύναμη ενώ οι δυνάμεις τις οποίες αντικαταστήσαμε ονομάζονται συνιστώσες της. Την συνισταμένη δύναμη της συμβολίζουμε συνήθως με ΣF ή Fολ..

Η διαδικασία με την οποία υπολογίζουμε την συνισταμένη δύναμη από τις συνιστώσες, ονομάζεται σύνθεση δυνάμεων.

Καλό είναι να θυμόμαστε πως σε κάθε περίπτωση η συνισταμένη δύναμη είναι το διανυσματικό άθροισμα των συνιστωσών της, δηλαδή:

    \[Σ\vec{F} = \vec{F}_1 + \vec{F}_2 + \cdots\]

 

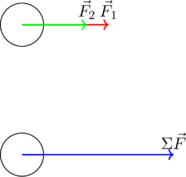
Σύνθεση δύο ομόρροπων δυνάμεων

Rendered by QuickLaTeX.com

 Όταν σε ένα σώμα ασκούνται δύο ομόρροπες δυνάμεις, τότε η συνισταμένη δύναμη έχει την κατεύθυνση των δυνάμεων και μέτρο ίσο με το άθροισμα των μέτρων των συνιστωσών. Δηλαδή:

    \[\boxed{ΣF = F_1 + F_2}\]

Το ίδιο κάνουμε αν στο σώμα ασκούνται περισσότερες από δύο ομόρροπες δυνάμεις. Δηλαδή:

    \[\boxed{ΣF = F_1 + F_2 + F_3 + \cdots}\]

 

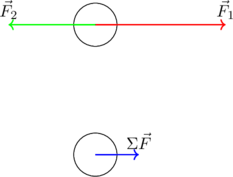
Σύνθεση δύο αντίρροπων δυνάμεων

 

Rendered by QuickLaTeX.com

 Όταν σε ένα σώμα ασκούνται δύο αντίρροπες δυνάμεις, τότε η συνισταμένη δύναμη έχει την κατεύθυνση της συνσιτώσας με το μεγαλύτερο μέτρο και μέτρο ίσο με διαφορά των μέτρων των συνιστωσών. Δηλαδή:

    \[\boxed{ΣF = F_1 - F_2}\]

 

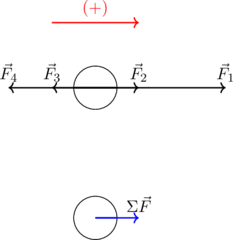
Σύνθεση πολλών συγγραμμικών δυνάμεων

Όταν σε ένα σώμα ασκούνται περισσότερες από δύο συγγραμμικές δυνάμεις, τότε για να υπολογίσουμε την συνισταμένη δύναμη μπορούμε να εργαστούμε με δύο τρόπους.

1ος Τρόπος

Rendered by QuickLaTeX.com
  1. Ορίζουμε θετική φορά (όποια θέλουμε εμείς)
  2. Γράφουμε την διανυσματική σχέση για το άθροισμα της συνισταμένης δύναμης

        \[Σ\vec{F} = \vec{F}_1 + \vec{F}_2 +\vec{F}_3 +\vec{F}_4\]

  3. Αντικαθιστούμε τα διανύσματα με τις αλγεβρικές τιμές των δυνάμεων ανάλογα με την κατεύθυνσή τους (όσες έχουν φορά ίδια με την θετική φορά τις βάζουμε θετικές ενώ τις άλλες αρνητικές)

        \[ΣF = F_1 + F_2 - F_3 - F_4\]

  4. Υπολογίζουμε την αλγεβρική τιμή της συνισταμένης δύναμης
  5. Σχεδιάζουμε την συνισταμένη δύναμη ανάλογα με το πρόσημό της.

 

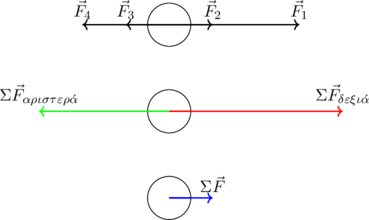
2ος Τρόπος

Rendered by QuickLaTeX.com
  1. Βρίσκουμε την συνισταμένη των δυνάμεων που είναι προς την μία κατεύθυνση (π.χ. δεξιά ΣFδεξια) και την σχεδιάζουμε.

        \[ΣF_{δεξι\acute{α}} = F_1 + F_2\]

  2. Βρίσκουμε την συνισταμένη των δυνάμεων που είναι προς την άλλη κατεύθυνση (π.χ. αριστερά ΣFαριστερά) και την σχεδιάζουμε.

        \[ΣF_{αριστερ\acute{α}} = F_3 + F_4\]

  3. Βρίσκουμε την συνισταμένη δύναμη των δύο αντίρροπων δυνάμεων που βρήκαμε και την σχεδιάζουμε.

        \[\boxed{ΣF = ΣF_{δεξι\acute{α}} - ΣF_{αριστερ\acute{α}}}\]

Είναι καλύτερο σε αυτή τη φάση να χρησιμοποιούμε τον 1ο τρόπο καθώς η κατανόησή του θα μας βοηθήσει στο επόμενο κεφάλαιο.

 

1ος Νόμος του Νεύτωνα

 

Αδράνεια ονομάζουμε την ιδιότητα των σωμάτων να αντιστέκονται σε κάθε μεταβολή της κινητικής τους κατάστασης.

Στη φυσική, όταν ένα σώμα ισορροπεί τότε παραμένει ακίνητο ή κινείται με σταθερή ταχύτητα. Δηλαδή:

    \[Ισορροπ\acute{ι}α \Longleftrightarrow \left . \begin{cases} \vec{υ} = 0 \hspace{5mm} (ακ\acute{ι}νητο)\\ \vec{υ} = σταθ. \hspace{5mm} (ΕΟΚ) \end{cases} \right .\]

Ο 1ος νόμος του Νεύτωνα περιγράφει τι συμβαίνει όταν σε ένα σώμα δεν ασκείται καμία δύναμη, ή αν η συνισταμένη των δυνάμεων που ασκούνται πάνω στο σώμα είναι μηδέν. Σύμφωνα με τον 1ο νόμο του Νεύτωνα:

“Αν η συνισταμένη των δυνάμεων που ασκούνται σε ένα σώμα είναι μηδέν, τότε το σώμα ή ηρεμεί ή κινείται ευθύγραμμα και ομαλά”.

Ένα άλλος τρόπος που θα μπορούσε να διατυπωθεί ο 1ος νόμος του Νεύτωνα είναι:

“Αν η συνισταμένη των δυνάμεων που ασκούνται σε ένα σώμα είναι μηδέν, τότε το σώμα ισορροπεί”.

Ο 1ος νόμος μπορεί να γραφεί με τη μορφή σχέσης ως εξής:

    \begin{align*} Σ\vec{F} = 0 &\Longleftrightarrow Ισορροπ\acute{ι}α \\ \acute{η}\\ Σ\vec{F} = 0 &\Longleftrightarrow \left . \begin{cases} \vec{υ} = 0 \hspace{5mm} (ακ\acute{ι}νητο)\\ \vec{υ} = σταθ. \hspace{5mm} (ΕΟΚ) \end{cases} \right . \end{align*}

 

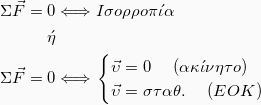
2ος Νόμος του Νεύτωνα (Θεμελιώδης Νόμος της Μηχανικής)

 

Ο 2ος νόμος του Νεύτωνα περιγράφει τι συμβαίνει όταν σε ένα σώμα  η συνισταμένη των δυνάμεων που ασκούνται πάνω του δεν είναι μηδέν.

Σύμφωνα με τον 2ο νόμο του Νεύτωνα, όταν σε ένα σώμα η συνισταμένη δύναμη δεν είναι μηδέν, τότε το σώμα αποκτά επιτάχυνση η οποία είναι ανάλογη της συνισταμένης δύναμης και αντιστρόφως ανάλογη της μάζας του σώματος.

Ο 2ος νόμος μπορεί να γραφεί πολύ απλά με τη μορφή σχέσης ως εξής:

    \[\boxed{ Σ\vec{F} = m\cdot \vec{α}}\]

Παρατηρώντας την παραπάνω σχέση, μπορούμε να ξεχωρίσουμε 3 περιπτώσεις:

  1. Αν η συνισταμένη δύναμη είναι μηδέν (ΣF=0), τότε και η επιτάχυνση του σώματος θα είναι μηδέν, άρα το σώμα ή θα παραμένει ακίνητο ή θα κινείται ευθύγραμμα και ομαλά (1ος Νόμος Νεύτωνα).
  2. Αν η συνισταμένη δύναμη είναι σταθερή (ΣF= σταθ.), τότε και η επιτάχυνση του σώματος θα είναι σταθερή, άρα το σώμα θα εκτελεί Ευθύγραμμη Ομαλά Μεταβαλλόμενη Κίνηση.
  3. Αν η συνισταμένη δύναμη δεν είναι σταθερή, τότε και η επιτάχυνση δεν θα είναι σταθερή, άρα το σώμα θα εκτελεί μια πιο σύνθετη κίνηση.

Βάρος – Μάζα

 

Βάρος (Β ή w)

Βάρος ονομάζουμε την βαρυτική δύναμη που ασκεί η Γη (ή κάποιο άλλο σώμα με μεγάλη μάζα) σε κάθε σώμα που βρίσκεται κοντά της. Καθώς είναι δύναμη, το Βάρος είναι διάνυσμα με κατεύθυνση προς το κέντρο της Γης και η μονάδα μέτρησής του είναι το Νιούτον (N).

Το βάρος αλλάζει από τόπο σε τόπο, και μειώνεται όσο αυξάνεται η απόσταση του σώματος από το κέντρο της Γης.

Για μικρά ύψη από την επιφάνεια της Γης, το βάρος συνδέεται με την μάζα με της σχέση:

    \[ \vec{B} = m\cdot \vec{g}\]

όπου g η επιτάχυνση της βαρύτητας στην επιφάνειας της Γης.

 

Μάζα (m)

Η μάζα είναι θεμελιώδες μονόμετρο φυσικό μέγεθος και είναι το μέτρο της αδράνειας ενός σώματος (αδρανειακή μάζα).

Η μάζα ενός σώματος παραμένει σταθερή και δεν μεταβάλλεται από τόπο σε τόπο.

 

Διαφορές μάζας – βάρους

Μάζα Βάρος
Σύμβολο

    \[ m\]

    \[\vec{B} \hspace{5mm}\acute{η} \hspace{5mm}\vec{w}\]
Ορισμός Το μέτρο της αδράνειας ενός σώματος Η βαρυτική δύναμη που ασκεί η Γη
Μονάδα μέτρησης kg (Χιλιόγραμμο) Ν (Νιούτον)
Είδος Μονόμετρο Διανυσματικό
Όργανο μέτρησης Ζυγός Δυναμόμετρο
  Παραμένει σταθερή σε κάθε τόπο Αλλάζει από τόπο σε τόπο
Σχέση

    \[Β = m\cdot g \]

 

 

Ελεύθερη πτώση

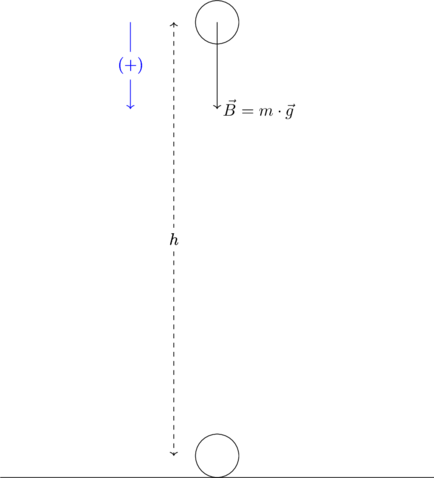
Ελεύθερη πτώση ονομάζουμε την κίνηση που κάνει ένα σώμα αν το αφήσουμε από κάποιο ύψος και πάνω του επιδρά μόνο η δύναμη του βάρους.

Rendered by QuickLaTeX.com

Σύμφωνα με τον 2ο νόμο του Νεύτωνα θα ισχύει (Θεωρούμε θετική φορά προς τα κάτω):

    \begin{align*} ΣF &=m\cdot α &\Longleftrightarrow\\ B &= m\cdot a & \Longleftrightarrow \\ m\cdot g &= m\cdot α & \Longrightarrow\\ \frac{\cancel{m} \cdot a}{\cancel{m}} &= \frac{\cancel{m}\cdot g}{\cancel{m}} &\Longleftrightarrow \end{align*}

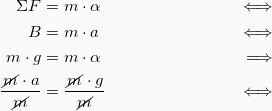
(1)   \begin{equation*} \boxed{α = g} \end{equation*}

Το σώμα λοιπόν, εκτελεί Ευθύγραμμη Ομαλά Επιταχυνόμενη Κίνηση, χωρίς αρχική ταχύτητα, με επιτάχυνση ίση με την επιτάχυνση της βαρύτητας (g).

Επομένως, οι εξισώσεις που θα περιγράφουν την κίνηση του σώματος θα είναι:

Ταχύτητα: 

(2)   \begin{equation*} \boxed{υ = g\cdot t} \end{Equation}
Μετατόπιση: 

(3)   \begin{equation*} \boxed{\Delta y = \frac{1}{2}\cdot g\cdot t^2} \end{Equation}

 

Μετά από πόσο χρόνο θα πέσει το σώμα στο έδαφος;

Όταν το σώμα φτάσει στο έδαφος θα έχει διανύσει απόσταση h άρα η μετατόπισή του θα είναι:

    \begin{align*} \Delta y &= h & \Longrightarrow\\ \frac{1}{2}\cdot g \cdot t_{εδ\acute{a}φους}^2 &= h &\Longrightarrow\\ g\cdot t_{εδ\acute{a}φους}^2 &= 2\cdot h & \Longrightarrow\\ \frac{\cancel{g}\cdot t_{εδ\acute{a}φους}^2}{\cancel{g}} &= \frac{2\cdot h}{g} &\Longrightarrow\\ t_εδ\acute{a}φους^2 &= \frac{2\cdot h}{g} &\Longrightarrow\\ \end{align*}

(4)   \begin{equation*} \boxed{t_{εδ\acute{a}φους} = \sqrt{\frac{2\cdot h}{g}}} \end{equation*}

Με τι ταχύτητα θα φτάσει το σώμα στο έδαφος;

Αφού το σώμα χρειάζεται χρόνο tεδάφους να φτάσει στο έδαφος, η ταχύτητα που θα έχει όταν φτάσει στο έδαφος θα είναι:

    \begin{align*} υ_{εδ\acute{a}φους} &= g\cdot t_{εδ\acute{a}φους} &\Longrightarrow\\ υ_{εδ\acute{a}φους} &= g\cdot \sqrt{\frac{2\cdot h}{g}}& \Longrightarrow\\ υ_{εδ\acute{a}φους} &= \sqrt{\frac{g^2\cdot 2\cdot h}{g}}& \Longrightarrow\\ υ_{εδ\acute{a}φους} &= \sqrt{\frac{ g^{\cancel{2}} \cdot 2 \cdot h }{\cancel{g}}} &\Longrightarrow\\ \end{align*}

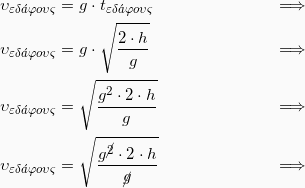
(5)   \begin{equation*} \boxed{υ_{εδ\acute{a}φους} &= \sqrt{2 \cdot g\cdot h}} \end{equation*}

Εδώ θα βρείτε μερικά παραδείγματα ασκήσεων στην Ελεύθερη Πτώση.

 

Κατακόρυφη Βολή προς τα Κάτω

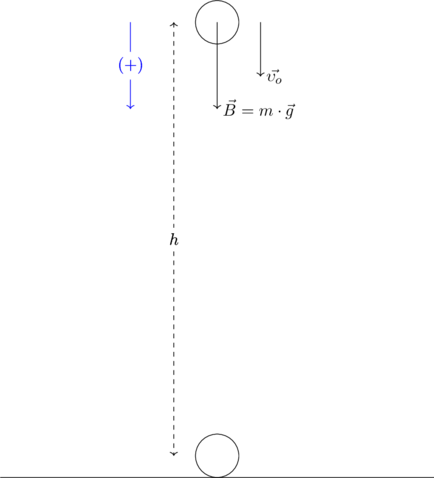
Κατακόρυφη Βολή προς τα κάτω ονομάζουμε την κίνηση που κάνει ένα σώμα αν το εκτοξεύσουμε με μία αρχική ταχύτητα (προς τα κάτω) από κάποιο ύψος και πάνω του επιδρά μόνο η δύναμη του βάρους.

Rendered by QuickLaTeX.com

Σύμφωνα με τον 2ο νόμο του Νεύτωνα θα ισχύει (Θεωρούμε θετική φορά προς τα κάτω):

    \begin{align*} ΣF &=m\cdot α &\Longleftrightarrow\\ B &= m\cdot a & \Longleftrightarrow \\ m\cdot g &= m\cdot α & \Longrightarrow\\ \frac{\cancel{m} \cdot a}{\cancel{m}} &= \frac{\cancel{m}\cdot g}{\cancel{m}} &\Longleftrightarrow \end{align*}

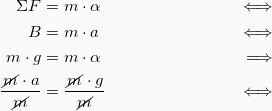
(6)   \begin{equation*} \boxed{α = g} \end{equation*}

Το σώμα λοιπόν, εκτελεί Ευθύγραμμη Ομαλά Επιταχυνόμενη Κίνηση, με αρχική ταχύτητα και επιτάχυνση ίση με την επιτάχυνση της βαρύτητας (g).

Επομένως, οι εξισώσεις που θα περιγράφουν την κίνηση του σώματος θα είναι:

Ταχύτητα: 

(7)   \begin{equation*} \boxed{υ =υ_{ο} + g\cdot t} \end{Equation}
Μετατόπιση: 

(8)   \begin{equation*} \boxed{\Delta y = υ_{ο}\cdot t + \frac{1}{2}\cdot g\cdot t^2} \end{Equation}

 

Εδώ θα βρείτε μερικά παραδείγματα ασκήσεων στην Κατακόρυφη βολή προς τα κάτω.

 

 

Κατακόρυφη Βολή προς τα Πάνω

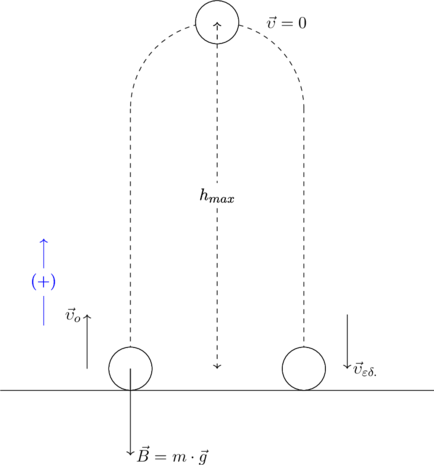
Κατακόρυφη Βολή προς τα πάνω ονομάζουμε την κίνηση που κάνει ένα σώμα αν το εκτοξεύσουμε με μία αρχική ταχύτητα (προς τα πάνω), είτε από το έδαφος είτε από κάποιο ύψος, και πάνω του επιδρά μόνο η δύναμη του βάρους.

Rendered by QuickLaTeX.com

Σύμφωνα με τον 2ο νόμο του Νεύτωνα θα ισχύει (Θεωρούμε θετική φορά προς τα πάνω):

    \begin{align*} ΣF &=m\cdot α &\Longleftrightarrow\\ -B &= m\cdot a & \Longleftrightarrow \\ -m\cdot g &= m\cdot α & \Longrightarrow\\ \cancel{-}\frac{\cancel{m} \cdot a}{\cancel{-m}} &= \frac{\cancel{m}\cdot g}{-\cancel{m}} &\Longleftrightarrow \end{align*}

(9)   \begin{equation*} \boxed{α = -g} \end{equation*}

Το σώμα λοιπόν, εκτελεί Ευθύγραμμη Ομαλά Επιβραδυνόμενη Κίνηση, με αρχική ταχύτητα και επιτάχυνση ίση με την επιτάχυνση της βαρύτητας (g).

Επομένως, οι εξισώσεις που θα περιγράφουν την κίνηση του σώματος θα είναι:

Ταχύτητα: 

(10)   \begin{equation*} \boxed{υ =υ_{ο} - g\cdot t} \end{Equation}
Μετατόπιση: 

(11)   \begin{equation*} \boxed{\Delta y = υ_{ο}\cdot t - \frac{1}{2}\cdot g\cdot t^2} \end{Equation}

 

Εδώ θα βρείτε μερικά παραδείγματα ασκήσεων στην Κατακόρυφη βολή προς τα πάνω.

 

CC BY 4.0 Αυτή η εργασία έχει άδεια χρήσης Creative Commons Αναφορά δημιουργού4.0.

Το άρθρο δημοσιεύτηκε Τρίτη 17 Μαρτίου 2020 στις 15:53 στην κατηγορία Φυσική Α' Λυκείου. Μπορείς να παρακολουθείς τα σχόλια χρησιμοποιώντας το RSS 2.0 feed. Τα σχόλια και τα pings δεν επιτρέπονται.

Τα σχόλια είναι κλειστά.
Αλλαγή μεγέθους γραμματοσειράς
Αντίθεση
Accessibility by WAH
Μετάβαση σε γραμμή εργαλείων