Άσκηση 1
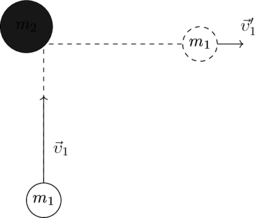
Σώμα μάζας m1=4kg, που είναι δεμένο με νήμα μήκους l=2m αφήνεται να πέσει από ύψος h=0,2m όπως φαίνεται στο σχήμα. Όταν το νήμα είναι κατακόρυφο συγκρούεται με ακίνητο σώμα μάζας m2=2kg. Μετά την κρούση το σώμα μάζας m1 κινείται με ταχύτητα ίδιας κατεύθυνσης με πριν και μέτρο ίσο με το μισό της ταχύτητας που είχε πριν την κρούση. Το σώμα μάζας m2 σταματάει αφού έχει διανύσει απόσταση x=10m πάνω στο επίπεδο.
Να υπολογίσετε:
- Την ταχύτητα του σώματος m1 λίγο πριν την κρούση.
- Την δύναμη που δέχεται το σώμα m1 κατά την κρούση αν η διάρκειά της είναι Δt = 0,01s.
- Την τάση του νήματος τη στιγμή της κρούσης.
- Το έργο της δύναμης που δέχεται το σώμα m2 κατά την κρούση.
- Τον συντελεστή τριβής του m2 με το οριζόντιο επίπεδο.
(Δίνεται g=10m/s2)
Λύση
1. Εφαρμόζουμε Αρχή Διατήρησης της Μηχανικής Ενέργειας από την αρχική θέση του σώματος m1 μέχρι τη στιγμή που το νήμα γίνεται κατακόρυφο κι έχουμε:
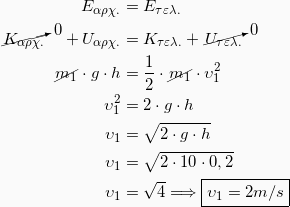
2. Τη δύναμη που δέχεται το σώμα m1 κατά την κρούση θα το βρούμε εφαρμόζοντας τη γενίκευση του 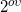 Νόμου του Νεύτωνα, δηλαδή:
Νόμου του Νεύτωνα, δηλαδή:
(1) 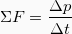
Γνωρίζουμε επίσης ότι μετά την κρούση το σώμα m1 έχει ταχύτητα ίδιας κατεύθυνσης με την αρχική και μέτρου ίσου με το μισό της αρχικής, δηλαδή:
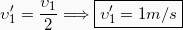
Αντικαθιστώντας τις ορμές στην 1, έχουμε:
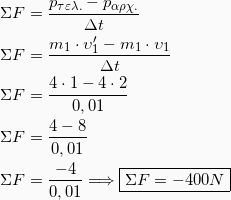
3. Την στιγμή της κρούσης, το σώμα m1 είναι κατακόρυφο και οι δυνάμεις που ασκούνται πάνω του είναι η Τάση του νήματος (προς τα πάνω) και το βάρος (προς τα κάτω).
Η συνισταμένη των δύο αυτών δυνάμεων θα πρέπει να παίζει τον ρόλο της κεντρομόλου δύναμης που αναγκάζει το σώμα να εκτελεί κυκλική κίνηση. Άρα θα πρέπει:
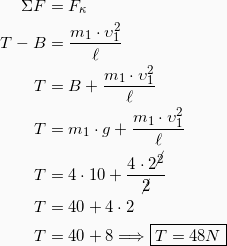
4. Επειδή η δύναμη δεν είναι σταθερή ούτε γνωρίζουμε την μετατόπιση κατά την κρούση, ο μόνος τρόπος για να υπολογίσουμε το έργο της δύναμης που δέχεται το σώμα m2 κατά την κρούση είναι με Θεώρημα Μεταβολής της Κινητικής Ενέργειας. Έχουμε λοιπόν:
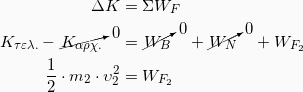
Άρα:
(2) 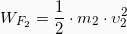
Για να βρούμε την ταχύτητα του m2 μετά την κρούση, θα εφαρμόσουμε την Αρχή Διατήρησης της Ορμής για την κρούση οπότε θα έχουμε:
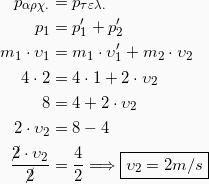
Αντικαθιστώντας τώρα στην 2 έχουμε:
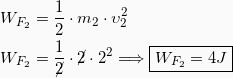
5. Όπως γνωρίζουμε
![Rendered by QuickLaTeX.com \[Τ = μ\cdot N\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-bf7c6316033ea972e80c890775d95931_l3.png)
,
άρα μπορούμε να υπολογίσουμε τον συντελεστή τριβής αν γνωρίζουμε την Τριβή (Τ)και την Κάθετη αντίδραση του επιπέδου (Ν). Δηλαδή:
(3) 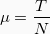
Επειδή το σώμα ισορροπεί στον κατακόρυφο άξονα ισχύει ότι:
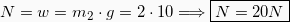 .
.
Την τριβή μπορούμε να την υπολογίσουμε εφαρμόζοντας το Θεώρημα Μεταβολής της Κινητικής Ενέργειας από τη θέση της κρούσης μέχρι τη θέση που σταματάει το σώμα m2. Έχουμε λοιπόν:
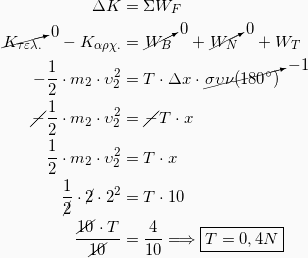
Αντικαθιστώντας στην 3 παίρνουμε:
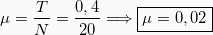
Άσκηση 2
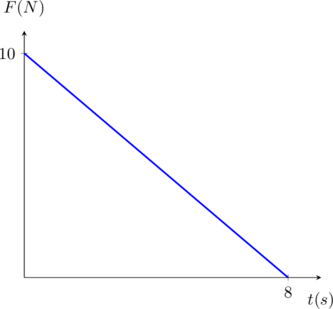
Σώμα μάζας m=2kg κινείται σε λείο οριζόντιο επίπεδο με σταθερή ταχύτητα υo=10m/s. Τη χρονική στιγμή to=0 αρχίζει να ασκείται πάνω του οριζόντια δύναμη ομόρροπη της ταχύτητας το μέτρο της οποίας μεταβάλλεται όπως φαίνεται στο διάγραμμα.
Να υπολογίσετε:
- Την μεταβολή της ορμής του σώματος για το χρονικό διάστημα 0s – 8s.
- Την ταχύτητα του σώματος τη χρονική στιγμή t=8s.
- Το έργο της δύναμης F που δέχθηκε το σώμα.
Λύση
1. Από τη γενίκευση του 2ου Νόμου του Νεύτωνα βλέπουμε ότι η μεταβολή της ορμής δίνεται από το γινόμενο της δύναμης με το χρόνο, δηλαδή:
![Rendered by QuickLaTeX.com \[ΣF = \frac{Δp}{Δt} \Longleftrightarrow Δp = ΣF \cdot Δt\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-846f26c045cca3fbca503c683cbde775_l3.png)
Από το διάγραμμα Δύναμης – χρόνου, το εμβαδόν μας δίνει την μεταβολή της ορμής.
Άρα:
![Rendered by QuickLaTeX.com \[Δp = Εμβαδ\acute{o}ν_Τριγ\acute{\omega}νου} = \frac{(β\acute{α}ση)\cdot (\acute{υ}ψος)}{2} = \frac{8\cdot10}{2} \Longrightarrow\\ \boxed{Δp = 40 kg\cdot m/s}\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-03338345620ed086f1e95e3774e5c46d_l3.png)
2. Από τη στιγμή που ξέρουμε την μεταβολή της ορμής το σώματος, μπορούμε να υπολογίσουμε την ορμή του στο τέλος των 8 δευτερολέπτων:
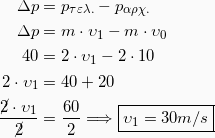
3.
Καθώς η δύναμη δεν είναι σταθερή ούτε ξέρουμε την εξάρτησή της από την μετατόπιση του σώματος, ο μόνος τρόπου για να υπολογίσουμε το έργο της είναι από το Θεώρημα Μεταβολής της Κινητικής Ενέργειας, δηλαδή:
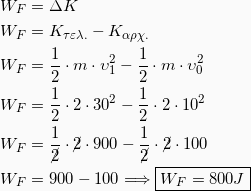
Άσκηση 3
Σφαίρα μάζας m1=1kg κινείται με ταχύτητα υ1 = 12m/s σε οριζόντιο επίπεδο και συγκρούεται με ακίνητη σφαίρα μάζας m2=2kg. Μετά την κρούση η σφαίρα μάζας m1 κινείται κάθετα προς την αρχική της διεύθυνση με ταχύτητα υ1‘ = 5m/s.
Να υπολογίσετε:
- Την μεταβολή της ορμής του σώματος μάζας m1.
- Την ταχύτητα που θα αποκτήσει το σώμα μάζας m2.
- Την θερμότητα που παράχθηκε κατά την κρούση.
Λύση
1. Η μεταβολή της ορμής του σώματος m1 θα είναι:
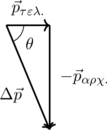
Επειδή οι ορμές πριν και μετά την κρούση δεν είναι συγγραμμικές, πρέπει να αφαιρέσουμε διανυσματικά τις δύο ορμές.
Έχουμε δηλαδή για το μέτρο της
![Rendered by QuickLaTeX.com \[Δ\vec{p}\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-4473d91101fe3b0cfdc6748f10f5910a_l3.png)
:
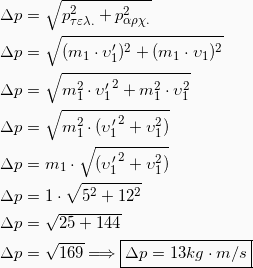
Η διεύθυνση της μεταβολής της ορμής θα σχηματίζει με τον οριζόντιο άξονα γωνία θ τέτοια ώστε:
![Rendered by QuickLaTeX.com \[εφ(θ) = \frac{p_{αρχ.}}{p_{τελ.}} = \frac{12}{5} =2,4 \Longrightarrow θ\simeq 67,4^\circ\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-ac43605a733fd3055ae9779b300c3301_l3.png)
2. Επειδή έχουμε κρούση, θα ισχύει η Αρχή Διατήρησης της Ορμής, οπότε η μεταβολή της ορμής του σώματος m2 θα είναι αντίθετη της μεταβολής της ορμής του σώματος m1.
Το σώμα λοιπόν θα κινηθεί σε διεύθυνση αντίθετη με την Δp1 με ορμή που θα έχει μέτρο ίσο με το μέτρο της Δp1.
Η ταχύτητά του, λοιπόν, μετά την κρούση θα είναι:
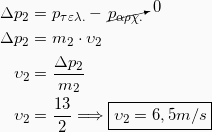
3. Η θερμότητα που θα παραχθεί κατά την κρούση θα είναι η Κινητική Ενέργεια που χάθηκε κατά τη διάρκεια της κρούσης. Δηλαδή:
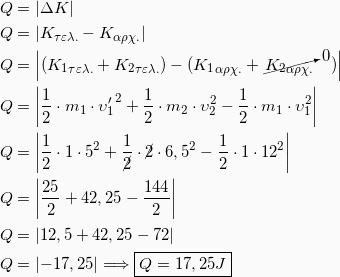
Το μείον μέσα στο απόλυτο μας δείχνει ότι χάθηκε ενέργεια κατά την κρούση.


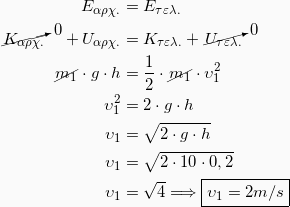
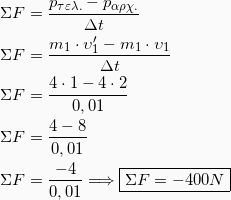
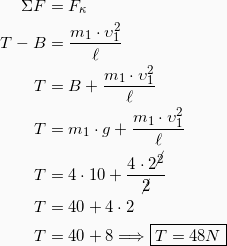
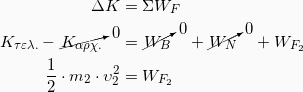
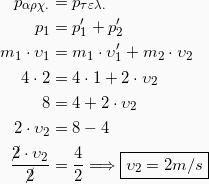
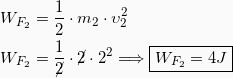
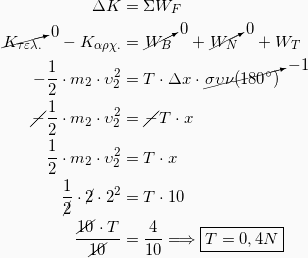
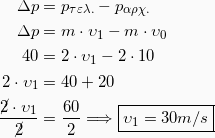
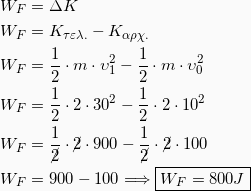
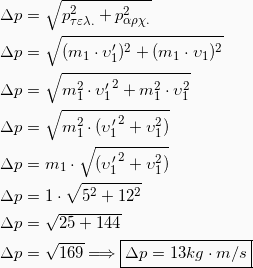
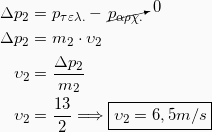
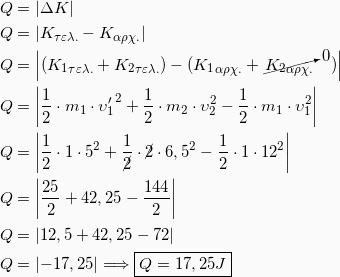
 Άρθρα (RSS)
Άρθρα (RSS)