Παράδειγμα 1
Ένα αρχικά ακίνητο σώμα ξεκινά να επιταχύνει σταθερά και μετά από 3 δευτερόλεπτα έχει αναπτύξει ταχύτητα 12m/s.
- Να υπολογίσετε την επιτάχυνση του σώματος.
- Να υπολογίσετε την ταχύτητα του σώματος μετά από 10 δευτερόλεπτα.
- Να υπολογίσετε το διάστημα που διένυσε το σώμα στο 10ο δευτερόλεπτο της κίνησής του.
- Να γίνουν τα διαγράμματα επιτάχυνσης – χρόνου, ταχύτητας – χρόνου και μετατόπισης χρόνου για τα 10 πρώτα δευτερόλεπτα της κίνησης του σώματος.
Λύση
1. Από την εκφώνηση της άσκησης βλέπουμε ότι η αρχική ταχύτητα του σώματος θα είναι μηδέν, δηλαδή:
![]()
Η επιτάχυνση του σώματος μπορεί να υπολογιστεί από τον ορισμό της. Δηλαδή:
![]()
Οι εξισώσεις, λοιπόν, που θα περιγράφουν την κίνηση του σώματος θα είναι:
2. Η ταχύτητα του σώματος μετά από 10 δευτερόλεπτα θα είναι:
![]()
3. Το 10ο δευτερόλεπτο της κίνησης του σώματος είναι μεταξύ 9 και 10 s. Το διάστημα που θα διανύσει το σώμα κατά τότε θα είναι η διαφορά της μετατόπισής του στα 10s μείον την μετατόπιση στα 9s. Άρα:
![]()
![]()
Άρα:
![]()
4.
Διάγραμμα επιτάχυνσης – χρόνου
|
|
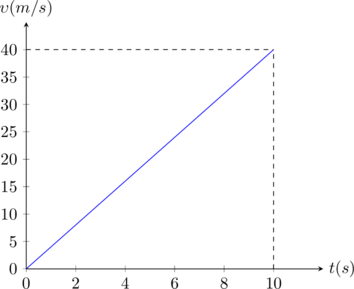
Διάγραμμα ταχύτητας – χρόνου
|
|
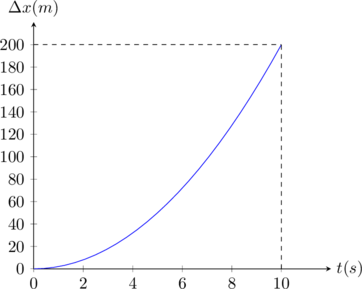
Διάγραμμα μετατόπισης – χρόνου
|
|
Παράδειγμα 2
Η θέση ενός σώματος που κινείται ευθύγραμμα δίνεται από την παρακάτω σχέση:
![]()
- Να βρεθεί η επιτάχυνση και η αρχική ταχύτητα του σώματος και να γραφεί η εξίσωση της ταχύτητας.
- Να υπολογίσετε ποια χρονική στιγμή θα σταματήσει στιγμιαία το σώμα.
- Να υπολογίσετε το διάστημα που θα διανύσει το σώμα μέχρι να σταματήσει.
- Να γίνουν τα διαγράμματα επιτάχυνσης – χρόνου, ταχύτητας – χρόνου και θέσης χρόνου μέχρι να σταματήσει το σώμα.
Λύση
1. Παρατηρούμε ότι η σχέση που μας δίνεται για τη θέση του σώματος είναι της μορφής
![]()
Άρα το σώμα κάνει ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση.
Συγκρίνοντας τη σχέση που μας δίνεται με την σχέση της θέσης για την επιβραδυνόμενη κίνηση βγάζουμε ότι:
![]()
και
![]()
Συνεπώς η εξίσωση που θα δίνει την ταχύτητα του σώματος θα είναι:
![]()
2. Όταν το σώμα σταματήσει, η ταχύτητά του θα είναι μηδέν. Άρα:
![]()
3. Το διάστημα που θα διανύσει το σώμα μέχρι να σταματήσει (t=20s) θα είναι το ίδιο με την θέση του εκείνη την στιγμή (καθώς η αρχική του θέση είναι μηδέν). Άρα:
![]()
4.
Διάγραμμα επιτάχυνσης – χρόνου
|
|
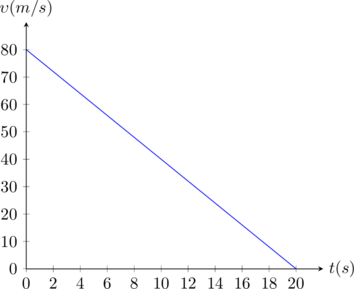
Διάγραμμα ταχύτητας – χρόνου
|
|
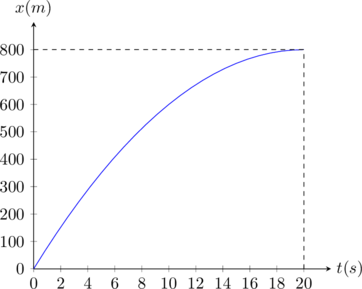
Διάγραμμα θέσης – χρόνου
|
|
Παράδειγμα 3
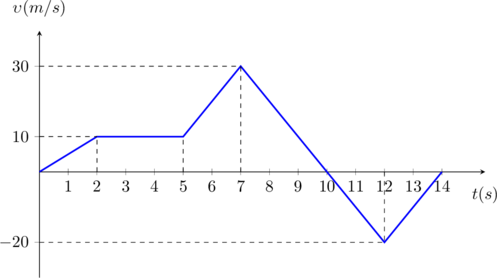
Ένα σώμα κινείται ευθύγραμμα και η ταχύτητά του δίνεται από το παρακάτω διάγραμμα.
|
|
- Να προσδιορίσετε το είδος των κινήσεων του σώματος.
- Να υπολογίσετε την επιτάχυνση και την μετατόπιση του σώματος σε κάθε κίνηση.
- Να υπολογίσετε την συνολική του μετατόπιση καθώς και το διάστημα το οποίο διένυσε.
- Να υπολογίσετε την μέση ταχύτητα του σώματος.
- Να γίνουν τα διαγράμματα επιτάχυνσης – χρόνου, διαστήματος – χρόνου και θέσης – χρόνου.
Λύση
1. και 2. Για κάθε κίνηση μπορούμε να υπολογίσουμε την επιτάχυνση από την κλίση της ευθείας ενώ την μετατόπιση από το εμβαδόν του διαγράμματος με τον άξονα των χρόνων.
(0s – 2s): Ευθύγραμμη Ομαλά Επιταχυνόμενη Κίνηση
![]()
![]()
(2s – 5s): Ευθύγραμμη Ομαλή Κίνηση
![]()
![]()
(5s – 7s): Ευθύγραμμη Ομαλά Επιταχυνόμενη Κίνηση
![]()
![]()
(7s – 10s): Ευθύγραμμη Ομαλά Επιβραδυνόμενη Κίνηση (μέχρι να μηδενιστεί η ταχύτητά του)
![]()
![]()
(10s – 12s): Ευθύγραμμη Ομαλά Επιταχυνόμενη Κίνηση (με αρνητική φορά)
Από τη στιγμή που η ταχύτητα του σώματος έχει μηδενιστεί, δεν γίνεται να επιβραδύνει άλλο. Άρα επιταχύνεται προς την αρνητική φορά.
![]()
![]()
(12s – 14s): Ευθύγραμμη Ομαλά Επιβραδυνόμενη Κίνηση (με αρνητική φορά)
![]()
![]()
3. Η συνολική μετατόπιση του σώματος θα ισούται με το άθροισμα των επιμέρους μετατοπίσεων. δηλαδή:
![]()
![]()
Το συνολικό διάστημα που θα διένυσε το σώμα θα ισούται με το άθροισμα των απολύτων τιμών των επιμέρους μετατοπίσεων. δηλαδή:
![]()
![]()
4. Η μέση ταχύτητα του σώματος θα είναι:
![]()
5. Το διάγραμμα επιτάχυνσης – χρόνου θα είναι:
|
|
Το διάγραμμα διαστήματος – χρόνου θα είναι:
|
|
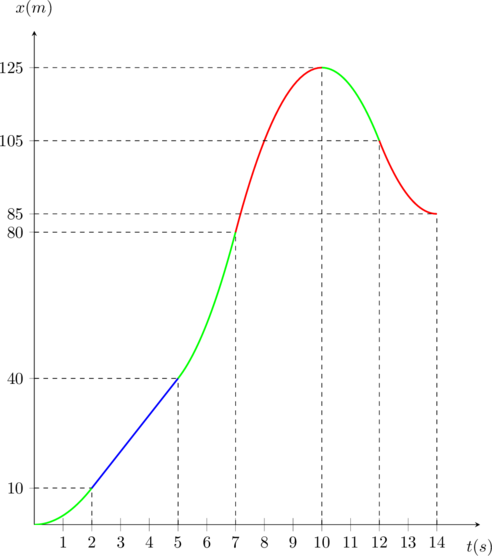
Το διάγραμμα θέσης – χρόνου θα είναι:
|
|
Παρατηρούμε ότι τα δύο διαγράμματα διαφέρουν μετά τα 10s γιατί το σώμα κινείται προς τα πίσω οπότε η θέση του μειώνεται ενώ το διάστημα συνεχίζει να αυξάνει.
Παράδειγμα 4
Ένα αυτοκίνητο και μία μηχανή κινούνται σε ευθύγραμμο δρόμο. Τη χρονική στιγμή μηδέν, η μηχανή βρίσκεται σε απόσταση d=200m πίσω από το αυτοκίνητο και κινείται με ταχύτητα 50m/s, πατάει φρένο κι αρχίζει να επιβραδύνει με επιβράδυνση αμ= 2m/s2. Το αυτοκίνητο κινείται με σταθερή ταχύτητα 20m/s.
- Ποια χρονική στιγμή τα δύο οχήματα έχουν την ίδια ταχύτητα;
- Να δειχθεί ότι τα οχήματα θα συναντηθούν δύο φορές.
- Ποια θα είναι η ταχύτητα της μηχανής όταν συναντήσει το αυτοκίνητο;
- Ποια η μετατόπιση των δύο οχημάτων όταν συναντιούνται;
- Να γίνουν τα διαγράμματα ταχύτητας – χρόνου, μετατόπισης – χρόνου και θέσης – χρόνου για τα δύο οχήματα σε κοινό σύστημα αξόνων.
Λύση
Γράφουμε τις σχέσεις που περιγράφουν την κίνηση των σωμάτων:
| Αυτοκίνητο | Μηχανή | |
| Είδος κίνησης | Ε.Ο.Κ. | Ε.Ο.Επιβ.Κ. |
| Ταχύτητα | ||
| Μετατόπιση |
Στη συνέχεια κάνουμε σχήμα με τα σώματα στην αρχική και τελική τους θέση και σημειώνουμε τις μετατοπίσεις τους και τις αποστάσεις που δίνονται και ζητούνται.
|
|
1. Όταν τα σώματα έχουν την ίδια ταχύτητα ισχύει:
![]()
![]()
![]()
2. Όταν τα σώματα συναντιούνται ισχύει (από το σχήμα):
![]()
![]()
![]()
Λύνουμε την δευτεροβάθμια εξίσωση:
![]()
Άρα έχουμε δύο λύσεις:
![Rendered by QuickLaTeX.com \[t_{1,2} = \frac{-\beta\pm \sqrt{\Delta}}{2\cdot \alpha} = \frac{-(-30)\pm \sqrt{100}}{2 \cdot 1} = \frac{30\pm 10}{2} = \left . \begin{cases} t_1 =\frac{20}{2} \Rightarrow \boxed{t_1=10s}\\ t_2 =\frac{40}{2} \Rightarrow \boxed{t_2=20s} \end{cases} \right .\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-20b586e0575ed543cf2cc165a412ee48_l3.png)
Επειδή και οι δύο λύσεις είναι θετικές τις δεχόμαστε, άρα τα οχήματα θα συναντηθούν δύο φορές μία τη χρονική στιγμή t1 = 10s και ξανά μετά τη χρονική στιγμή t2 = 20s.
3. Η ταχύτητα της μηχανής όταν συναντήσει το αυτοκίνητο θα είναι:
4. Οι μετατοπίσεις των οχημάτων όταν συναντιούνται θα είναι:
5.
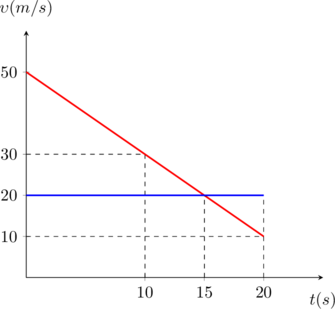
Διάγραμμα ταχύτητας – χρόνου
|
|
Διάγραμμα μετατόπισης – χρόνου
|
|
Διάγραμμα θέσης – χρόνου
|
|
Στο διάγραμμα θέσης – χρόνου φαίνεται καθαρά ότι τα δύο σώματα συναντιούνται δύο φορές (στα σημεία τομής των δύο γραμμών).
![]() Αυτή η εργασία έχει άδεια χρήσης Creative Commons -Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή4.0.
Αυτή η εργασία έχει άδεια χρήσης Creative Commons -Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή4.0.










 Άρθρα (RSS)
Άρθρα (RSS)