Η δύναμη μπορεί να προκαλέσει:
- μεταβολή στην κινητική κατάσταση (ταχύτητα) ενός σώματος
- παραμόρφωση ενός σώματος
Η δύναμη είναι διανυσματικό φυσικό μέγεθος άρα για να την προσδιορίσουμε χρειαζόμαστε το μέτρο της και την κατεύθυνσή της (διεύθυνση και φορά)
Το σύνηθες σύμβολο για τη δύναμη είναι το F ενώ η μονάδα μέτρησής της, είναι το 1Ν(=Kg.m/s2) (Νιούτον – Newton)
Το όργανο με το οποίο μετράμε μία δύναμη είναι το δυναμόμετρο.
Οι δυνάμεις πάντα εμφανίζονται στην φύση ανά δύο (κατά ζεύγη)
Όταν ένα σώμα Α ασκεί δύναμη σε ένα σώμα Β τότε και το Β ασκεί δύναμη στο σώμα Α. Τα σώματα λέμε τότε ότι αλληλεπιδρούν.
Οι δυνάμεις χωρίζονται σε δύο μεγάλες κατηγορίες, τις δυνάμεις:
- από απόσταση (Βαρυτικές, Μαγνητικές, Ηλεκτρικές)
- από επαφή (Τριβή, Άνωση, Ελατηρίου, τεντωμένου σχοινιού, σωμάτων που συγκρούονται κ.α.)
Νόμος του Hooke
Η επιμήκυνση ενός ελατηρίου είναι ανάλογη της δύναμης που ασκείται σε αυτό.
Στον νόμο του Hook στηρίζεται η κατασκευή των οργάνων μέτρησης των δυνάμεων που ονομάζονται δυναμόμετρα.
Η δύναμη συνδέεται με την επιμήκυνση του ελατηρίου με τη σχέση:
![]()
όπου:
![]() : η δύναμη που ασκεί το ελατήριο,
: η δύναμη που ασκεί το ελατήριο,
![]() : η επιμήκυνση του ελατηρίου και
: η επιμήκυνση του ελατηρίου και
![]() : ονομάζεται σταθερά του ελατηρίου που μας δείχνει πόσα Νιούτον χρειάζονται για να προκληθεί επιμήκυνση 1 εκατοστό στο ελατήριο (είναι ο συντελεστής αναλογίας των δύο μεγεθών)
: ονομάζεται σταθερά του ελατηρίου που μας δείχνει πόσα Νιούτον χρειάζονται για να προκληθεί επιμήκυνση 1 εκατοστό στο ελατήριο (είναι ο συντελεστής αναλογίας των δύο μεγεθών)
| Βάρος |
|
Βάρος ή Βαρυτική δύναμη της Γης είναι η ελκτική δύναμη που ασκεί η Γη σε οποιοδήποτε σώμα βρίσκεται στην επιφάνειά της ή κοντά σε αυτήν. Έχει τη διεύθυνση της ακτίνας της Γης στο σημείο που βρίσκεται το σώμα και φορά προς το κέντρο της Γης.
Οι βαρυτικές δυνάμεις είναι πάντα ελκτικές.
Η διεύθυνση της ακτίνας της Γης σε έναν τόπο ονομάζεται κατακόρυφος του τόπου.
Το βάρος μεταβάλλεται από τόπο σε τόπο και μειώνεται όσο απομακρυνόμαστε από το κέντρο της Γης.
Βαρυτικές δυνάμεις ασκούν όλα τα σώματα που έχουν μάζα σε κάθε άλλο σώμα με μάζα.
| Τριβή |
|
Τριβή είναι η δύναμη που ασκείται μεταξύ δύο σωμάτων που είναι σε επαφή και το ένα κινείται ή τείνει να κινηθεί ως προς το άλλο.
Σχεδιασμός δυνάμεων
- Επιλέγουμε το σώμα που μας ενδιαφέρει.
- Σχεδιάζουμε τις δυνάμεις που ασκούνται από απόσταση (Βάρος w)
- Σχεδιάζουμε τις δυνάμεις που ασκούνται από επαφή
- Επαφή με επιφάνεια:
- Αν είναι λεία η επιφάνεια σχεδιάζουμε μόνο την κάθετη δύναμη της επιφάνειας (FN ή N)
- Αν είναι τραχιά η επιφάνεια τότε σχεδιάζουμε και την Τριβή (Τ) με κατεύθυνση αντίθετη με τη κατεύθυνση κίνησης του σώματος
- Επαφή με νήμα ή σύρμα: Σχεδιάζουμε τη δύναμη που ασκεί το νήμα με διεύθυνση πάνω στο νήμα και φορά από το σώμα προς το νήμα
- Επαφή με ελατήριο: Σχεδιάζουμε τη δύναμη που ασκεί το ελατήριο με διεύθυνση πάνω στο ελατήριο και φορά τέτοια ώστε να επαναφέρει το ελατήριο στο φυσικό του μήκος (από το σώμα προς το ελατήριο αν είναι επιμηκυσμένο ή αντίθετα αν είναι συσπειρωμένο)
- Επαφή με επιφάνεια:
Σύνθεση δυνάμεων
Αν σε ένα σώμα ασκούνται πολλές δυνάμεις, τότε συνισταμένη δύναμη (Fολ), ονομάζεται η δύναμη που προκαλεί τα ίδια αποτελέσματα με το σύνολο των επιμέρους δυνάμεων (συνολική δύναμη).
1. Δυνάμεις με την ίδια διεύθυνση
- Αν δύο ή περισσότερες δυνάμεις με μέτρα F1, F2 κτλ έχουν ίδια διεύθυνση και φορά τότε η συνισταμένη τους (Fολ) έχει τη διεύθυνση και τη φορά των δυνάμεων και μέτρο:
![Rendered by QuickLaTeX.com \[ F_{o\lambda .} = F_1 + F_2\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-23aac08e47d669fc723e389d3824723d_l3.png)
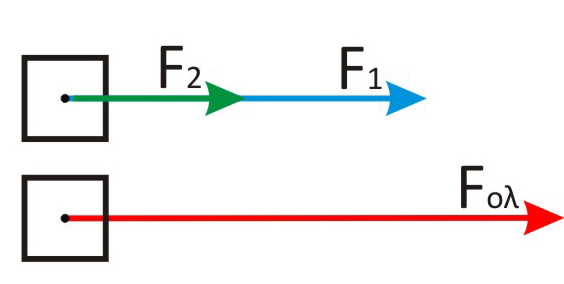
- Αν δύο δυνάμεις με μέτρα F1, F2 έχουν ίδια διεύθυνση αλλά αντίθετη φορά, τότε η συνισταμένη τους έχει τη διεύθυνση των δυνάμεων, τη φορά της μεγαλύτερης και μέτρο::
![Rendered by QuickLaTeX.com \[ F_{o\lambda .} = F_1 - F_2\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-d39ac82c211970473554a74f4f57b043_l3.png)
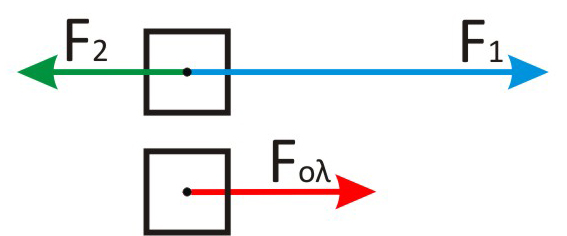
2. Δυνάμεις με διαφορετικές διευθύνσεις
- Για να συνθέσουμε δύο δυνάμεις με διαφορετικές διευθύνσεις, σχηματίζουμε το παραλληλόγραμμο που έχει για πλευρές τα διανύσματα που παριστάνουν τις δυνάμεις, και η διαγώνιος που περνά από την κοινή αρχή των διανυσμάτων, παριστάνει την συνισταμένη δύναμη:
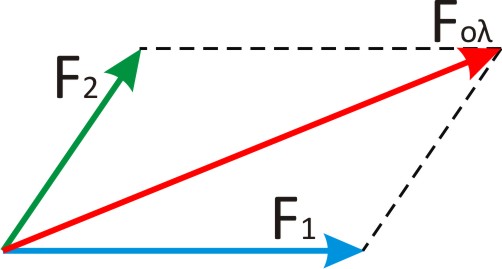
- Αν οι δυνάμεις είναι κάθετες μεταξύ τους, τότε μπορούμε να υπολογίσουμε και το μέτρο της διαγωνίου (από το Πυθαγόρειο Θεώρημα) κι έχουμε ότι:
\![Rendered by QuickLaTeX.com \[F^{2}_{o \lambda .} = F^{2}_1 + F^{2}_2\]](https://blogs.sch.gr/koutenp/wp-content/ql-cache/quicklatex.com-eb9791824ccd5f4e52acb2b4be550c59_l3.png)

ή αλλιώς:
![]()
Δύναμη και ισορροπία
1ος Νόμος του Νεύτωνα
Αν σε ένα σώμα δεν ασκούνται δυνάμεις ή η συνολική (συνισταμένη) δύναμη που ασκείται σε αυτό είναι μηδέν, τότε το σώμα είτε παραμένει ακίνητο είτε κινείται με σταθερή ταχύτητα (ευθύγραμμα ομαλά).
Αδράνεια είναι η τάση των σωμάτων να αντιστέκονται σε οποιαδήποτε μεταβολή της κινητικής τους κατάστασης (ταχύτητας).
Μέτρο της αδράνειας είναι η μάζα ενός σώματος.
Λέμε ότι ένα σώμα, που θεωρούμε υλικό σημείο, ισορροπεί όταν είναι ακίνητο ή κινείται με σταθερή ταχύτητα.
Δύναμη και μεταβολή της ταχύτητας
Όσο μεγαλύτερη είναι η δύναμη που ασκείται σε ένα σώμα, που έχει ορισμένη μάζα, τόσο γρηγορότερα μεταβάλλεται η ταχύτητά του.
Όσο μεγαλύτερη είναι η μάζα ενός σώματος, τόσο δυσκολότερα μπορεί να μεταβληθεί η ταχύτητά του.
Η μαθηματική σχέση που περιγράφει με ακρίβεια τις δύο παραπάνω προτάσεις διατυπώθηκε από τον Νεύτωνα και ονομάζεται 2ος Νόμος του Νεύτωνα.
| Διαφορές μάζας και βάρους | |
| Μάζα | Βάρος |
| Είναι το μέτρο της αδράνειας ενός σώματος. | Είναι η βαρυτική δύναμη που ασκεί η Γη σε ένα σώμα. |
| Είναι μονόμετρο μέγεθος | Είναι διανυσματικό μέγεθος |
| Παραμένει ίδια σε οποιοδήποτε σημείο του σύμπαντος. | Μεταβάλλεται από τόπο σε τόπο. |
| Έχει μονάδα μέτρησης το 1Kg | Έχει μονάδα μέτρησης το 1N |
| Συμβολίζεται με m | Συμβολίζεται με w |
| Είναι θεμελιώδες φυσικό μέγεθος | Είναι παράγωγο φυσικό μέγεθος |
| Μετριέται με ζυγό | Μετριέται με δυναμόμετρο |
Η μάζα (m) συνδέεται με το βάρος (w) ενός σώματος μέσω ενός μεγέθους που ονομάζεται επιτάχυνση της βαρύτητας (g) με τη σχέση:
![]()
Η τιμή του g στην επιφάνεια της Γης είναι περίπου 9,8 m/s.
Δύναμη και αλληλεπίδραση
3ος Νόμος του Νεύτωνα (Νόμος δράσης – αντίδρασης)
Όταν ένα σώμα ασκεί δύναμη σε ένα άλλο σώμα (δράση), τότε και το δεύτερο σώμα ασκεί δύναμη ίσου μέτρου και αντίθετης φοράς στο πρώτο (αντίδραση)
ή
Σε κάθε δράση αντιστοιχεί πάντα μία αντίθετη αντίδραση.
Οι δύο δυνάμεις δράση-αντίδραση, ασκούνται πάντα σε δύο διαφορετικά σώματα.
![]() Αυτή η εργασία έχει άδεια χρήσης Creative Commons -Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή4.0.
Αυτή η εργασία έχει άδεια χρήσης Creative Commons -Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή4.0.



 Άρθρα (RSS)
Άρθρα (RSS)