« 
 »
08 10 2013

Κινήσεις – Ταχύτητα

Αναρτήθηκε από Παναγιώτης Κουτεντάκης στο Φυσική Β' Γυμανσίου

Κίνηση

Η κίνηση είναι χαρακτηριστική ιδιότητα της ύλης κι εμφανίζεται από τους γαλαξίες μέχρι τα μικροσκοπικά σωματίδια.

Η κίνηση είναι μια έννοια σχετική, δηλαδή εξαρτάται από τον παρατηρητή (το σύστημα αναφοράς)

 

Θέση

(\vec{x} ) 

Για να προσδιορίσουμε τη θέση ενός σώματος σε μία διάσταση (ευθεία), επιλέγουμε ένα σημείο αναφοράς (Ο) και μία θετική φορά. Το μέτρο της θέσης  του σώματος θα ισούται με την απόσταση του σώματος από το σημείο αναφοράς ενώ η αλγεβρική της τιμή θα έχει θετικό πρόσημο (+) αν το σώμα βρίσκεται προς τη θετική φορά σε σχέση με το σημείο αναφοράς, ενώ αρνητικό πρόσημο (-) στην αντίθετη περίπτωση.

Μονάδα μέτρησης της θέσης είναι το μέτρο (m).

Ένα σώμα θα λέμε ότι κινείται όταν αλλάζει θέση.

 

Μετατόπιση 

(\Delta \vec{x}) 

Η μετατόπιση είναι η μεταβολή της θέσης  δηλαδή η διαφορά της αρχικής θέσης του σώματός από την τελική του θέση.

    \[\Delta \vec{x} = \vec{x}_2 - \vec{x}_1\]

Μονάδα μέτρησης της μετατόπισης είναι το μέτρο (m).

 

Προσομοίωση Μετατόπισης  από τον συνάδελφο Ηλία Σιτσανλή!

 

Χρονική στιγμή

 (t) 

Χρονική στιγμή είναι η ένδειξη ενός χρονομέτρου.

Μονάδα μέτρησης της χρονικής στιγμής είναι το δευτερόλεπτο (s).

 

 

 

Χρονική διάρκεια ή χρονικό διάστημα

(\Delta t) 

Χρονική διάρκεια ή χρονικό διάστημα ονομάζουμε το χρόνο μεταξύ δύο χρονικών στιγμών.  Δηλαδή :

    \[ \Delta t = t_2 - t_1\]

Μονάδα μέτρησης της χρονικής διάρκειας είναι το δευτερόλεπτο (s).

 

 

Μέση Ταχύτητα

(\upsilon_{\mu}) 

Η μέση ταχύτητα είναι μονόμετρο φυσικό μέγεθος και ορίζεται ως το συνολικό διάστημα που έχει διανύσει ένα σώμα προς το αντίστοιχο χρόνικό διάστημα. Δηλαδή:

    \begin{align*} μ\acute{ε}ση\hspace{2mm} ταχ\acute{υ}τητα &= \frac{ συνολικ\acute{o} \hspace{2mm} δι\acute{α}στημα}{συνολικ\acute{o}ς \hspace{2mm} χρ\acute{o}νος}\\ & \\ υ_{μ} &= \frac{s}{ t} \end{align*}

 

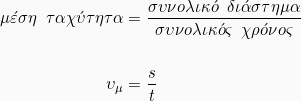
Μονάδα μέτρησης της μέσης ταχύτητας είναι το μέτρο ανά δευτερόλεπτο (m/s).

 

Στιγμιαία Ταχύτητα

Η στιγμιαία ταχύτητα είναι η ταχύτητα που έχει ένα σώμα μία συγκεκριμένη χρονική στιγμή, είναι δηλαδή η ταχύτητα που δείχνει το ταχύμετρο (κοντέρ) ενός αυτοκινήτου κάθε χρονική στιγμή.

 

Τροχιά

Τροχιά ονομάζουμε το σύνολο των διαδοχικών θέσεων από τις οποίες περνάει ένα σώμα όταν κινείται.

Διάστημα (s)

Το διάστημα που έχει διανύσει ένα σώμα είναι στην ουσία το μήκος της τροχιάς του. Όταν το σώμα κινείται προς μία κατεύθυνση σε ευθεία γραμμή, το διάστημα ταυτίζεται με την μετατόπιση.

 

Προσομοίωση για την διαφορά Τροχιάς και Μετατόπισης από τον συνάδελφο Ηλία Σιτσανλή.

 

Παράδειγμα 1

Σώμα Α βρίσκεται τη χρονική στιγμή t1=3s στη θέση x1=7m ενώ τη χρονική στιγμή t2=8s βρίσκεται στη θέση x2=22m.

  1. Ποια είναι η μετατόπιση του σώματος και ποιο το διάστημα που διήνυσε;;
  2. Ποια η χρονική διάρκεια της κίνησης;
  3. Ποια η μέση ταχύτητα του σώματος σε m/s αλλά και σε km/h;

 

Λύση

  1. Η μετατόπιση του σώματος θα είναι:

        \begin{align*} Δx &= x_{τελ.}-x_{αρχ.} \Rightarrow\\ Δx &= x_2 - x_1 \Rightarrow\\ Δx &= 22m - 7m \Rightarrow\\ Δx &= 15m \end{align*}

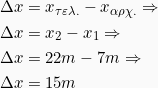
    Επειδή το σώμα δεν αλλάζει κατεύθυνση κατά την κίνησή του το διάστημα που διανύει θα είναι το ίδιο με την μετατόπισή του, δηλαδή:

        \[ s = Δx = 15m \]

  2. Η χρονική διάρκεια της κίνησης του σώματος θα είναι:

        \begin{align*} Δt &= t_{τελ.}-t_{αρχ.} \Rightarrow\\ Δt &= t_2 - t_1 \Rightarrow\\ Δt &= 8s - 3s \Rightarrow\\ Δt &= 5s \end{align*}

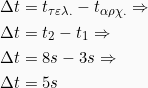
  3. Η μέση ταχύτητα του σώματος θα είναι:

        \begin{align*} υ_μ &= \frac{s}{Δt} \Rightarrow\\ υ_μ &= \frac{15m}{5s} \Rightarrow\\ υ_μ &= 3m/s \end{align*}

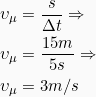
    Για να μετατρέψουμε την ταχύτητα σε km/h αρκεί να την πολλαπλασάσουμε με το 3,6 άρα:

        \[υ_μ = 3\cdot 3,6 = 10,8km/h \]

Παράδειγμα 2

Ένας δρομέας τρέχει τα 400m (έναν κύκλο στο στάδιο) σε 50s.

  1. Ποια η μετατόπιση του δρομέα και ποιο το διάστημα που διήνυσε;
  2. Ποια η μέση ταχύτητα του δρομέα;
  3. Πόσο χρόνο θα χρειαστεί ο δρομέας να διανύσει μία απόσταση 2km αν τρέχει συνεχώς με την μέση ταχύτητά του;
  4. Πόση απόσταση θα διανύσει ο δρομέας αν κινείται με την μέση ταχύτητά του για 10 λεπτά;

 

Λύση

  1. Επειδή ο δρομέας κάνει ένα κύκλο στο στάδιο και επιστρέφει στην αρχική του θέση, η μετατόπισή του είναι μηδέν (Δx=0m)! Όμως το συνολικό διάστημα που έχει διανύσει θα είναι s=400m.
  2. Η μέση ταχύτητα του δρομέα θα είναι:

        \begin{align*} υ_μ &= \frac{s}{t} \Rightarrow\\ υ_μ &= \frac{400m}{50s} \Rightarrow\\ υ_μ &= 8m/s\\ \end{align*}

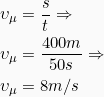
    ή σε km/h

        \[ υ_μ = 8\cdot3,6 = 28,8km/h \]

  3. Ο χρόνος που ια χρειαστεί ο δρομέας να διανύσει 2km = 2.000m θα είναι:

        \begin{align*} t &= \frac{s}{υ_μ} \Rightarrow\\ t &= \frac{2.000m}{8m/s} \Rightarrow\\ t &= 250s\\ \end{align*}

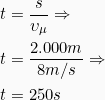
    ή αλλιώς 4 λεπτά και 10 δευτερόλεπτα.

  4.  Η απόσταση που θα διανύσει ο δρομέας σε 10λεπτά = 600s θα είναι:

        \begin{align*} s &= υ_μ \cdot t \Rightarrow\\ s &= 8m/s \cdot 600s\Rightarrow\\ s &= 4.800m\\ \end{align*}

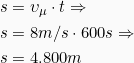
    ή αλλιώς 4,8km.

 

CC BY-NC-SA 4.0 Αυτή η εργασία έχει άδεια χρήσης Creative Commons -Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή4.0.

Το άρθρο δημοσιεύτηκε Τρίτη 8 Οκτωβρίου 2013 στις 18:51 στην κατηγορία Φυσική Β' Γυμανσίου. Μπορείς να παρακολουθείς τα σχόλια χρησιμοποιώντας το RSS 2.0 feed. Τα σχόλια και τα pings δεν επιτρέπονται.

Τα σχόλια είναι κλειστά.
Αλλαγή μεγέθους γραμματοσειράς
Αντίθεση
Accessibility by WAH
Μετάβαση σε γραμμή εργαλείων