»
15 09 2012

Φυσικά Μεγέθη – Ρυθμός Μεταβολής – Γραφικές Παραστάσεις

Αναρτήθηκε από Παναγιώτης Κουτεντάκης στο Φυσική Α' Λυκείου

Εισαγωγή

Φυσική είναι η επιστήμη η οποία περιγράφει και προσπαθεί να ερμηνεύσει τα Φυσικά Φαινόμενα.

Φυσικό Μέγεθος είναι μία ιδιότητα ενός σώματος ή μία έννοια που δημιουργούμε ώστε να περιγράψουμε και να ερμηνεύσουμε ένα φυσικό φαινόμενο  και την οποία μπορούμε να μετρήσουμε με ακρίβεια.

 

Κατηγορίες Φυσικών Μεγεθών

  1. Μονόμετρο: Το φυσικό μέγεθος που για να το προσδιορίσουμε πλήρως χρειαζόμαστε μόνο την αριθμιτική του τιμή (το μέτρο και τη μονάδα μέτρησής του).
  2. Διανυσματικό: Το φυσικό μέγεθος που για να το προσδιορίσουμε πλήρως χρειαζόμαστε:
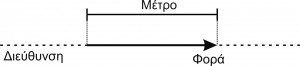
    1. Μέτρο: Ο θετρικός αριθμός, ο οποίος μας δείχνει πόσο μεγάλο είναι το φυσικό μέγεθος.
    2. Διεύθυνση: Η ευθεία (και κάθε παράλληλη αυτής) πάνω στην οποία «βρίσκεται» το φυσικό μέγεθος.
    3. Φορά: Το προς τα πού «πηγαίνει» το φυσκό μέγεθος.

Η Διεύθυνση μαζί με τη Φορά ονομάζεται Κατεύθυνση του διανυσματικού μεγέθους.

Τα διανυσματικά μεγέθη μπορούμε να τα αναπαραστήσουμε με τη μορφή ενός βέλους.

Κάθετα ονομάζονται τα διανυσματικά φυσικά μεγέθη που έχουν τις διευθύνσεις τους κάθετες μεταξύ τους.

Συγγραμμικά ονομάζονται τα διανυσματικά φυσικά μεγέθη που έχουν την ίδια διεύθυνση.

Ομόρροπα ονομάζονται τα συγγραμμικά διανυσματικά φυσικά μεγέθη που έχουν την ίδια φορά.

Αντίρροπα ονομάζονται τα συγγραμμικά διανυσματικά φυσικά μεγέθη που έχουν την αντίθετη φορά.

Ίσα ονομάζονται τα ομόρροπα διανυσματικά φυσικά μεγέθη που έχουν ίσα μέτρα.

Μεταβολή και Ρυθμός Μεταβολής

Η μεταβολή (Δ) ενός φυσικού μεγέθους (Θ) ονομάζεται η διαφορά της τελικής τιμής του μεγέθους από την αρχική του.

Συμβολικά:

\Delta \Theta = \Theta_{\tau \epsilon \lambda .} - \Theta_{\alpha \rho \chi .}

 

Ο ρυθμός μεταβολής ενός φυσικού μεγέθους (Θ) ονομάζεται το πηλίκο της μεταβολής του φυσικού μεγέθους (ΔΘ) προς τη μεταβολή του χρόνου Δt.

Συμβολικά:

\frac{\Delta\Theta}{\Delta t} = \frac{\Theta_{\tau \epsilon \lambda .}- \Theta_{\alpha \rho \chi .}}{t_{\tau \epsilon \lambda .} - t_{\alpha \rho \chi .}}

Γραφικές Παραστάσεις

Αν η συνάρτηση είναι πρώτου βαθμού (y = αx+β) τότε η γραφική παράσταση είναι ευθεία γραμμή και για να τη σχεδιάσουμε χρειαζόμαστε μόνο δύο σημεία.

Η κλίση της γραφικής παράστασης είναι η εφαπτομένη της γωνίας που σχηματίζει η ευθεία με τον άξονα των x και μπορεί να υπολογιστεί από το πηλίκο  όπου (x1,y1) και (x2,y2) είναι οι συντεταγμένες δύο σημείων της ευθείας

Αν η συνάρτηση είναι τριώνυμο δευτέρου βαθμού (y = αx2 + βx + γ) τότε η γραφική παράσταση είναι παραβολή (καμπύλη).

Η κλίση της γραφικής παράστασης σε ένα σημείο Μ, είναι η εφαπτομένη της γωνίας που σχηματίζει η εφαπτόμενη της γραφικής παράστασης στο σημείο Μ με τον άξονα των x.

CC BY-NC-SA 4.0 Αυτή η εργασία έχει άδεια χρήσης Creative Commons -Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή4.0.

Το άρθρο δημοσιεύτηκε Σάββατο 15 Σεπτεμβρίου 2012 στις 15:12 στην κατηγορία Φυσική Α' Λυκείου. Μπορείς να παρακολουθείς τα σχόλια χρησιμοποιώντας το RSS 2.0 feed. Τα σχόλια και τα pings δεν επιτρέπονται.

Τα σχόλια είναι κλειστά.
Αλλαγή μεγέθους γραμματοσειράς
Αντίθεση
Accessibility by WAH
Μετάβαση σε γραμμή εργαλείων