1. Το ηλεκτρικό ρεύμα
Ηλεκτρικό ρεύμα ονομάζουμε την προσανατολισμένη κίνηση ηλεκτρικών φορτίων (ηλεκτρόνια στα υλικά που χρησιμοποιούμε).
Αγωγοί – Μονωτές – Ημιαγωγοί
Μέσα σε έναν αγωγό (χαλκός, σίδηρος, αλουμίνιο) είναι δυνατόν να κινηθούν φορτισμένα σωματίδια (ηλεκτρόνια) και τότε δημιουργείται ηλεκτρικό ρεύμα.
Στους μονωτές (ξύλο, γυαλί), δεν υπάρχουν πολλά ελεύθερα ηλεκτρόνια, με συνέπεια να μην μπορεί να υπάρξει κίνηση ηλεκτρονίων, άρα και ηλεκτρικό ρεύμα.
Υπάρχουν ωστόσο υλικά (πυρίτιο, γερμάνιο), που υπό ορισμένες συνθήκες συμπεριφέρονται ως αγωγοί ενώ υπό κάποιες άλλες ως μονωτές. Τα υλικά αυτά ονομάζονται ημιαγωγοί.
Για να προκαλέσουμε ηλεκτρικό ρεύμα (προσανατολισμένη κίνηση ηλεκτρονίων) χρειαζόμαστε μία ηλεκτρική πηγή. Κάθε ηλεκτρική πηγή έχει δύο αντίθετα ηλεκτρισμένες περιοχές, που τις ονομάζουμε ηλεκτρικούς πόλους.
Όταν συνδέουμε έναν αγωγό στους δύο πόλους της πηγής, τότε στο εσωτερικό του αγωγού, δημιουργείται ένα ηλεκτρικό πεδίο, οπότε τα ελεύθερα ηλεκτρόνια του αγωγού κινούνται υπό την επίδραση της δύναμης του πεδίου προς μία κατεύθυνση.
Ένταση ηλεκτρικού ρεύματος
Για να μπορούμε να προσδιορίσουμε πότε το ρεύμα είναι ισχυρό ή ασθενές, ορίζουμε ένα νέο φυσικό μέγεθος, την ένταση του ηλεκτρικού ρεύματος (Ι).
Ορίζουμε την ένταση (Ι) του ηλεκτρικού ρεύματος που διαρρέει έναν αγωγό ως το πηλίκο του φορτίου (q) που διέρχεται από μία διατομή του αγωγού σε ένα χρονικό διάστημα (t) προς το χρονικό διάστημα αυτό.
Σε μαθηματική μορφή:
![]()
Όπως γνωρίζουμε από τη Β’ Γυμνασίου, η ένταση του ηλεκτρικού ρεύματος είναι θεμελιώδες φυσικό μέγεθος και η μονάδα μέτρησής της, στο S.I., είναι το Αμπέρ (A).
Από τον ορισμό της έντασης μπορούμε να βγάλουμε τη σχέση που συνδέει το Αμπέρ με το Κουλόμπ.
![]()
Το όργανο με το οποίο μπορούμε να μετρήσουμε την ένταση του ηλεκτρικού ρεύματος ονομάζεται αμπερόμετρο.
Τα αμπερόμετρα συνδέονται πάντα σε σειρά, δηλαδή παρεμβάλλονται στο σημείο του αγωγού που θέλουμε να μετρήσουμε την ένταση, έτσι ώστε το ρεύμα να περνάει μέσα από αυτό.
Φορά του ηλεκτρικού ρεύματος
Όπως είπαμε, μέσα σε έναν αγωγό, κινούνται τα ηλεκτρόνια. Σε ένα σύρμα λοιπόν, τα ηλεκτρόνια μπορούν να κινηθούν και προς τις δύο κατευθύνσεις, ανάλογα με τον τρόπο που έχουμε συνδέσει το σύρμα στους πόλους της πηγής.
Η φορά κίνησης των ηλεκτρονίων, ονομάζεται πραγματική φορά του ηλεκτρικού ρεύματος.
Όμως για ιστορικούς λόγους, έχει επικρατήσει να θεωρούμε σαν φορά του ηλεκτρικού ρεύματος, την αντίθετη φορά από αυτή των ηλεκτρονίων, την οποία ονομάζουμε συμβατική φορά του ηλεκτρικού ρεύματος.
Αποτελέσματα του ηλεκτρικού ρεύματος
Χωρίζουμε τα φαινόμενα που μπορεί να προκαλέσει το ηλεκτρικό ρεύμα στις εξής κατηγορίες:
- Θερμικά
- Ηλεκτρομαγνητικά
- Χημικά
- Φωτεινά
2. Το ηλεκτρικό κύκλωμα
Ηλεκτρικό κύκλωμα ονομάζουμε κάθε διάταξη από κλειστούς αγώγιμους “δρόμους”, μέσω των οποίων μπορεί να διέλθει ηλεκτρικό ρεύμα.
Όταν σε ένα κύκλωμα τα ηλεκτρόνια κινούνται μέσα στους αγωγούς και την πηγή ακολουθώντας μία κλειστή διαδρομή λέμε ότι το κύκλωμα είναι κλειστό.
Αντίθετα αν αποσυνδεθεί ένα σύρμα από τον πόλο της πηγής και τα ηλεκτρόνια δεν μπορούν πλέον να κινηθούν, λέμε ότι το κύκλωμα είναι ανοιχτό.
Για να μετατρέπουμε ένα κύκλωμα από ανοιχτό σε κλειστό και αντίστροφα, χρησιμοποιούμε έναν διακόπτη.
Ηλεκτρική πηγή και ενέργεια
Ενέργεια του ηλεκτρικού ρεύματος ονομάζουμε την ενέργεια που μεταφέρεται από την πηγή στα ηλεκτρόνια (δηλαδή το έργο της δύναμης του ηλεκτρικού πεδίου).
Πηγή ηλεκτρικής ενέργειας ή ηλεκτρική πηγή ονομάζουμε κάθε συσκευή που μετατρέπει μία μορφή ενέργειας σε ηλεκτρική ενέργεια.
Διαφορά Δυναμικού ή Ηλεκτρική Τάση
Ηλεκτρική τάση ή διαφορά δυναμικού (Vπηγής) μεταξύ των πόλων μίας ηλεκτρικής πηγής ονομάζουμε το πηλίκο της ενέργειας (Εηλ.) που προσφέρει η πηγή σε ηλεκτρόνια συνολικού φορτίου (q) όταν περνάνε μέσα από αυτή προς το φορτίο αυτό.
Δηλαδή:
![]()
Άρα η ενέργεια που προσφέρει η πηγή στα ηλεκτρόνια, δίνεται από τη σχέση:
![]()
Η μονάδα μέτρησης της ηλεκτρικής τάσης στο S.I. είναι το Volt (Βολτ) (1V) που ορίζεται ως:
![]()
Τα ηλεκτρόνια, καθώς κινούνται μέσα στο κύκλωμα και διέρχονται από κάποιες συσκευές, χάνουν ενέργεια η οποία μετατρέπεται σε αυτές τις συσκευές σε άλλες μορφές (θερμική, κινητική, φωτεινή κτλ).
Οι συσκευές που μετατρέπουν την ηλεκτρική ενέργεια σε ενέργεια άλλης μορφής, ονομάζονται καταναλωτές.
Με παρόμοιο τρόπο λοιπόν, ορίζεται και η ηλεκτρική τάση ή διαφορά δυναμικού στα άκρα ενός καταναλωτή
Ηλεκτρική τάση ή διαφορά δυναμικού (V) μεταξύ των άκρων ενός καταναλωτή ονομάζουμε το πηλίκο της ενέργειας (Εηλ.) που μεταφέρουν στον καταναλωτή ηλεκτρόνια συνολικού φορτίου (q) όταν περνάνε μέσα από αυτόν προς το φορτίο αυτό.
Δηλαδή:
![]()
Τη διαφορά δυναμικού την μετράμε με ειδικά όργανα τα οποία ονομάζονται βολτόμετρα και συνδέονται παράλληλα με το στοιχείο στα άκρα του οποίου θέλουμε να μετρήσουμε την ηλεκτρική τάση .
- Η ηλεκτρική τάση στα άκρα ενός καταναλωτή είναι μηδέν όταν αυτός δεν διαρρέεται από ρεύμα.
- Η ηλεκτρική τάση στους πόλους μίας πηγής δεν είναι μηδέν, είτε αυτή διαρρέεται από ρεύμα είτε όχι.
Πρέπει να προσέχουμε ότι η ηλεκτρική πηγή δεν δίνει ηλεκτρόνια ούτε ηλεκτρικό ρεύμα στο κύκλωμα αλλά ενέργεια.
Πολλές φορές για να περιγράψουμε ένα ηλεκτρικό κύκλωμα χρησιμοποιούμε σχηματικά διαγράμματα κυκλωμάτων όπου τα στοιχεία του κυκλώματος απεικονίζονται με συγκεκριμένα σύμβολα, όπως φαίνεται στην παρακάτω φωτογραφία.
3. Ηλεκτρικά δίπολα
Ηλεκτρικά δίπολα ονομάζονται οι συσκευές που διαθέτουν δύο άκρα (πόλους) για να συνδεθούν με το ηλεκτρικό κύκλωμα.
Ηλεκτρική αντίσταση δίπολου (R) ονομάζουμε το πηλίκο της ηλεκτρικής τάσης (V) που που εφαρμόζεται στα άκρα του προς την ένταση του ρεύματος (Ι) που το διαρρέει.
Δηλαδή:
![]()
Μονάδα μέτρησης της ηλεκτρικής αντίστασης είναι το 1Ωμ (Ohm) για το οποίο ισχύει:
![]()
Η ηλεκτρική αντίσταση μετριέται με ειδικά όργανα τα οποία ονομάζονται ωμόμεμτρα.
Αντιστάτες
Η ηλεκτρική αντίσταση συνήθως μεταβάλλεται ανάλογα με την τάση που εφαρμόζεται στα άκρα ενός δίπολου.
Όμως υπάρχει μία κατηγορία δίπολων, που ονομάζονται αντιστάτες, στους οποίους η αντίσταση δεν εξαρτάται ούτε από την ηλεκτρική τάση (V) που εφαρμόζεται στα άκρα του ούτε από την ένταση του ηλεκτρικού ρεύματος (I) που τον διαρρέει.
Ένας αντιστάτης, λοιπόν, έχει σταθερή αντίσταση η οποία εξαρτάται μόνο από τη θερμοκρασία του και τα χαρακτηριστικά κατασκευής του.
Νόμος του Ωμ
Η ένταση του ρεύματος που διαρρέει έναν μεταλλικό αγωγό (αντιστάτη) είναι ανάλογη της τάσης που εφαρμόζεται στα άκρα του. Δηλαδή:
![]()
4. Σύνδεση αντιστατών
Όταν σε ένα κύκλωμα έχουμε περισσότερους από έναν αντιστάτες, λέμε ότι έχουμε ένα σύστημα αντιστατών. Η ισοδύναμη αντίσταση του συστήματος αυτών των αντιστατών ονομάζουμε την αντίσταση που αν την τοποθετήσουμε στη θέση του συστήματος προκαλεί το ίδιο αποτέλεσμα.
Σύνδεση αντιστατών σε σειρά
Δύο αντιστάτες συνδέονται σε σειρά όταν διαρρέονται από το ίδιο ρεύμα κι έχουν ένα κοινό άκρο. (Σχήμα 1)
Όταν δύο οι περισσότεροι αντιστάτες συνδέονται σε σειρά η ισοδύναμη αντίστασή τους ισούται με το άθροισμα των αντιστάσεών τους.
![]()
Η ισοδύναμη αντίσταση που προκύπτει είναι μεγαλύτερη και από την μεγαλύτερη αντίσταση.
![]()
Η τάση στα άκρα του συστήματος των αντιστατών ισούται με το άθροισμα των τάσεων στα άκρα κάθε αντιστάτη.
![]()
Παράλληλη σύνδεση αντιστατών
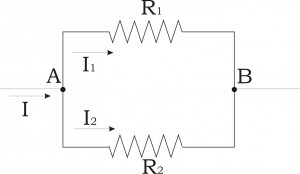
Δύο αντιστάτες είναι συνδεδεμένοι παράλληλα όταν έχουν τα ίδια άκρα, συνεπώς έχουν και την ίδια τάση στα άκρα τους. (Σχήμα 2)
Η ισοδύναμη αντίσταση του συστήματος των παράλληλων αντιστατών δίνεται από τη σχέση:
![]()
Αν έχουμε μόνο δύο αντιστάτες συνδεδεμένους παράλληλα τότε η παραπάνω σχέση μπορεί να λυθεί ως προς Rολ. Οπότε προκύπτει:
![]()
Η ισοδύναμη αντίσταση που προκύπτει είναι μικρότερη και από την μικρότερη αντίσταση.
![]()
Η ένταση του ρεύματος που εισέρχεται στο σύστημα των αντιστατών ισούται με την ένταση των ρευμάτων που διαρρέουν κάθε αντιστάτη. Δηλαδή:
![]()
Διαδικασία επίλυσης ασκήσεων ηλεκτρικών κυκλωμάτων
- Σχεδιάζουμε το κύκλωμα.
- Βάζουμε γράμματα στα άκρα των αντιστατών.
- Σχεδιάζουμε τις εντάσεις των ρευμάτων (Ι) που διαρρέουν τους αντιστάτες και την πηγή.
- Αναγνωρίζουμε τις αντιστάσεις που βρίσκονται σε σειρά ή παράλληλα και υπολογίζουμε την ισοδύναμη αντίσταση.
- Σχεδιάζουμε ξανά το κύκλωμα αντικαθιστώντας τις παραπάνω αντιστάσεις με την ισοδύναμή τους.
- Επαναλαμβάνουμε από το βήμα 4 μέχρι να καταλήξουμε σε ένα κύκλωμα με μία μόνο αντίσταση.
- Υπολογίζουμε τις εντάσεις των ρευμάτων (Ι) καθώς και τις τάσεις στα άκρα των αντιστατών (V) σε όλα τα κυκλώματα, ξεκινώντας από το τελευταίο και πηγαίνοντας προς τα πίσω.
Παραδείγματα επίλυσης ασκήσεων κυκλωμάτων
![]() Αυτή η εργασία έχει άδεια χρήσης Creative Commons -Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή4.0.
Αυτή η εργασία έχει άδεια χρήσης Creative Commons -Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή4.0.

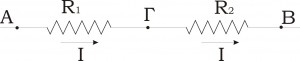
 Άρθρα (RSS)
Άρθρα (RSS)