Science & Education

17 01 2015

Παραδείγματα επίλυσης ασκήσεων κυκλωμάτων

Αναρτήθηκε από Παναγιώτης Κουτεντάκης στο Φυσική Γ' Γυμνασίου

Τύποι που θα χρειαστούμε

Ορισμός Έντασης:

(1) $\begin{equation*} I=\frac{q}{t} \end{equation*}$

Ορισμός Ηλεκτρικής Τάσης

(2) $\begin{equation*} V=\frac{E_{\eta \lambda .}}{q} \end{equation*}$

Ορισμός Αντίστασης

(3) $\begin{equation*} R = \frac{V}{I} \end{equation*}$

Νόμος του Ωμ

(4) $\begin{equation*} I = \frac{V}{R} \end{equation*}$

Πτώση Τάσης

(5) $\begin{equation*} V = I \cdot R \end{equation*}$

Σύνδεση αντιστατών σε σειρά

(6) $\begin{equation*} R_{o \lambda .} = R_1 + R_2 + \cdots \end{equation*}$

Σύνδεση αντιστατών παράλληαλα

(7) $\begin{equation*} \frac{1}{ R_{o \lambda .}} = \frac{1}{R_1} + \frac{1}{R_2} + \cdots \end{equation*}$

Σύνδεση αντιστατών παράλληλα (ισχύει ΜΟΝΟ για 2 αντιστάτες)

(8) $\begin{equation*} R_{o \lambda .} = \frac{R_1 \cdot R_2}{R_1 + R_2} \end{equation*}$

Άσκηση 1

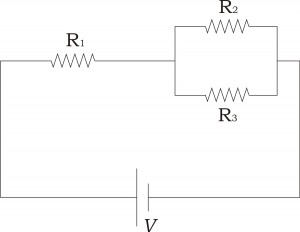
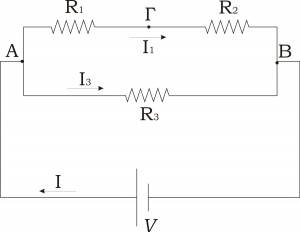
Στα άκρα πηγή τάσης 9V συνδέουμε τρεις αντιστάτες R₁, R₂ και R₃ όπως φαίνονται στο παρακάτω σχήμα (Σχήμα 1). Οι αντιστάτες έχουν αντίσταση 10Ω, 60Ω και 30Ω αντίστοιχα.

Σχήμα 1

Να σχεδιάσετε τις εντάσεις των ρευμάτων που διαρρέουν κάθε αντιστάτη.
Να υπολογίσετε την ένταση του ρεύματος που διαρρέει κάθε αντιστάτη.
Να υπολογίσετε την τάση στα άκρα κάθε αντιστάτη.

Λύση

Δεδομένα της άσκησης: V = 9V, R₁ = 10Ω, R₂ = 60Ω, R₃ = 30Ω

Βήματα 1, 2 και 3

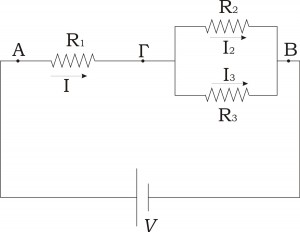
Σχεδιάζουμε το κύκλωμα (βήμα 1) τοποθετώντας γράμματα στα άκρα των αντιστατών (βήμα 2) και σχεδιάζουμε και τις εντάσεις των ρευμάτων (Ι) που διαρρέουν τους αντιστάτες (βήμα 3). Οπότε προκύπτει το παρακάτω σχήμα (Σχήμα 1α)

Σχήμα 1α

Βήμα 4

Παρατηρούμε ότι οι αντιστάτες R₂ και R₃ έχουν τα ίδια άκρα (Γ και Β) άρα είναι συνδεδεμένοι παράλληλα. Οπότε υπολογίζουμε την ισοδύναμη αντίσταση R_2,3 από τη σχέση (8) καθώς έχουμε μόνο 2 αντιστάτες παράλληλα:

$R_{2,3} = \frac{R_2 \cdot R_3}{R_2 + R_3} \Longleftrightarrow R_{2,3} = \frac{60\cdot 30}{60+30} \Longleftrightarrow R_{2,3} = \frac{1800}{90} \Longleftrightarrow R_{2,3} = 20\Omega$

Βήμα 5

Σχεδιάζουμε ξανά το κύκλωμα αντικαθιστώντας τους αντιστάτες R₂ και R₃ με τον ισοδύναμο R_2,3 οπότε προκύπτει το παρακάτω σχήμα (Σχήμα 1β):

Σχήμα 1β

Βήμα 6

Επαναλαμβάνουμε τα βήματα 4 και 5 καθώς το κύκλωμά μας δεν έχει μόνο έναν αντιστάτη.

Παρατηρούμε ότι οι αντιστάτες R₁ και R_2,3 έχουν ένα κοινό άκρο και διαρρέονται από το ίδιο ρεύμα, άρα είναι σε σειρά. Υπολογίζουμε λοιπόν την ισοδύναμη αντίσταση R_ολ. από τη σχέση (6):

$R_{o \lambda .} = R_1 + R_{2,3} \Longleftrightarrow R_{o \lambda .} = 10 + 20 \Longleftrightarrow R_{o \lambda .} = 30\Omega$

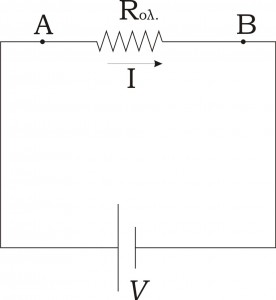
Και σχεδιάζουμε το νέο κύκλωμα όπου στη θέση των αντιστατών R₁ και R_2,3 βάζουμε τον ατνιστάτη R_ολ. οπότε προκύπτει το τελικό μας κύκλωμα (Σχήμα 1γ).

Σχήμα 1γ

Βήμα 7

Τώρα που καταλήξαμε σε κύκλωμα με έναν μόνο αντιστάτη, θα υπολογίσουμε όλα τα ρεύματα που διαρρέουν τους αντιστάτες κι όλες της τάσεις στα άκρα τους, ξεκινώντας από το τελευταίο κύκλωμα και πηγαίνοντας προς τα πίσω.

Σχήμα 1γ:

Η τάση V_ΑΒ είναι η ίδια με την τάση της πηγής, άρα:

$V_{AB} = 9V$

Η ένταση του ρεύματος I θα υπολογιστεί από την σχέση (4) όποτε έχουμε:

$I = \frac{V_{AB}}{R_{o \lambda .}} \Longleftrightarrow I = \frac{9}{30} \Longleftrightarrow I =0,3 A$

Σχήμα 1β:

Το ρεύμα που διαρρέει τους αντιστάτες είναι το ίδιο που υπολογίσαμε πριν, άρα το μόνο που πρέπει να υπολογίσουμε είναι οι τάσεις στα άκρα των αντιστατών δηλαδή V_AΓ και V_ΓΒ χρησιμοποιώντας τη σχέση (5):

$V_{A\Gamma} = I \cdot R_1 \Longleftrightarrow V_{A\Gamma} = 0,3 \cdot 10 \Longleftrightarrow V_{A\Gamma} = 3V$

$V_{\Gamma B} = I \cdot R_{2,3} \Longleftrightarrow V_{\Gamma B} = 0,3 \cdot 20 \Longleftrightarrow V_{\Gamma B} = 6V$

Φαίνεται να τα έχουμε υπολογίσει σωστά καθώς V_AB = V_AΓ + V_ΓΒ

Σχήμα 1α:

Οι τάσεις στα άκρα των αντιστατών είναι V_AΓ και V_ΓΒ που τις έχουμε ήδη υπολογίσει, οπότε το μόνο που μένει είναι να υπολογίσουμε τις εντάσεις Ι₂ και Ι₃ από τη σχέση (4):

$I_2 = \frac{V_{\Gamma B}}{R_2} \Longleftrightarrow I_2 = \frac{6}{60} \Longleftrightarrow I_2 = 0,1A$

$I_3 = \frac{V_{\Gamma B}}{R_3} \Longleftrightarrow I_3 = \frac{6}{30} \Longleftrightarrow I_2 = 0,2A$

Φαίνεται να τα έχουμε υπολογίσει σωστά καθώς Ι = Ι₂ + Ι₃

Τώρα κοιτώντας τι μας ζητάει η άσκηση απαντάμε τα ερωτήματα:

1. Έχουμε ήδη σχεδιάσει τις εντάσεις των ρευμάτων που διαρρέουν τους αντιστάτες στο Σχήμα 1α.

2. Έχουμε ήδη υπολογίσει τις εντάσεις των ρευμάτων που διαρρέουν τους αντιστάτες (Ι, Ι₂ και Ι₃).

3. Έχουμε ήδη υπολογίσει τις τάσεις στα άκρα των αντιστατών (V_ΑΓ και V_ΓΒ).

Άσκηση 2

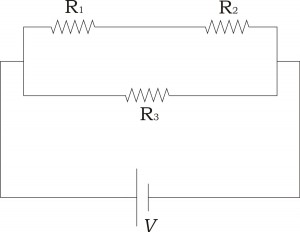
Στα άκρα πηγή τάσης 12V συνδέουμε τρεις αντιστάτες R₁, R₂ και R₃ όπως φαίνονται στο παρακάτω σχήμα (Σχήμα 2). Οι αντιστάτες έχουν αντίσταση 10Ω, 50Ω και 30Ω αντίστοιχα.

Σχήμα 2

Να σχεδιάσετε τις εντάσεις των ρευμάτων που διαρρέουν κάθε αντιστάτη.
Να υπολογίσετε την ένταση του ρεύματος που διαρρέει κάθε αντιστάτη.
Να υπολογίσετε την τάση στα άκρα κάθε αντιστάτη.

Λύση

Δεδομένα της άσκησης: V = 12V, R₁ = 10Ω, R₂ = 50Ω, R₃ = 30Ω

Η επίλυση αυτής της άσκησης θα γίνει συνοπτικά. Προσπαθήστε να εξηγήσετε μόνοι σας τα βήματα.

Βήματα 1, 2 και 3

Σχήμα 2α

Βήμα 4

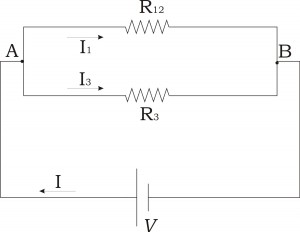
Οι R₁ και R₂ είναι σε σειρά:

$R_{1,2} = R_1 + R_2 \Longleftrightarrow R_{1,2} = 10 + 50 \Longleftrightarrow R_{1,2} = 60\Omega$

Βήμα 5

Σχήμα 2β

Βήμα 6

Οι R_1,2 και R₃ είναι παράλληλα:

$R_{o \lambda .} = \frac{R_{1,2} \cdot R_3}{R_{1,2}+R_3} \Longleftrightarrow R_{o \lambda .} = \frac{60 \cdot 30}{60+30} \Longleftrightarrow R_{o \lambda .} = \frac{1800}{90} \Longleftrightarrow R_{o \lambda .} = 20\Omega$

Σχήμα 2γ

Βήμα 7

Σχήμα 2γ:

$V_{AB} = 9V$

$I = \frac{V_{AB}}{R_{o \lambda .}} \Longleftrightarrow I = \frac{12}{20} \Longleftrightarrow I =0,6 A$

Σχήμα 2β:

$I_1 = \frac{V_{AB}}{R_{1,2}} \Longleftrightarrow I_1 = \frac{12}{60} \Longleftrightarrow I_1 = 0,2A$

$I_3 = \frac{V_{AB}}{R_3} \Longleftrightarrow I_3 = \frac{12}{30} \Longleftrightarrow I_2 = 0,4A$

Σχήμα 2α:

$V_{A\Gamma} = I_1 \cdot R_1 \Longleftrightarrow V_{A\Gamma} = 0,2 \cdot 10 \Longleftrightarrow V_{A\Gamma} = 2V$

$V_{\Gamma B} = I_1 \cdot R_2 \Longleftrightarrow V_{\Gamma B} = 0,2 \cdot 50 \Longleftrightarrow V_{\Gamma B} = 10V$

Τώρα κοιτώντας τι μας ζητάει η άσκηση απαντάμε τα ερωτήματα:

1. Έχουμε ήδη σχεδιάσει τις εντάσεις των ρευμάτων που διαρρέουν τους αντιστάτες στο Σχήμα 2α.

2. Έχουμε ήδη υπολογίσει τις εντάσεις των ρευμάτων που διαρρέουν τους αντιστάτες (Ι₁ και Ι₃).

3. Έχουμε ήδη υπολογίσει τις τάσεις στα άκρα των αντιστατών (V_AB, V_ΑΓ και V_ΓΒ).

Αυτή η εργασία έχει άδεια χρήσης Creative Commons -Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή4.0.

Το άρθρο δημοσιεύτηκε Σάββατο 17 Ιανουαρίου 2015 στις 19:12 στην κατηγορία Φυσική Γ' Γυμνασίου. Μπορείς να παρακολουθείς τα σχόλια χρησιμοποιώντας το RSS 2.0 feed. Τα σχόλια και τα pings δεν επιτρέπονται.

Τα σχόλια είναι κλειστά.

Open your mind…

Παραδείγματα επίλυσης ασκήσεων κυκλωμάτων

Σελίδες