Αξιοποίηση χειραπτικών και ψηφιακών εργαλείων στη διδασκαλία του Πυθαγορείου Θεωρήματος
Αν και η αρχική ανακάλυψη του Πυθαγορείου θεωρήματος είναι ασαφής, γνωρίζουμε ότι ήταν γνωστό πολύ πριν από τον Ευκλείδη και τον Πυθαγόρα, όπως φαίνεται σε αρχαία κείμενα από τη Βαβυλώνα, την Ινδία και την Κίνα. Εντούτοις, τα κείμενα αυτά δεν παρέχουν αποδείξεις για το θεώρημα, παρουσιάζοντας το ως έναν υπολογιστικό κανόνα ή πρακτικό εργαλείο χωρίς εξήγηση.
Η απόδειξη του Πυθαγορείου θεωρήματος εμφανίζεται για πρώτη φορά στο έργο του Ευκλείδη, στα «Στοιχεία». Αποδίδεται παραδοσιακά στον Πυθαγόρα, ωστόσο η πραγματική ανάπτυξή της φαίνεται να ξεκίνησε στην αρχαία Ελλάδα και χρειάστηκε αρκετός χρόνος για να ολοκληρωθεί.
Το Πυθαγόρειο θεώρημα είναι ένα από τα θεωρήματα που τράβηξε, περισσότερο ίσως από κάθε άλλο, το ενδιαφέρον των ανθρώπων. Υπάρχουν περισσότερες από 520 διαφορετικές αποδείξεις του.
Τέλος, για τους ιστορικούς το πόσο κοντά πλησίασε ένας λαός στην απόδειξη του Πυθαγορείου Θεωρήματος είναι ένας τρόπος για να δείξουν πόσο προχωρημένος ήταν ο πολιτισμός του.
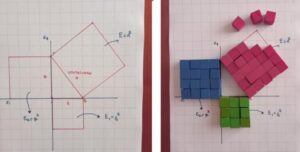
Στα πλαίσια του μαθήματος των Μαθηματικών στη Β’ Γυμνασίου, οι μαθητές έρχονται για πρώτη φορά σε επαφή με το Πυθαγόρειο Θεώρημα και το αντίστροφό του. Η μέθοδος διδασκαλίας που ακολουθήθηκε εστίασε στη χρήση χειραπτικών υλικών και του λογισμικού Geogebra, προκειμένου οι μαθητές ομαδοσυνεργατικά να ανακαλύψουν το θεώρημα. Τόσο μέσα στην τάξη, όσο και στο σπίτι τους δόθηκε η ευκαιρία να πειραματιστούν με απλά υλικά, να παίξουν και να δημιουργήσουν. Η χρήση χειραπτικών εργαλείων συνήθως δίνει στους μαθητές τη δυνατότητα σύνδεσης της άτυπης με την τυπική γνώση. Τα ψηφιακά εργαλεία ευνοούν τον πειραματισμό, την επανάληψη και τη διερεύνηση.
Εικόνα 1: «Απόδειξη» θεωρήματος με χειραπτικά μέσα
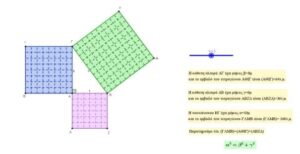
Εικόνα 2: «Απόδειξη» θεωρήματος με το λογισμικό
Εικόνα 3: Αυτοσχέδια αρπεδόνη από γλωσσοπίεστρα για τον σχηματισμό ορθών γωνιών
Εικόνα 4: Δραστηριότητα από την καθημερινότητα με τη χρήση του λογισμικού Geogebra
Οι μαθητές είχαν επίσης την ευκαιρία να «αποδείξουν» το Πυθαγόρειο θεώρημα σχεδιάζοντας και παίζοντας με ένα πυθαγόρειο puzzle-γρίφο. Αξιοποιώντας απλά υλικά, όπως χαρτόνι, ορισμένοι μαθητές σχεδίασαν σύμφωνα με τις οδηγίες που τους δόθηκαν, ένα puzzle που αποτελείται από επτά κομμάτια. Τοποθετώντας κατάλληλα γύρω από το μεγαλύτερο τρίγωνο τα υπόλοιπα κομμάτια του puzzle, οδηγήθηκαν σε μια εικόνα, όπως αυτή της αρχικής εφαρμογής (Εικόνα 1). Αναδιατάσσοντας τα ίδια κομμάτια, παρατήρησαν ότι τα μικρότερα μέρη του μπορούν να σχηματίσουν ένα τετράγωνο ίδιο με το μεγαλύτερο τετράγωνο της ιδιοκατασκευής.
Εικόνα 5: Ιδιοκατασκευή μαθήτριας
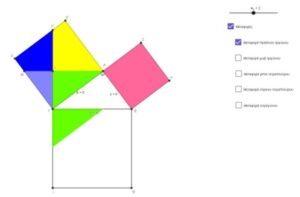
Οι μαθητές που δεν κατάφεραν να φτάσουν στο προηγούμενο συμπέρασμα, μπόρεσαν να δουν τη λύση του γρίφου, μέσω εφαρμογής που έχει δημιουργηθεί για αυτούς, στο περιβάλλον του λογισμικού Geogebra.
Εικόνα 6: Πυθαγόρειο puzzle σε ψηφιακό περιβάλλον
Video ιδιοκατασκευής
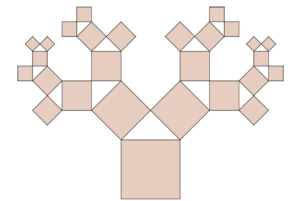
Τέλος, δύο μαθήτριες σχεδίασαν ένα Πυθαγόρειο δέντρο, το οποίο πλέον κοσμεί την αίθουσά τους. Τα πυθαγόρεια δέντρα αποτελούν έναν τύπο φράκταλ, που επινόησε ο Ολλανδός καθηγητής μαθηματικών Albert E. Bosman το 1942. Για να σχηματίσουμε πυθαγόρεια δέντρα σχεδιάζουμε τριάδες τετραγώνων που περικλείουν κάθε φορά ένα ορθογώνιο τρίγωνο, δηλαδή έχουμε μια απεικόνιση ίδια με αυτή του πυθαγορείου θεωρήματος, που διδάχτηκαν οι μαθητές στην πρώτη επαφή τους με το πυθαγόρειο θεώρημα, όταν αξιοποίησαν τους κύβους. Εφαρμόζοντας αναδρομικά αυτόν τον κανόνα κατασκευής, δημιουργούμε ένα φράκταλ που, στο τέλος, μοιάζει με το σχήμα ενός δέντρου.
Εικόνα 7: Πυθαγόρειο δέντρο
Η κατασκευή ενός τέτοιου δέντρου απαιτεί χρόνο και προσοχή, συμβάλει όμως στην ανάπτυξη και ανάδειξη σχεδιαστικών δεξιοτήτων των μαθητών.
Εικόνα 8: Πυθαγόρειο δέντρο σχεδιασμένο από μαθήτριες του σχολείου