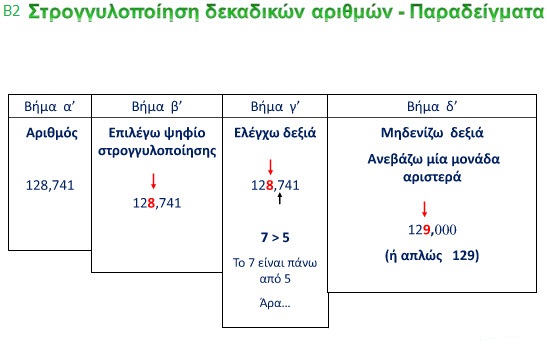
ΔΙΑΙΡΕΣΗ ΑΚΕΡΑΙΟΥ ΜΕ ΑΚΕΡΑΙΟ ΜΕ ΠΗΛΙΚΟ ΔΕΚΑΔΙΚΟ ΑΡΙΘΜΟ
Yπολογίζω το αποτέλεσμα μιας διαίρεσης με μεγαλύτερη ακρίβεια ως εξής:
-
Αν αφήνει υπόλοιπο, βάζω υποδιαστολή στο πηλίκο, προσθέτω το ψηφίο 0 στο υπόλοιπο μετατρέποντάς το σε δέκατα, και συνεχίζω τη διαίρεση.
-
Αν ο διαιρέτης δε χωράει στο διαιρετέο, βάζω 0 στο πηλίκο και υποδιαστολή, μετατρέπω το διαιρετέο σε δέκατα και συνεχίζω τη διαίρεση.