Το λήμμα Γεωμετρία : Σχήμα και σχέδιο είναι απόσπασμα
του άρθρου
Πατσιομίτου, Σ. (2009). Γνωστικές αλληλεπιδράσεις στις κατασκευές μέσω του λογισμικού δυναμικής γεωμετρίας Geometer’s Sketchpad. Πρακτικά 1ου Εκπαιδευτικού Συνεδρίου ΕΤΠΕ με τίτλο «Ένταξη και χρήση των ΤΠΕ στην Εκπαιδευτική διαδικασία», σσ. 129-134. Βόλος, 24-26 Απριλίου. http://www.etpe.gr/custom/pdf/etpe1440.pdf
…………………………………………………………………………………………………………………………………….
Η διαφορά μεταξύ του σχήματος-σχεδίου διατυπώθηκε από πολλούς ερευνητές. «Η Dina van Hiele αναφέρεται σε ‘σχέδια και κατασκευές’ που οι μαθητές δημιουργούν. Για τον Parzysz (1988), ένα σχέδιο είναι «η αναπαράσταση ενός γεωμετρικού αντικειμένου» ενώ το σχήμα είναι «η έννοια που καθορίζει αυτό το θεωρητικό αντικείμενο». Η Laborde (1993), επίσης, καθιστά σαφή τη διάκριση μεταξύ σχεδίου-σχήματος επισημαίνοντας ότι: «το σχέδιο αναφέρεται στην υλική οντότητα. Το σχήμα περιλαμβάνει το σύνολο των αναπαραστάσεων και των διαγραμμάτων που αναφέρονται στο θεωρητικό αντικείμενο. Το σχήμα τότε συνδέει το σχέδιο με το αφηρημένο γεωμετρικό αντικείμενο» (Hollebrands, 2007, p.167)» (Πατσιομίτου, 2012, 2020, σελ. 60-61).
Με το υλικό αντικείμενο «σχέδιο» και το θεωρητικό αντικείμενο «σχήμα», η γεωμετρία μας παρέχει δύο συμπληρωματικές έννοιες, τις οποίες μπορούμε να χρησιμοποιήσουμε. Για παράδειγμα, η αιτιολόγηση ότι δυο τρίγωνα είναι ίσα, αφ’ ενός αναφέρεται στα αφηρημένα νοητικά αντικείμενα, όπως είναι οι έννοιες της γωνίας, πλευράς, τρίγωνου, αλλά και στις σχηματικές πληροφορίες ή τις σχηματικά αντιπροσωπευόμενες διαδικασίες, που προέρχονται από τις οπτικές εικόνες που μπορεί να προέλθουν από την ταύτιση των δύο γωνιών και των πλευρών που οριοθετούν τη γωνία. Επομένως, αφού ενδιαφερόμαστε για την ανάπτυξη του γεωμετρικού συλλογισμού-αιτιολόγησης θα πρέπει να ασχοληθούμε με την αλληλεπίδραση μεταξύ των δύο πτυχών: των σχηματικών και των εννοιολογικών (Mariotti, 1992, 1996). Αυτός ο προσδιορισμός είναι κοντά στην σχηματική έννοια (figural concept) όπως διατυπώνεται από τον Fishbein (1993) σύμφωνα με τον οποίο μια γεωμετρική έννοια περιλαμβάνει δύο πραγματικά συνδεδεμένες συνιστώσες ως δύο πλευρές ενός νομίσματος, την σχηματική (figural) και την εννοιολογική (conceptual). «Ο Fischbein, θεωρεί ότι η έννοια του σχήματος (figure) δε μπορεί να προσδιοριστεί με σαφήνεια. Ένα σχήμα είναι μία δομική μορφή, όπως θεωρείται η έννοια της «μορφής» στη θεωρία “gestalt”. Ο Fischbein (1993, p.149) ορίζει
- το γεωμετρικό σχήμα (geometrical figure) ως μία νοητική εικόνα, οι ιδιότητες της οποίας είναι απολύτως ελεγχόμενες από έναν ορισμό, και ως νοητική εικόνα ενός γεωμετρικού σχήματος θεωρεί τη (νοητική) αναπαράσταση του υλικού του μοντέλου. Η νοητική εικόνα (mental image) είναι αποτέλεσμα μίας αισθητήριας (sensorial) αναπαράστασης ενός αντικειμένου ή ενός φαινομένου» (Fischbein, 1993, p.139).
- το σχέδιο (drawing), ως το υλικό μέρος ενός σχήματος» (Πατσιομίτου, 2020, σελ. 132).
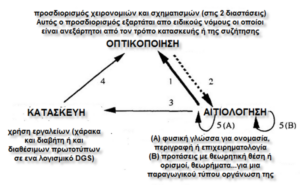
Είναι προφανές ότι αυτό που μας ενδιαφέρει και επιδιώκουμε είναι οι μαθητές μας να κατασκευάζουν ένα γεωμετρικό σχήμα και όχι ένα γεωμετρικό σχέδιο. Ακόμα, να έχουν τη δυνατότητα να αιτιολογήσουν με λεκτικές διατυπώσεις που συνδέουν τις πληροφορίες μεταξύ τους, με καταλλήλους ορισμούς ή θεωρήματα. Να συνδέσουν δηλαδή με τον τρόπο αυτό σημαντικές γνωστικές διαδικασίες, με στόχο οι ενέργειες τους στα μαθηματικά αντικείμενα που αναπαριστάνουν — ευθείες, κύκλους, τρίγωνα κ.λπ.– να σχετίζονται με την απόδοση της νοητικής εικόνας που έχουν σχηματίσει για τα γεωμετρικά αντικείμενα που οπτικοποιούν και την επεξήγηση τους. Να συνδέσουν δηλαδή λειτουργίες οπτικοποίησης (Visualization), κατασκευής (Construction) και αιτιολόγησης (Reasoning) (π.χ. Duval, 1998) λειτουργίες που παρά το γεγονός ότι είναι ανεξάρτητες, συνδέονται στενά μεταξύ τους με αποτέλεσμα να έχουν ή όχι επαρκείς γνώσεις στη Γεωμετρία.
«Ο Duval (1998, p.38) υποστηρίζει ότι ο γεωμετρικός συλλογισμός περιλαμβάνει τρία είδη γνωστικών λειτουργιών. Αυτές οι γνωστικές λειτουργίες είναι (Σχήμα 3.1.):
- οπτικοποίηση (visualization): είναι η γνωστική λειτουργία που αφορά τις οπτικές αναπαραστάσεις μίας γεωμετρικής διατύπωσης (π.χ. η απόδοση του νοήματος της εκφώνησης ενός προβλήματος με κάποιο αντίστοιχο σχήμα) ή η ευρετική διερεύνηση μίας σύνθετης γεωμετρικής κατάστασης προβλήματος, στο οποίο υπεισέρχονται νοητικές διαδικασίες για την επίλυσή του. Η οπτικοποίηση δεν εξαρτάται από τη διαδικασία κατασκευής και δεν βοηθά πάντα τους μαθητές να αιτιολογήσουν.
Σχήμα: Γνωστικές αλληλεπιδράσεις που εμπλέκονται σε μία γεωμετρική δραστηριότητα (Duval, 1998, p. 38, προσαρμογή ό.α. στο Πατσιομίτου, 2020, σελ. 130)
- κατασκευή (construction): είναι η γνωστική λειτουργία που αφορά τις κατασκευές με χρήση εργαλείων παραδοσιακών ή δυναμικών (π.χ. με χρήση γεωμετρικών οργάνων όπως είναι ο κανόνας και διαβήτης ή με χρήση εργαλείων και πρωτογενών αντικειμένων (primitives) ενός λογισμικού δυναμικής γεωμετρίας).
- αιτιολόγηση (reasoning): είναι η γνωστική λειτουργία που αφορά τις λεκτικές διαδικασίες οι οποίες στοχεύουν να επεξηγήσουν, να αιτιολογήσουν ή να αποδείξουν μία πρόταση» (Πατσιομίτου, 2020, σελ. 129-130).
Τα προβλήματα κατασκευής γεωμετρικών σχημάτων, αποτελούν τον πυρήνα των δραστηριοτήτων που προτείνονται στους μαθητές. Παρά τον προφανή πρακτικό στόχο, δηλ. το σχήμα που πρέπει να πραγματοποιηθεί σε ένα στατικό ή δυναμικό μέσο, οι γεωμετρικές κατασκευές έχουν σαφή θεωρητικό στόχο. Ο κύριος στόχος είναι η ανάπτυξη της έννοιας «της κατασκευής», ως θεωρητικής διαδικασίας και ως αποτέλεσμα της διαδικασίας η σύνθεση των ιδιοτήτων του σχήματος. Έχω επιλέξει να παρουσιάσω την κατασκευή της μεσοκαθέτου τμήματος και τις συνδέσεις που προκύπτουν μεταξύ χωρογραφικού και θεωρητικού πεδίου, κατά την αλληλεπίδραση με συνδυασμούς εργαλείων.
…………………………………………………………………………………………………………………………………..
Αναφορά στη μονογραφία
Πατσιομίτου, Σ. (2020b). Διδακτική, Διδασκαλία και Αξιολόγηση των Μαθηματικών: Μαθησιακά μονοπάτια και Πρόγραμμα Σπουδών. Μονογραφία. Ανατολικός. ISBN: 978-618-5136-49-9. https://www.academia.edu/43702210/