Blaise Pascal – Βιογραφία

Ο Blaise Pascal (19 Ιουνίου 1623 – 19 Αυγούστου 1662) ήταν Γάλλος μαθηματικός, φυσικός, συγγραφέας και φιλόσοφος.
O Πασκάλ άρχισε να μελετά γεωμετρία σε ηλικία δώδεκα ετών. Ανακάλυψε μόνος του ότι το άθροισμα των γωνιών ενός τριγώνου ισούται με δύο ορθές γωνίες και όταν ο πατέρας του, Ετιέν, είδε τα επιτεύγματα του γιου του, εντυπωσιάστηκε τόσο ώστε να αποφασίσει να άρει την απόφασή του, και να επιτρέψει στο γιο τη μελέτη μαθηματικών κειμένων, αρχίζοντας με το κλασσικό έργο “Στοιχεία” του Ευκλείδη. Άρχισε επίσης να πηγαίνει, τον προφανώς χαρισματικό Μπλεζ στις συναντήσεις της Ακαδημίας του Μερσέν, μια από τις πολλές ημιεπίσημες ομάδες μαθηματικών και επιστημόνων στο Παρίσι, οι οποίες οδήγησαν στη ίδρυση της Βασιλικής Ακαδημίας Επιστημών το 1666. Στα 16 του χρόνια ανέπτυξε σε μια πραγματεία περί κωνικών τομών το θεώρημα που φέρει το όνομά του.
Από το 1641 και για περίπου 3 χρόνια εργάστηκε για την κατασκευή μιας αριθμομηχανής που μπορούσε να κάνει πρόσθεση και αφαίρεση που ονομάστηκε «Πασκαλίνα». Παρόλη την ενασχόλησή του, δεν πέτυχε ως επιχειρηματίας αριθμομηχανών: η μηχανή του δεν έκανε μεγάλες πωλήσεις και, τελικά, σταμάτησε να παράγεται. Το 1647 ανακάλυψε την Αρχή του Πασκάλ και τη χρήση τού βαρομέτρου για τη μέτρηση του υψομέτρου. Με την εργασία του Traité du triangle arithmétique, που δημοσιεύτηκε το 1654, έθεσε τις βάσεις για τη Συνδυαστική και το Λογισμό των Πιθανοτήτων. Επίσης μια από τις πιο γνωστές μαθηματικές μελέτες του είναι αυτό που ονομάζουμε “τρίγωνο του Πασκάλ” ή απλούστερα “αριθμητικό τρίγωνο”.
Ήταν στοχαστής και δημιούργησε πολλά αποφθέγματα όπως: “Άνθρωπος: η δόξα και η ντροπή του σύμπαντος.”
Το τρίγωνο του Πασκάλ
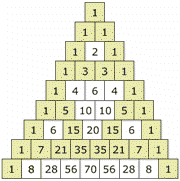
Στα μαθηματικά, το τρίγωνο του Πασκάλ είναι μία τριγωνική γεωμετρική διάταξη των δυωνυμικών συντελεστών. Ονομάστηκε έτσι προς τιμήν του μαθηματικού Μπλεζ Πασκάλ στο μεγαλύτερο μέρος του δυτικού κόσμου, παρόλο που άλλοι μαθηματικοί το είχαν μελετήσει αιώνες πριν στην Ινδία, την Περσία, την Κίνα και την Ιταλία.
Οι σειρές στο τρίγωνο του Πασκάλ αριθμούνται ξεκινώντας από την γραμμή 0, και οι αριθμοί κάθε σειράς είναι συνήθως σχετικοί με τις διπλανές τους. Μια απλή κατασκευή του τριγώνου γίνεται με τον ακόλουθο τρόπο. Στην σειρά 0 γράφεται μόνο ο αριθμός 1. Μετά, για την κατασκευή των στοιχείων των ακόλουθων σειρών προστίθεται ο αριθμός που βρίσκεται αμέσως από πάνω και αριστερά με τον αριθμό αμέσως από πάνω και δεξιά. Αν οποιοσδήποτε από τους αριθμούς δεξιά ή αριστερά δεν υπάρχει, υποκαθίσταται με μηδέν. Για παράδειγμα, ο πρώτος αριθμός της πρώτης γραμμής είναι 0 + 1 = 1, ενώ οι αριθμοί 1 και 3 της τρίτης σειρά προτίθενται ώστε να δώσουν τον αριθμό 4 της τέταρτης σειράς.

Ενδιαφέροντα μοτίβα
1) H πρώτη διαγώνιος περιλαμβάνει μόνο τον αριθμό 1. Η δεύτερη τους φυσικούς ξεκινώντας από το 1 με τη σειρά, ενώ η τρίτη τους τριγωνικούς αριθμούς* (η τέταρτη τους τετραγωνικού κλπ.)
2) Το αριστερό μέρος του τριγώνου είναι εντελώς συμμετρικό προς το δεξίο με άξονα συμμετρίας την μεσοκάθετο της κάτω πλευρά του πρώτου τετραγώνου. (εμφανίζονται δηλαδή οι ίδιοι αριθμοί στις αντίστοιχες θέσεις)

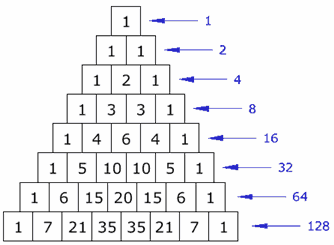
3) Τα αθροίσματα των αριθμών των οριζόντιων σειρών του τριγώνου δίνουν ως αποτέλεσμα τον αριθμό 2 υψωμένο στον αριθμό της σειράς (μην ξεχνάτε ότι η αρίθμηση ξεκινά από το 0).
4) Όπως παρατηρούμε οι αριθμοί που υπάρχουν σε κάθε σειρά δίνουν τα ψηφία του αριθμού 11 υψωμένο στον αριθμό της σειράς.
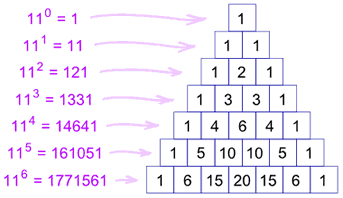
Παρατήρηση: Από το 115 και μετά που εμφανίζονται διψήφιοι αριθμοί ο τρόπος σχηματισμού είναι ο εξής:
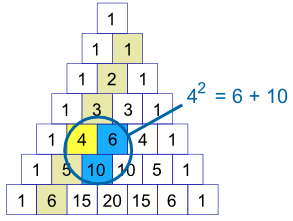
5) Το τετράγωνο των αριθμών της δεύτερης διαγωνίου είναι ίσο με το άθροισμα του αριθμού που βρίσκεται δεξιά τους και κάτω τους (δυο διαδοχικών αριθμών δηλαδή της τρίτης διαγωνίου με πρώτο αυτόν που βρίσκεται ακριβώς δεξιά)
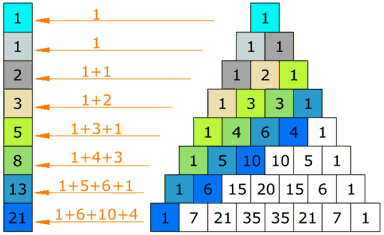
6) Προσθέτοντας τους αριθμούς όπως φαίνεται στο σχήμα θα πάρουμε την γνωστή ακολουθία Fibonacci
7) Αν χρωματίσουμε τους άρτιους και τους περιττούς με διαφορετικά χρώματα θα πάρουμε ένα τρίγωνο όμοιο με αυτό του Sierpinski

Χρήσεις
Το τρίγωνο του Pascal εξαιτίας αυτών των ιδιοτήτων έχει διάφορες χρήσεις.
1) Χρησιμοποιώντας το τρίγωνο μπορούμε να βρούμε τους τριγωνικούς αριθμούς ώστε να κατασκευάσουμε ένα τρίγωνο.
2) Μπορούμε να υπολογίσουμε αναπτύγματα:

Ένα βίντεο που εξηγεί αναλυτικά την παραπάνω χρήση:
*Ένας αριθμός ονομάζεται τριγωνικός όταν ισούται με το άθροισμα ορισμένων διαδοχικών ακεραίων αριθμών με πρώτο το 1. Για παράδειγμα:
1=1
3=1+2
6=1+2+3
10=1+2+3+4
15=1+2+3+4+5
21=1+2+3+4+5+6
28=1+2+3+4+5+6+7
Ο Πασκάλ θα μας ξαναπασχολήσει σε αυτό το blog καθώς έχει διατυπώσει την πασίγνωστη “Αρχή του Πασκάλ”.
Πηγές: https://www.mathsisfun.com/pascals-triangle.html
https://www.math10.com/en/algebra/probabilities/binomial-theorem/binomial-theorem.html
https://www.mathsisfun.com/algebra/triangular-numbers.html
https://www.statisticshowto.com/pascals-triangle/
https://el.wikipedia.org/wiki/%CE%9C%CF%80%CE%BB%CE%B5%CE%B6_%CE%A0%CE%B1%CF%83%CE%BA%CE%AC%CE%BB




