Οι 16 βασικές ιδιότητες του έτους 2016 σαν αριθμού

1) Δίσεκτο έτος

2) Άθροισμα ψηφίων του 9. Αριθμολογική σημασία: καλοσύνη, γενναιοδωρία, συγχώρεση, μετάνοια, ευγνωμοσύνη, θεραπεία, γενναιοδωρία, μεγαλοψυχία

3) Το 2016 έχει την εξής ιδιότητα: 2016² + 2016³ ισούται με έναν αριθμό που περιέχει όλα τα ψηφία από το 0 έως το 9 από μία φορά!

4) Είναι ο 63ος τριγωνικός αριθμός

5) Το 2016 είναι abundant number( άφθονος  η υπερτέλειος  αριθμός) αφού το άθροισμα των διαιρετών του, πλην του εαυτού του, είναι μεγαλύτερο από τον ίδιο.(Δική μας επεξηγηματική προσθήκη.)

6) 2016 = 2¹⁰ + 2⁹ + 2⁸ + 2⁷ + 2⁶ + 2⁵

7) 2016 = 2⁵ * 3² *7

8)  2016² = 2015·2017 + 1

9)  2016·2018 = 2017² – 1

10) (αφού  1+ 2016·2018 = 2017²  και 1+ 2015·2017 = 2016² , η λύση είναι απλή αν σκεφτείτε τη διαφορά τετραγώνων) (Κατερίνα Καλφοπούλου)

 11) Σε δυαδική μορφή: 11111100000

12) Ρωμαϊκή αρίθμηση MMXVI

13) Πλήθος διαιρετών 36 (1 , 2 , 3 , 4 , 6 , 7 , 8 , 9 , 12 , 14 , 16 , 18 , 21 , 24 , 28 , 32 , 36 , 42 , 48 , 56 , 63 , 72 , 84 , 96 , 112 , 126 ,144 , 168 , 224 , 252 , 288 , 336 , 504 , 672 , 1008 , 2016)

14) Άθροισμα διαιρετών 6552

15) Δεν είναι προφανώς πρώτος αριθμός αλλά σύνθετος (δες ιδιότητα 7), ούτε Fibonacci αριθμός.

16) The number of the beast: 666 + 666 + 666 +(6+6+6)= 2016  (Ανδρέας Σκαπεράς)

Πηγές

1) http://www.numberempire.com/2016

2) http://aboutnumber.ru/2016

3) http://www2.stetson.edu/~efriedma/numbers.html

Το είδαμε :http://lisari.blogspot.gr/

Ο δεκάλογος του δασκάλου κατά τον Bertrand Russell

Οι  δέκα εντολές ενός καλού δάσκαλου από τον μαθηματικό και φιλόσοφο Bertrand Russell,(1872 – 1970).Δημοσιεύτηκε το Δεκέμβριο του 1951 στο The New York Times Magazine σε ένα άρθρο για τον φανατισμό.Περισσότερο επίκαιρες όμως από ποτέ .
1.Μην αισθάνεσαι απόλυτα σίγουρος για αυτό που διδάσκεις .
2.Μην σκέπτεσαι ότι αξίζει να προχωράς κρύβοντας τις αποδείξεις,διότι είναι βέβαιο ότι οι αποδείξεις θα έρθουν στο φως .
3. Να μην προσπαθείς πότε να αποθαρρύνεις την σκέψη επειδή αν το κάνεις είναι σίγουρο ότι θα το πετύχεις .
4.Όταν συναντάς αντίδραση, ακόμη και αν αυτή προέρχεται  από τον ή την σύζυγο σου ή από τα παιδιά σου να πασχίζεις να την ξεπεράσεις με          επιχειρήματα και όχι μέσω της εξουσίας , διότι η νίκη η όποια εξαρτάται από την εξουσία είναι απατηλή.
5. Να μην δείχνεις σεβασμό στην εξουσία  των άλλων, διότι είναι δυνατόν να βρει κάνεις αντίθετες  εξουσίες.
6. Να μην χρησιμοποιείς ισχύ για να φιμώσεις  απόψεις τις οποίες θεωρείς ολέθριες, διότι αν το κάνεις οι απόψεις θα εξαφανίσουν τελικά εσένα.
7.Να μην φοβάσαι αν είσαι εκκεντρικός στις απόψεις σου,διότι κάθε άποψη η οποία είναι αποδεκτή σήμερα κάποτε υπήρξε εκκεντρική.
8.Να βρίσκεις περισσότερη απόλαυση όταν ευφυείς συνομιλητές διαφωνούν μαζί σου από ότι αν παθητικοί συνομιλητές  συμφωνούν μαζί σου ,διότι,αν αξιολογείς την νόηση όπως θα όφειλες η πρώτη περίπτωση υποδηλώνει μια βαθύτερη συμφωνία από την δεύτερη.
9.Να είσαι ενσυνείδητα ειλικρινής ,ακόμη και αν η αλήθεια είναι άβολη,διότι είναι περισσότερο άβολη όταν προσπαθείς να την αποκρύψεις .
10.Να μην ζηλεύεις την ευτυχία εκείνων οι οποίοι βλακωδώς θεωρούν ότι ζουν στον παράδεισο, διότι μόνο ένας βλάκας θα σκεφτεί ότι αυτή είναι η ευτυχία.

Περισσότερα  στο σύνδεσμο:
http://www.brainpickings.org/index.php/2012/05/02/a-liberal-decalogue-bertrand-russell/

Πηγή:http://mathhmagic.blogspot.gr/

Πυθαγόρας – Τα πάντα είναι αριθμοί

Ο Πυθαγόρας πίστευε ότι οι αριθμοί ήταν θείες οντότητες και τους εξίσωνε με τους θεούς. Οι αριθμοί 1 έως 10, η λεγάμενη δεκάδα, είχαν υποτίθεται μια ιδιαίτερη ιερότητα. Όμως, ο Πυθαγόρας, εξισώνοντας τους θεούς με αριθμούς, αναδιάρθρωσε ριζικά το ελληνικό πάνθεον: οι θεοί, όχι πλέον ανθρωπόμορφα όντα σε μια θεϊκή μελοδραματική παράσταση, είχαν γίνει αφηρημένες μαθηματικές οντότητες. Η πυθαγόρεια εικόνα του κόσμου δεν ήταν το συμπαντικό θέατρο του Όμηρου και του Ησίοδου, αλλά ένας μεταφυσικός χορός αριθμών.

Αυτό ωστόσο το αριθμητικό σύμπαν ήταν πλουσιότερο απ’ όσο θα μπορούσαν να φανταστούν τα περισσότερα νεότερα μυαλά, επειδή οι πυθαγόρειοι πίστευαν στα ηθικά χαρακτηριστικά των αριθμών. Έτσι, όπως στην πρώιμη ελληνική μυθολογία, η κοσμολογία τους διατήρησε μια ψυχολογική διάσταση. Σήμερα, βλέπουμε το 4 απλώς σαν μια ποσότητα που μας επιτρέπει να λέμε ότι υπάρχουν τέσσερις εποχές μέσα σ’ ένα χρόνο, ή τέσσερις πλευρές σ’ ένα τετράγωνο. Για εκείνους, όμως, το 4 ήταν κάτι πολύ πιο σημαντικό από αυτό. Ήταν, λόγου χάρη, ο αριθμός της δικαιοσύνης. (Σ.τ.Μ.: Η δικαιοσύνη είναι “τετράγωνος αριθμός” και αργά ή γρήγορα, κάθε αδικία θα “τετραγωνιστεί” με αντίστοιχη τιμωρία.) Το τέσσερα είναι 2 φορές το 2, πράγμα που για εκείνους σήμαινε μια εξισορροπημένη πλάστιγγα. Ομοίως, το 6 ήταν ο αριθμός του γάμου, γιατί το 6 είναι 2 φορές το 3 και θεωρούσαν το 2 ως θηλυκό αριθμό και το 3 ως αρσενικό. Έτσι, το 6 ήταν το πρώτο αρσενικοθηλυκό γινόμενο. Η αντίληψη ότι οι αριθμοί έχουν μη ποσοτικά χαρακτηριστικά, ήταν πιθανότατα μια ακόμη πλευρά της φιλοσοφίας που ο Πυθαγόρας απέκτησε στην Αίγυπτο, γιατί αυτό ήταν χαρακτηριστικό και της αιγυπτιακής αριθμολογίας.

Πα τους πυθαγόρειους, οι μη ποσοτικές ιδιότητες των αριθμών σήμαιναν ότι μπορούσαν να χρησιμεύσουν ως ηθικά αρχέτυπα, και έτσι η μελέτη των μαθηματικών μπορούσε να ρίξει φως στην ανθρώπινη συμπεριφορά. Πάνω απ’ όλα, επειδή οι μονοί αριθμοί θεωρούνταν αρσενικοί και οι ζυγοί θηλυκοί, οι ξέχωρες ιδιότητες μονών και ζυγών είχαν ηθικές σημασίες για αμφότερα τα φύλα. Ιδιαιτέρως, η πυθαγόρεια αντίληψη ότι οι μονοί αριθμοί αντιπροσώπευαν το καλό και οι ζυγοί το κακό, έριξε τις γυναίκες μια για πάντα στην πλευρά του κακού. Βλέπουμε έτσι την ανάδυση της πυθαγόρειας δυαρχίας: από τη μια μεριά στέκονταν οι ιδιότητες του καλού (ευθύτητα και αρρενωπότητα) και από την άλλη οι ιδιότητες του κακού (δολιότητα και θηλυκός φθόνος). Κατά κανόνα, οι ιδιότητες που θεωρούνται ανώτερες ή καλύτερες ήταν από την πλευρά του άρρενος, ενώ αυτές που θεωρούνται κατώτερες ή χειρότερες ήταν από την πλευρά του θήλεος. Σε γενικές γραμμές, το καθήκον του πυθαγόρειου μαθηματικού ήταν να ανακαλύπτει τα χαρακτηριστικά των επιμέρους αριθμών (είτε μονών είτε ζυγών), και τις σχέσεις ανάμεσά τους, τόσο τις αριθμητικές όσο και τις ηθικές. Έτσι, αναπόφευκτα, ο μαθηματικός ήταν ένας σπουδαστής της ηθικής. Ο νεότερος διαχωρισμός ανάμεσα στα μαθηματικά και την ηθική, που τόσο δεδομένο τον θεωρούμε, θα είχε κάνει τον Πυθαγόρα να φρίξει, γιατί ο Πυθαγόρας ήταν από τους πρώτους που κατάλαβαν ότι τα μαθηματικά θα μπορούσαν να εφαρμοστούν στην ανάπτυξη καταστροφικών τεχνολογιών, και από εδώ προκύπτει μια ηθική υπευθυνότητα.

Οι πυθαγόρειοι πίστευαν ότι οι αριθμοί χρησίμευαν όχι μόνον ως ηθικά αρχέτυπα, αλλά και ως αρχέτυπα του υλικού κόσμου. Πράγματι, τους αριθμούς τους έβλεπαν ως μοντέλα για κάθε φυσική μορφή. Η έννοια των αριθμών ως πηγής μορφής προήλθε από την πυθαγόρεια ανακάλυψη ότι ο κάθε αριθμός θα μπορούσε να συσχετιστεί με ξέχωρα σχήματα. Λόγου χάρη, το 6, το 10 και το 15 ονομάζονταν τρίγωνοι αριθμοί επειδή έξι, δέκα ή δεκαπέντε κουκίδες θα μπορούσαν να διαταχθούν έτσι ώστε να σχηματίσουν ισόπλευρα τρίγωνα.  Ομοίως, το 4, το 9, και το 16 ονομάζονταν τετράγωνοι αριθμοί.

Το δώδεκα το θεωρούσαν “ορθογώνιο” αριθμό, επειδή θα μπορούσε να συγκροτηθεί από τρεις σειρές με τέσσερις κουκίδες και επίσης από δύο σειρές με έξι κουκίδες. Ορισμένοι αριθμοί, όπως το 6 (που είναι και τριγωνικός και “ορθογώνιος”), θα μπορούσαν να πάρουν περισσότερα του ενός σχήματα. Οι κουκίδες θα μπορούσαν να τοποθετηθούν σε όποιο σχήμα θα διάλεγε κανείς: σε πεντάγωνα, σε εξάγωνα, σε οκτάγωνα και λοιπά.

Ο Πυθαγόρας υποστήριζε ότι αν οι αριθμοί είχαν μορφές, τότε ίσως, αντίστροφα, όλες οι μορφές θα μπορούσαν να συσχετιστούν με αριθμούς. Στ’ αλήθεια, θα μπορούσε άραγε ο αριθμός να είναι η ουσία της ίδιας της μορφής; Ένα απλό παράδειγμα συσχετισμού ενός αριθμού από κουκίδες με ένα περίπλοκο σχήμα θα μπορούσε να δει κανείς στους αστερισμούς. Εδώ, ένα σχήμα από μισή ντουζίνα περίπου φωτεινά σημεία έγινε κριός, ταύρος, κάβουρας ή άνθρωπος. Μερικοί ιστορικοί υποστήριξαν ότι ο Πυθαγόρας ίσως συνέλαβε τους αριθμούς ως την ουσία της μορφής λόγω των εμπειριών που απέκτησε ζώντας ανάμεσα σε αστρονόμους της Βαβυλώνας.

Οι Πυθαγόρειοι, χρησιμοποιώντας σχέδια με κουκίδες, ανακάλυψαν μαθηματικά θεωρήματα εκπληκτικής συνθετικότητας. Επιπλέον, μολονότι οι μαθηματικοί σε μεταγενέστερους αιώνες θα χρησιμοποιούσαν πολύ πιο περίτεχνες τεχνικές, η ιδέα ότι η μορφή είναι κατ’ ουσίαν μαθηματική αποδείχτηκε εξαιρετικά καρποφόρα. Οι μαθηματικοί δεν έχουν πια να κάνουν με διάταξη κουκίδων. Αντίθετα, προσπαθούν να αποδώσουν τη μορφή μέσα από εξισώσεις. Λόγου χάρη, ένας κύκλος μπορεί να αποδοθεί με την απλή εξίσωση x2+y2=r2 (όπου χ και y είναι οι αποστάσεις σ’ έναν οριζόντιο και έναν κάθετο άξονα, και r η ακτίνα του κύκλου). Μια παραλλαγή αυτής της εξίσωσης απεικονίζει μια έλλειψη, η οποία, στην πραγματικότητα, είναι ένας επιμήκης κύκλος. Αποδεικνύεται έτσι ότι οι τροχιές των πλανητών γύρω από τον ήλιο παίρνουν τη μορφή ελλείψεων, όπως η τροχιά της σελήνης γύρω από τη γη. Μία και μόνη λοιπόν εξίσωση (ένας μαθηματικός τύπος) εκφράζει το χορό του ηλιακού συστήματος.

Οι πυθαγόρειοι παρατήρησαν ότι οι αριθμοί είναι εμφανείς όχι μόνο σε χωρικά αλλά και σε χρονικά πρότυπα. Ο κάθε χρόνος αποτελείται από 4 εποχές, 13 σεληνιακούς μήνες, ή 365 μέρες. Ο ήλιος ανατέλλει και δύει σ’ ένα κανονικό κύκλο 24 ωρών, η σελήνη “γεμίζει” και “αδειάζει” κάθε 29 μέρες και ο κάθε πλανήτης έχει το δικό του μοναδικό ρυθμό. Έτσι, το σύμπαν μπορεί να φαντάζει στα μάτια μας σαν μια μεγαλειώδης σειρά αριθμητικών κύκλων. Τα χρονικά αριθμητικά πρότυπα που είναι εμφανή στον ουρανό και τα καμωμένα από αριθμούς χωρικά πρότυπα, έπεισαν τον Πυθαγόρα ότι τα πάντα, στην πραγματικότητα, ήταν αριθμοί (Σ.τ.Μ.: αριθμώ δε τε πάντ’ επέοικεν, Ιάμβλ. XXXIX, 162), και ότι ο αριθμός ήταν πράγματι η ουσία της αλήθειας.

Για τον Πυθαγόρα, και αυτό είχε τεράστια σημασία, η ανθρώπινη ψυχή ήταν μέρος του μεγάλου αριθμητικού προτύπου του σύμπαντος, επειδή πίστευε ότι όλοι μας μετενσαρκωνόμαστε κάθε 216 χρόνια. Ο αριθμός 216, γνωστός ως ψυχογονικός κύβος, είχε μια ειδική σημασία, μια και ήταν το 6 εις τον κύβο, ή 6 x 6 x 6. Πα τους πυθαγόρειους, αυτό συμβόλιζε την κυκλική επαναφορά, την έννοια ότι όλα τα πράγματα επαναλαμβάνονται. Όπως οι ινδουϊστές, έτσι και οι Πυθαγόρειοι πίστευαν ότι ήταν μοιραίο να υποταχθούν σ’ έναν ατελείωτο κύκλο ζωής μετά τη ζωή, και έτσι τις ψυχές, όπως και τους ίδιους τους αριθμούς, τις θεωρούσαν αθάνατες. Στην πραγματικότητα, η αθανασία της ψυχής και ο ατέρμων μετεμψυχωτικός της κύκλος ήταν τα πρώτιστα θρησκευτικά δόγματα του πυθαγορισμού -η μια πλευρά όπου γινόταν πασιφανής και πάλι η επίδραση της Ανατολής.

Επειδή η ψυχή βρισκόταν σε διαρκή μετενσάρκωση, κατά τον Πυθαγόρα, περνούσε ένα χρονικό διάστημα στη γη (δέσμια σ’ ένα σώμα) και ένα χρονικό διάστημα εκτός γης (ασώματη, άυλη). Έτσι, προέκυψε το ερώτημα: όποτε η ψυχή δεν είναι ενσαρκωμένη, πού ακριβώς περνά τον καιρό της και τι ακριβώς κάνει; Η απάντηση του Πυθαγόρα ήταν ότι έμενε στο ουράνιο βασίλειο των άυλων αριθμών-θεών, όπου απολάμβανε μακάρια τις μελωδίες της μαθηματικής μουσικής του σύμπαντος, της αποκαλούμενης και αρμονίας των σφαιρών. … οι πυθαγόρειοι θεωρούσαν το άκουσμα της αρμονίας των σφαιρών ως τα Θεοφάνια της ανθρώπινης εμπειρίας. Μολονότι ο κάθε άνθρωπος θα μπορούσε να προσδοκά μετά θάνατον αυτή τη θεία απόλαυση, οι πυθαγόρειοι είχαν ως στόχο να απελευθερώσουν τις ψυχές τους για να δοκιμάσουν αυτή την ευδαιμονία ενόσω ακόμα ήταν ζωντανοί. Ο πυθαγορισμός λοιπόν ήταν πρωτίστως μια θρησκεία μετουσίωσης της ψυχής, στην οποία ο σκοπός ήταν να χρησιμοποιηθούν τα μαθηματικά ως εργαλείο για να απελευθερωθεί η ψυχή από το σώμα ώστε να μπορέσει να ανέβει και να μπει στο “ουράνιο” βασίλειο των αριθμών. Τα μαθηματικά, ήταν έτσι μια θρησκευτική προπάντων δραστηριότητα.

Από το βιβλίο “Το παντελόνι του Πυθαγόρα” – Margaret Wertheim

Το είδαμε στο antikleidi.com

Διάκριση μαθητή σε μαθηματικό διαγωνισμό

Ο μαθητής της Β Γυμνασίου Ζυγούρης Σπύρος πήρε το δεύτερο βραβείο  στον 1ο Πανελλήνιο Διαγωνισμό Μαθηματικών «Τα Μαθηματικά στα παιχνίδια» που διοργάνωσε το Πρότυπο Πειραματικό Γυμνάσιο Ευαγγελικής Σχολής. Το σχολείο συγχαίρει τον μαθητή .Ακόμη η σύμβουλος μαθηματικών του νομού Πρέβεζας κυρία Αφροδίτη Πανταζή σε τηλεφωνική επικοινωνία της , εξέφρασε τα συγχαρητήρια της προς τον μαθητή την οικογένειά του και το σχολείο μας. Εμείς συμπληρώνουμε ότι όπως έλεγε ο  A.Einstein, αποτελεί μέρος της υπέρτατης τέχνης του παιδαγωγού η αφύπνιση της χαράς της δημιουργίας και γνώσης στους μαθητές του.

Το σχολείο μας θα συνεχίσει να κινείται προς αυτή την κατεύθυνση.

Διαβάστε εδώ τα   αποτελέσματα του διαγωνισμού.

 

 

ΣΥΜΜΕΤΡΙΑ

Ψηφιακή αφίσα συμμετρικών σχημάτων

ΣΥΜΜΕΤΡΙΑ

Η λέξη προέρχεται από την αρχαία ελληνική λέξη σύμμετρος, που σημαίνει με μέτρο, με κανόνα, με υπολογισμό, με μέτρηση.

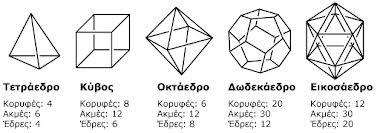
Είναι μία σχέση αναλογίας, συνδεδεμένη με την αρμονία, την ομορφιά και την ολότητα. Τα πλατωνικά στερεά ήταν τέτοιες γεωμετρικές απεικονίσεις «τέλειων» σχέσεων. Ο Κέπλερ βάσισε τη θεωρία του για την κίνηση των ουράνιων σωμάτων στη θεωρία των πλατωνικών στερεών.

Τα πλατωνικά στερεά

Ο Αριστοφάνης στο Συµπόσιο του Πλάτωνα αφηγείται µια διαφορετική ιστορία για το πως προήλθε η αµφίπλευρη από τη σφαιρική συµµετρία και ερμηνεύει τον Έρωτα. Αρχικά ο άνθρωπος ήταν στρογγυλός µε δύο πρόσωπα που το καθένα έπιανε τη μία πλευρά του κεφαλιού του. Για να ταπεινώσει την υπερηφάνεια και την δύναµη του ανθρώπου, ο ∆ίας άρχισε να τους κόβει στα δύο. Έρωτας, κατά τον αρχαίο Έλληνα ποιητή είναι ο πόθος μας να ενωθούμε ξανά σε ένα πλήρες ον, μία τέλεια συμμετρική σφαίρα.

Η ελληνική λέξη που ταξιδεύει στον κόσμο 2.500 χρόνια

Αγγλικά – symmetry

Αλβανικά Ινδονησιακά – simetri

Γαλλικά, Τσέχικα – symetrie

Γερμανικά , Ολλανδικά – symmetrie

Δανικά, Νορβηγικά – symmetri

Λατινικά – symmetria

Ιρλανδικά – simeadrachta

Ισπανικά, Γαλικιακά, Βασκικά, Πορτογαλικά – simetria

Ιταλικά – simmetria

Κροάτικα – simetrija

Μαλτέζικα – simetrija

Αφρικάνικα – simmetrie

Βουλγαρικά –симетрия

Ρώσικα – симметрия

Αναστασία Παπανίκα

Μαθήτρια της Α΄ Γυμνασίου

Ακολουθούν, οι εργασίες των μαθητών της Α΄Γυμνασίου του Δέσκειου Γυμνασίου Πάργας.