
Διακρίνουμε δύο περιπτώσεις:

Παράδειγμα 1°:
Μια σημειακή μάζα Σ είναι δεμένη στο άκρο Α αβαρούς ράβδου, μήκους L, η οποία μπορεί να στρέφεται σε κατακόρυφο επίπεδο χωρίς τριβές, γύρω από οριζόντιο άξονα που περνά περνά από το άλλο της άκρο Ο. Σε μια στιγμή μια σφαίρα που κινείται οριζόντια συγκρούεται με με το σώμα Σ.

Ποια η ελάχιστη ταχύτητα του σώματος Σ, αμέσως μετά την κρούση, ώστε να κάνει ανακύκλωση; Δίνεται η επιτάχυνση της βαρύτητας g.
Απάντηση:

Έστω υ0 η ταχύτητα που αποκτά το σώμα Σ αμέσως μετά την κρούση. Για να μπορέσει να διαγράψει τον κατακόρυφο κύκλο του σχήματος, αρκεί η ταχύτητά του στην ανώτερη θέση (2) να ικανοποιεί την σχέση υ2 ≥ 0 και οριακά υ2=0.
Μεταξύ των θέσεων (1) και (2) η μηχανική ενέργεια παραμένει σταθερή και θεωρώντας την θέση (1) σαν επίπεδο μηδενικής ενέργειας έχουμε:

Παράδειγμα 2°:
Μια σημειακή μάζα Σ m είναι δεμένη στο άκρο Α ομογενούς ράβδου μάζας Μ και μήκους L, η οποία μπορεί να στρέφεται σε κατακόρυφο επίπεδο χωρίς τριβές, γύρω από οριζόντιο άξονα που περνά περνά από το άλλο της άκρο Ο. Σε μια στιγμή μια σφαίρα που κινείται οριζόντια συγκρούεται με με το σώμα Σ.

Ποια η ελάχιστη ταχύτητα του σώματος Σ, αμέσως μετά την κρούση, ώστε να κάνει ανακύκλωση;
Δίνεται η επιτάχυνση της βαρύτητας g και η ροπή αδράνειας της ράβδου ως προν τον άξονα περιστροφής της Ι= 1/3 ΜL2.
Απάντηση:
Έστω υ0 η ταχύτητα που αποκτά το σώμα Σ αμέσως μετά την κρούση. Για να μπορέσει να διαγράψει τον κατακόρυφο κύκλο του σχήματος, αρκεί η ταχύτητά του στην ανώτερη θέση (2) να ικανοποιεί την σχέση υ2 ≥ 0 και οριακά υ2=0.

Μεταξύ των θέσεων (1) και (2) η μηχανική ενέργεια παραμένει σταθερή και θεωρώντας την θέση (1) σαν επίπεδο μηδενικής ενέργειας έχουμε:
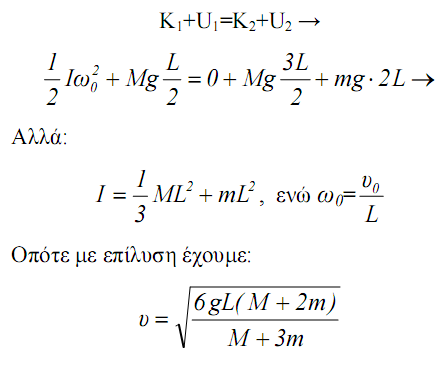

Και ποια είναι αυτή η ταχύτητα;
Α) Έστω ότι το σώμα, που το θεωρούμε υλικό σημείο, είναι δεμένο στο άκρο νήματος και διαγράφει κατακόρυφο κύκλο.

Για την ανώτερη θέση έχουμε:

Από την παραπάνω σχέση προκύπτει ότι όταν μειώνεται η ταχύτητα του σώματος, μειώνεται και η τάση του νήματος. Η ελάχιστη τιμή της ταχύτητας, στην θέση αυτή, θα είναι εκείνη για την οποία Τ=0. Δηλαδή η ταχύτητα για την οποία το βάρος του σώματος παίζει τον ρόλο της κεντρομόλου. Έτσι:

Αυτό είναι το μέτρο της ελάχιστης ταχύτητας που πρέπει να έχει το σώμα στην ανώτερη θέση.
Β) Έστω μια σφαίρα, ακτίνας r, που κινείται διαγράφοντας κατακόρυφο οδηγό ακτίνας R, όπως στο σχήμα και υ η ταχύτητα του κέντρου της (ταχύτητα κέντρου μάζας της σφαίρας).
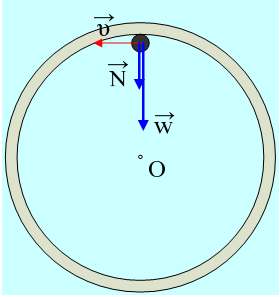
Για την ανώτερη θέση έχουμε:

Από την παραπάνω σχέση προκύπτει ότι όταν μειώνεται η ταχύτητα του σώματος, μειώνεται και η κάθετη αντίδραση του επιπέδου Ν. Η ελάχιστη τιμή της ταχύτητας, στην θέση αυτή, θα είναι εκείνη για την οποία Ν=0. Δηλαδή η ταχύτητα για την οποία το βάρος του σώματος παίζει τον ρόλο της κεντρομόλου. Έτσι:

Αυτό είναι το μέτρο της ελάχιστης ταχύτητας που πρέπει να έχει το σώμα στην ανώτερη θέση.
Η ακτίνα της σφαίρας είναι αμελητέα, R-r ≈ R και η σχέση μπορεί να γραφτεί:

Προσέξτε ότι και στις δύο παραπάνω περιπτώσεις το αποτέλεσμα είναι το ίδιο.
Μπορείτε να το κατεβάσετε σε pdf.
Καλή δουλειά, που λείπει απο τα σχολικά βιβλία,
…αλλά,
1. με τον όρο ανακύκλωση δεν εννοούμε τη συνθήκη…, αλλά τη πραγματοποίηση κατακόρυφης κυκλικής τροχιάς απο ένα σώμα (η συνθήκη, που συνήθως ζητείται, είναι η συνθήκη ώστε να…)
2. για την ομογένεια της παρουσίασης των δύο περιπτώσεων, (επειδή συνήθως ζητείται η ταχύτητα κάτω), αν “προχωρήσει” λίγο η περίπτωση 2 θα προκύψει οτι η ελάχιστη ταχύτητα του σώματος (κάτω) είναι ίση με τετραγωνική ρίζα πέντε επί την ελάχιστη ταχύτητα (πάνω) που σωστά έχει υπολογισθεί.
1. με τον όρο ανακύκλωση δεν εννοούμε τη συνθήκη…, αλλά τη πραγματοποίηση κατακόρυφης κυκλικής τροχιάς απο ένα σώμα (η συνθήκη, που συνήθως ζητείται, είναι η συνθήκη ώστε να…)
Έχετε απόλυτα δίκιο, αλλά δεν πρόλαβα να κάνω την διόρθωση στο Blog αυτό, αλλά μόνο στο blogspot!!!
Δυστυχώς με προλάβατε!!!