Γιατί το ουράνιο τόξο έχει σχήμα κυκλικού τόξου;

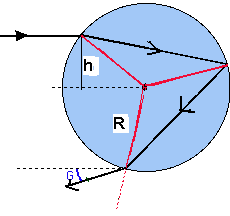
Είναι γνωστό ότι το ουράνιο τόξο σχηματίζεται όταν ο παρατηρητής έχει πίσω του τον ήλιο και οι ακτίνες του ήλιου παθαίνουν δύο διαθλάσεις και μια ανάκλαση στις σταγόνες της βροχής που βρίσκονται μπροστά από τον παρατηρητή. Γιατί όμως το σχήμα του είναι κυκλικό τόξο; και από τί εξαρτάται το μήκος του τόξου που παρατηρούμε;

Αν σχεδιάσουμε την πορεία μιας ακτίνας του ήλιου που προσπίπτει επί μιας σφαιρικής σταγόνας βροχής και παθαίνει διαδοχικά, μια διάθλαση καθώς εισέρχεται στην σταγόνα, μια ανάκλαση στο πίσω μέρος της σταγόνας και μια διάθλαση πάλι στο εμπρόσθιο μέρος της σταγόνας για να φτάσει στη συνέχεια στα μάτια του παρατηρητή. (Βλέπε εικόνα 1)

Εικόνα 1

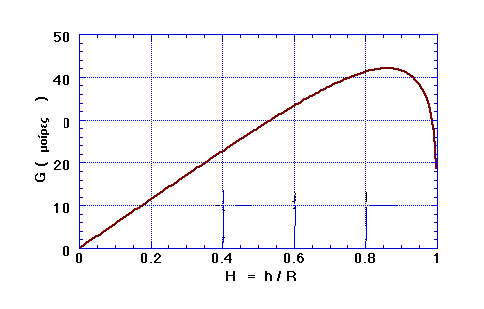
Αν υπολογίσουμε με το νόμο του Snell και τη χρήση τριγωνομετρίας, τη γωνία G, που σχηματίζει η εξερχόμενη ακτίνα από τη σταγόνα, με την διεύθυνση της αρχικής ακτίνας, θα βρούμε ότι η τιμή της γωνίας αυτής εξαρτάται από την παράμετρο πρόσπτωσης, Η = h/R. (Βλέπε εικόνα 1)

Μάλιστα το γράφημα της συνάρτησης G = f(H) φαίνεται στην εικόνα 2. Ως δείκτης διάθλασης για το νερό έχει υποτεθεί η τιμή n=1,33, που αντιστοιχεί στο κόκκινο χρώμα.

Εικόνα 2

Σε οποιοδήποτε πρόβλημα σκέδασης, το μέγιστο της έντασης στη σκεδαζόμενη δέσμη, θα παρατηρηθεί προς εκείνη την κατεύθυνση για την οποία μια μικρή μεταβολή της παραμέτρου  πρόσπτωσης (Η), της ακτίνας επί της σταγόνας, δεν προκαλεί μεγάλη μεταβολή στην απόκλιση της δέσμης, η οποία προσδιορίζεται από την γωνία G.

Έτσι λοιπόν και σε αυτή την περίπτωση της σκέδασης του φωτός από τη σταγόνα με δύο διαθλάσεις και μια ανάκλαση, το μέγιστο της έντασης του φωτός, δηλαδή η μεγαλύτερη λαμπρότητα θα παρατηρηθεί για την τιμή της παραμέτρου Η, για την οποία μια μικρή μεταβολή του Η αφήνει ανεπηρέαστη την τιμή της γωνίας G. Δηλαδή η μέγιστη ένταση φωτός, αντιστοιχεί στο ακρότατο της συνάρτησης G = f(H).

Δηλαδή με άλλα λόγια, το ακρότατο της συνάρτησης G = f(H), αντιστοιχεί στην περίπτωση των πιο πολλών ακτίνων που φτάνουν στο μάτι του παρατηρητή. Έτσι στη συγκεκριμένη γωνία με τιμή περίπου 42⁰ (όπως προκύπτει από το γράφημα), ο παρατηρητής βλέπει το πιο έντονο φως. Προφανώς από το γράφημα προκύπτει ότι και για άλλες τιμές της παραμέτρου πρόσπτωσης που αντιστοιχούν σε γωνίες μικρότερες των 42⁰, ο παρατηρητής βλέπει σκεδαζόμενες ακτίνες, αλλά πολύ αμυδρότερες. Ενώ αντίθετα, για καμιά τιμή της παραμέτρου πρόσπτωσης Η, δεν υπάρχει γωνία εκτροπής G, μεγαλύτερη των 42⁰.

Όλη την παραπάνω ανάλυση είχε κάνει ήδη από τον 17ο αιώνα ο Καρτέσιος.

Εικόνα 3.

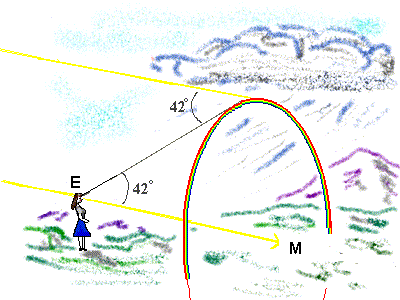
Κάθε σταγόνα όμως είναι σφαιρική, κι έτσι το αποτέλεσμά της πάνω στην πορεία του φωτός του ήλιου είναι συμμετρικό γύρω από έναν άξονα που περνά από το κέντρο της σταγόνας και την πηγή του φωτός (στην προκειμένη περίπτωση τον ήλιο). Όλες λοιπόν οι σταγόνες που βρίσκονται σε κατευθύνσεις οι οποίες σχηματίζουν με την διεύθυνση ΕΜ της παραπάνω εικόνας 3, γωνία 42⁰, μας δίνουν ως αποτέλεσμα της σκέδασης του φωτός ουράνιο τόξο.

Οι σταγόνες αυτές ορίζουν ένα κυκλικό τόξο, τα σημεία του οποίου, όπως φαίνεται και στην εικόνα 3, προσδιορίζουν το σχήμα του ουράνιου τόξου.

Οι σταγόνες που δίνουν ουράνιο τόξο βρίσκονται σε μια κωνική τομή ενός κώνου με τον παρατηρητή στην κορυφή του κώνου και με κωνικό άνοιγμα 84⁰ = (2 Χ 42⁰).

Δεν μπορούμε βέβαια να δούμε ολόκληρο τον κύκλο της κωνικής αυτής τομής διότι παρεμβάλλεται η Γη. Όσο πιο χαμηλά βρίσκεται ο ήλιος στον ορίζοντα, τόσο πιο μεγάλο μέρος αυτού του κυκλικού τόξου βλέπουμε. Αν ο ήλιος βρίσκεται ακριβώς στη Δύση του, θα βλέπαμε ένα πλήρες ημικύκλιο, του ουράνιου τόξου, με την κορυφή του τόξου 42 μοίρες πάνω από τον ορίζοντα.

Όσο πιο ψηλά βρίσκεται ο ήλιος στον ουρανό, τόσο μικρότερο θα είναι το μέρος του ουράνιου τόξου που θα βρίσκεται πάνω από τον ορίζοντα.

Γιατί το κύριο ουράνιο τόξο παρατηρείται πάντα σε συγκεκριμένη γωνία πάνω από τον ορίζοντα;