Λυγάτσικας Ζήνων – Πρότυπο Γ.Ε.Λ. Βαρβακείου Σχολής

• 11) ΠΡΟΒΛΗΜΑ (για το γυμνάσιο) Να βρείτε μια διαδικασία ώστε να επαναλάβετε τη κατασκευή του παρακάτω σχήματος μέχρι το 10^ο τετράγωνο. Αν η πλευρά του μεγάλου τετραγώνου είναι 24 cm, να βρείτε το εμβαδόν του 10^ου τετραγώνου.

Λήψη αρχείου

• 10) Ο Α και ο Β συναντούν μια οικογένεια που αποτελείται από 7 μέλη διαφορετικής ηλικίας μεταξύ τους. Ακολουθεί ο παρακάτω διάλογος:
  Α: Τα μερικά αθρίσματα και το συνολικό άθροισμα των ηλικιών των 7 μελών της οικογένειας, μας επιτρέπει να πάρουμε όλους τους φυσικούς ανάμεσα από 1 και 121 (των ορίων συμπεριλαμβανομένων).  Μπορείς να βρείς την ηλικία των μελών της;
  Β: Η λύση είναι απροσδιόριστη!
  Α: Να ξέρεις ότι είμαι μεγαλύτερος στην ηλικία από τον μεγαλύτερο της οικογένειας.
  Β: Αυτό μου έδωσε λύση στο πρόβλημα.
• Ποιες είναι οι ηλικίες των μελών της οικογένειας και ποιά η ηλικία του Α;
• Δείτε τη λύση: https://zligatsikas.wixsite.com/website  
  

  ---

• 9) Επίσης μια παράξενη ερώτηση: Είναι δυνατόν μια συνάρτηση f: R^d στο R να έχει ένα μη-αριθμήσιμο αριθμό διακεκριμένων τοπικών μεγίστων?

• 8) Ένα  “παράξενο” ολοκλήρωμα του Papanikolaou

Δίνω μια εξήγηση καθώς και την άποψή μου γιατί μου φάνηκε “παράξενο”

• 7) Ένα πρόβλημα για μαθηματικούς διαγωνισμούς. Πάνω σε ιδέα του Lucian Tutesku, άνοιξη του 2018.

Μια υπόδειξη:

Λήψη αρχείου

• 6) To ρολόϊ με τους ίσους δείκτες (Δύσκολο)

Το ρολόϊ της Αλίκης έχει δύο ίσους δείκτες. Πόσες φορές την ημέρα δεν μπορεί να γνωρίζει τι ώρα είναι. (πρόβλημα του David Gontier)

Aπάντηση: Σε λίγο

• 5)
  

Από την Αγγλία, ο Δημήτρης μας έστειλε την λύση, την οποία θα την δημοσιεύσουμε σύντομα.

• 4)

Η οικογένεια Παυλίδου έχει 5 παιδιά. Τα μισά είναι κορίτσια. Πως το εξηγείται αυτό; (Δεν μετράν οι γονείς, και όλα τα παιδιά είναι είτε πραγματικά αγόρια είτε πραγματικά κορίτσια, μην πάει το μυαλό σας αλλού, πονηροί!)

Ένας συνάδελφος από τον Νομό Φβιώτιδας μας έστειλε την λύση: Και τα άλλα μισά είναι και αυτά κορίτσια. Άρα, έχει 5 κορίτσια!

• 3)

Tα κομμάτια της πρώτης εικόνας έχουν ενωθεί διαφορετικά στην δεύτερη, αλλά περίσσεψαν δυο μικρά τετράγωνα στο κέντρο. Τι έχει συμβεί στην πραγματικότητα;

Ένας μαθητής από την Ρόδο μας έστειλε την παρακάτω υπόδειξη που οδηγεί στην λύση! Σημεία που φαίνονται συνευθειακά στην πραγματικότητα δεν είναι. Αν προσπαθήσετε να κατασκευάσετε το σχήμα σε ένα σύστημα δυναμικής γεωμετρίας, θα το δείτε.

• 2)

Μπορείτε να βρείτε την επόμενη σειρά με τους αριθμούς?

1
11
21
1211
111221
312211

……….

Μπορείτε να δείξετε ότι αυτή δεν μπορεί να περιέχει το 4?

O Δημήτρης έστειλε την σωστή απάντηση:
Καταρχάς λαμβάνουμε κάθε ψηφίο σαν έναν ξεχωριστό αριθμό.

Κάθε σειρά περιγράφει με αριθμούς ότι βλέπουμε στην από πάνω σειρά πχ η πρώτη σειρά έχει ένα 1. Άρα η από κάτω θα είναι η 11. Τώρα η δεύτερη σειρά έχει δύο 1. Επομένως στην τρίτη σειρά γράφουμε 21. Η τρίτη σειρά τώρα έχει ένα 2 και ένα 1. Αρα στην τέταρτη σειρά γράφουμε 1211 κοκ
Με τον ίδιο τρόπο κάτω από την τελευταία σειρά γράφω: ένα 3, ένα 1, δύο 2 και δύο 1 δηλαδή 13112221.
Το 4 δεν μπορεί να περιέχεται σε καμιά γραμμή διότι για να εμφανιστεί πρέπει να έχουμε στην από πάνω γραμμή 4 ίδιους αριθμούς. Όμως το maximun ίδιων αριθμών που μπορούν να εμφανιστούν συνεχόμενοι είναι 3 (μόνο αν στην από πάνω σειρά περιέχονται συνεχόμενα ο α α-φορές και ο β α-φορές έτσι ώστε από κάτω να γράψω αααβ).

• 1) Αίνιγμα Γεωμετρίας

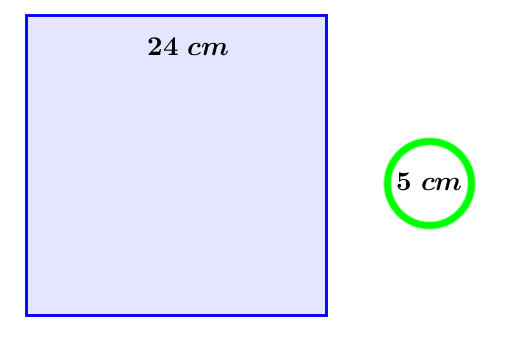
Δίνεται ένα τετράγωνο με πλευρά ίση με 24 cm και ένα δακτυλίδι διαμέτρου 5 cm. Να κόψετε το τετράγωνο σε τέσσερα ίσα κομμάτια τα οποία να μπορούν να διέλθουν από το εσωτερικό του δακτυλιδιού χωρίς να σπάσουν.

————————————————————————————

RSS Σχόλιων