📢 Ενδοσχολική Επιμόρφωση στα Μαθηματικά 🧮
📌 Θέμα: Τα Μαθηματικά μέσα από τις δραστηριότητες – Μελέτη περίπτωσης: Το παιχνίδι 🎲
👨🏫 Εισηγητής: Ιωάννης Ρίζος
📍 Θέση: Εντεταλμένος Διδάσκων & Μεταδιδακτορικός Ερευνητής
🏛 Ίδρυμα: Πανεπιστήμιο Θεσσαλίας – Τμήμα Μαθηματικών
📚 Ημερομηνία & Τοποθεσία:
📍 10ο Πειραματικό Σχολείο
🎯 Στόχοι Επιμόρφωσης
🔹 Διερεύνηση της σχέσης μεταξύ μαθηματικών & παιχνιδιού 🧩
🔹 Καινοτόμες διδακτικές προσεγγίσεις για ενεργή συμμετοχή των μαθητών 🏫
🔹 Ανάπτυξη κριτικής σκέψης & δεξιοτήτων μέσω της αλληλεπίδρασης 🎯
✅ Δημιουργία επαγγελματικής κοινότητας μάθησης 👥
✅ Αλληλεπίδραση & ανταλλαγή απόψεων μεταξύ εκπαιδευτικών 🗣️
✅ Συζήτηση & δημιουργικός προβληματισμός 🤔
✅ Μοιραζόμαστε πρακτικές & εμπειρίες 📚
📌 Μια μοναδική ευκαιρία για τους εκπαιδευτικούς να εξερευνήσουν δημιουργικούς τρόπους διδασκαλίας των μαθηματικών! 🚀
🗓️ Πρόγραμμα Συναντήσεων
📌 1η Συνάντηση – 12/3 📊
🔹 Θέμα: Αριθμοί
🔸 Μαθηματικό υπόβαθρο 🔢
🔸 Συνηθισμένα λάθη & δυσκολίες των μαθητών ❌
🔸 Διαχείριση παρανοήσεων & συζήτηση 💡
📌 2η Συνάντηση – 9/4 🎲
🔹 Θέμα: Δραστηριότητες & παιχνίδι
🔸 Διδακτικές προτάσεις ✏️
🔸 Συζήτηση & προοπτικές 📈
🔸 Εισαγωγικό ερώτημα:
“Ποια πιστεύετε ότι είναι τα χαρακτηριστικά ενός καλού δασκάλου των Μαθηματικών;” 👨🏫
📌 Βασικά χαρακτηριστικά ενός καλού δασκάλου Μαθηματικών
📍 Βαθιά γνώση του αντικειμένου 🏛️
📍 Παιδαγωγική γνώση του περιεχομένου 📘
📍 Γνώση του Προγράμματος Σπουδών & σχολικού βιβλίου 📖
📢 Μια μοναδική ευκαιρία για τους εκπαιδευτικούς να εξερευνήσουν νέες προσεγγίσεις στη διδασκαλία των μαθηματικών! 🚀
✅ Οι αριθμοί και η εκπαίδευση
Η διδασκαλία των πραγματικών αριθμών γίνεται σταδιακά στην Πρωτοβάθμια και Δευτεροβάθμια Εκπαίδευση, ακολουθώντας μια σπειροειδή προσέγγιση. Το σύνολο των πραγματικών αριθμών διαμορφώνεται μέσα από βασικά υποσύνολα που εμπλουτίζονται με πράξεις και ιδιότητες.
❓ Η έννοια του αριθμού
Η έννοια του αριθμού, αν και φαίνεται απλή, είναι μία από τις πιο θεμελιώδεις αλλά και πιο σύνθετες μαθηματικές έννοιες. Η θεμελίωσή της ξεκινά από τον Ευκλείδη και τους Πυθαγόρειους, ενώ φτάνει ως τις τομές Dedekind.
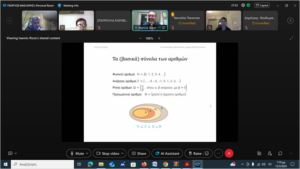
📝 Τα βασικά σύνολα αριθμών
Οι αριθμοί διακρίνονται σε:
- Φυσικούς (0, 1, 2, 3…)
- Ακέραιους (…-2, -1, 0, 1, 2…)
- Ρητούς (εκφράζονται ως κλάσματα π.χ. 1/2, 3/4)
- Άρρητους (π.χ. , )
- Πραγματικούς (όλοι οι παραπάνω)
⚠️ Δυσκολίες των μαθητών στους ρητούς αριθμούς
Έρευνες δείχνουν ότι οι μαθητές αντιμετωπίζουν σημαντικές δυσκολίες με τους ρητούς αριθμούς, οι οποίες ξεκινούν από το Δημοτικό και συνεχίζονται έως το Πανεπιστήμιο.
Κάποιες από τις πιο κοινές παρανοήσεις περιλαμβάνουν:
- 📈 Η αυθαίρετη επέκταση ιδιοτήτων των φυσικών αριθμών στους ρητούς.
- Π.χ. «Ο προηγούμενος αριθμός του 5 είναι το 4,999…»
- ❌ Λανθασμένες αντιλήψεις για τον πολλαπλασιασμό και τη διαίρεση
- Π.χ. «Όταν ένας αριθμός πολλαπλασιάζεται, μεγαλώνει.» (Δεν ισχύει για αριθμούς μεταξύ 0 και 1)
- 📊 Παρανοήσεις λόγω διακριτότητας και πυκνότητας των αριθμών.
- Π.χ. «Ανάμεσα στο 0,4 και 0,5 δεν υπάρχουν άλλοι δεκαδικοί αριθμοί.»
- 📅 Προτεραιότητα δεκαδικών αριθμών έναντι των κλασμάτων
- Οι μαθητές βλέπουν τα κλάσματα ως διαδικασία και όχι ως αριθμητικό αποτέλεσμα.
❗ Προβλήματα με ρητούς και άρρητους αριθμούς
Οι μαθητές δυσκολεύονται:
- Να ορίσουν με ακρίβεια τους ρητούς και άρρητους αριθμούς.
- Να κατανοήσουν τη σχέση πυκνότητας και διευθέτησης στην αριθμογραμμή.
- Να τους τοποθετήσουν σωστά στην αριθμογραμμή.
- Π.χ. «Πού τοποθετούμε το και το 0,333…;»
📃 Προτεινόμενες δραστηριότητες
- Μετατροπή δεκαδικών σε κλάσματα και το αντίστροφο.
- Π.χ. ,
- Ακριβής τοποθέτηση στην αριθμογραμμή
- Π.χ. 0,7, 1/2, 2,25, 1/5, 1/3
- Διασύνδεση με τη Γεωμετρία
- Π.χ. «Μπορούμε να κατασκευάσουμε τετράγωνο διπλάσιου εμβαδού από ένα άλλο;»
🔮 Αξιοποίηση της Ιστορίας των Μαθηματικών
- Ο λόγος της διαγωνίου προς την πλευρά τετραγώνου είναι άρρητος αριθμός.
- Ο λόγος της περιμέτρου προς τη διάμετρο του κύκλου () είναι άρρητος αλλά προσεγγίζεται με ρητούς.
Συμπέρασμα: Η βαθιά κατανόηση των αριθμών και των ιδιοτήτων τους είναι κρίσιμη για την ανάπτυξη μαθηματικής σκέψης. Η ενδοσχολική επιμόρφωση μπορεί να συμβάλει στη βελτίωση της διδασκαλίας και να βοηθήσει τους μαθητές να ξεπεράσουν κοινές μαθηματικές παρανοήσεις! Μέσα από κατάλληλες διδακτικές προσεγγίσεις, οι μαθητές μπορούν να αποκτήσουν μια ουσιαστική κατανόηση των αριθμών, να αναπτύξουν την ικανότητα κριτικής σκέψης και να αξιοποιήσουν τις μαθηματικές έννοιες σε πραγματικά προβλήματα. Η επένδυση στη συνεχή επιμόρφωση των εκπαιδευτικών αποτελεί κλειδί για την ενίσχυση της μαθηματικής παιδείας και την καλλιέργεια θετικής στάσης απέναντι στα μαθηματικά.